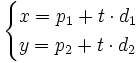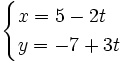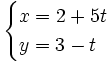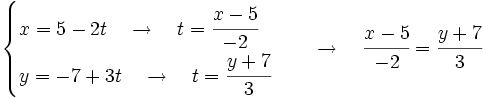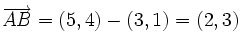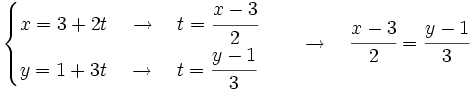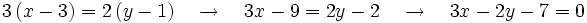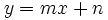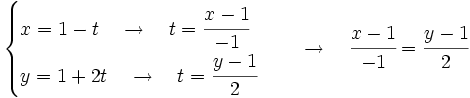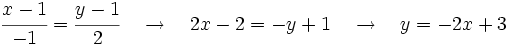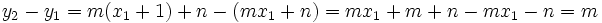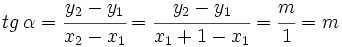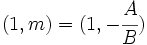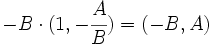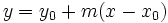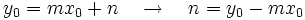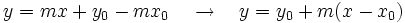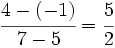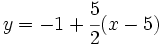Ecuaciones de una recta en el plano (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
(Pág. 191)
Introducción
Ecuaciones de la recta. Condiciones para determinar una recta. Esquema de los tipos de ecuaciones
En esta escena podrás ver las distintas ecuaciones de la recta.
Vector de dirección de una recta
- Una recta
 queda determinada por un punto
queda determinada por un punto  y un vector
y un vector 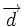 que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
- Dos puntos
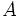 y
y 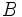 de una recta determinan un vector de dirección de la misma,
de una recta determinan un vector de dirección de la misma, 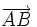 .
.
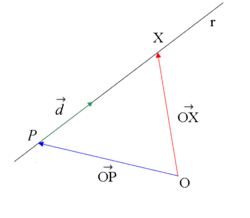
En esta escena podrás ver como un punto del plano y un vector director determinan una recta.
En esta escena podrás ver como dos puntos del plano determinan una recta.
Ecuación vectorial de la recta
Ecuación vectorial de la recta. Ejemplos.
Ecuación vectorial de la recta.
Ejercicios sobre la ecuación vectorial de la recta.
En esta escena podrás ver como se representa la ecuación vectorial de una recta en el plano.
Ecuaciones paramétricas de la recta
Ecuaciones paramétricas de la recta con vector de dirección 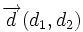 y que pasa por el punto
y que pasa por el punto 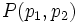 .
.
|
|
A partir de la ecuación verctorial de la recta
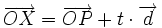
si sustituimos cada vector por sus coordenadas, tenemos:
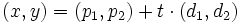
Ejemplo: Ecuaciones paramétricas de la recta
Halla las ecuaciones paramétricas de la recta con vector director 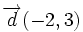 que pasa por el punto
que pasa por el punto 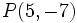 .
.
Ecuaciones paramétricas de la recta. Ejemplos.
Ecuaciones paramétricas de la recta
Ejercicios sobre las ecuaciones paramétricas de la recta
En esta escena podrás ver como se representan las ecuaciones paramétricas de una recta en el plano.
Ecuación continua de la recta
Ecuación continua de la recta con vector director 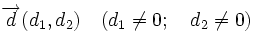 y que pasa por un punto
y que pasa por un punto 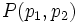 :
:
|
|
A partir de las ecuaciones paramétricas de la recta, despejando el parámetro 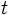 (siempre y cuando las dos coordenadas del vector
(siempre y cuando las dos coordenadas del vector 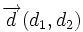 sean distintas de cero), tenemos:
sean distintas de cero), tenemos:
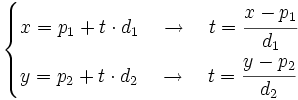
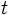 , obtenemos la ecuación.
, obtenemos la ecuación.Ejemplo: Ecuación continua de la recta
Halla la ecuación continua de la recta con vector director 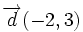 que pasa por el punto
que pasa por el punto 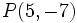 .
.
De las ecuaciones paramétricas despejamos el parámetro 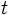 e igualamos:
e igualamos:
Ecuación continua de la recta. Ejemplos.
Ecuación continua de la recta
Ejercicios sobre la ecuación continua de la recta
Ecuación implícita o general de la recta
Ecuación implícita o general de la recta:
|
|
Partiendo de la ecuación continua de la recta: (suponemos que 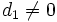 y
y 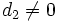 )
)
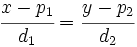
Multiplicando en cruz:
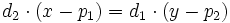
y pasando todos los términos a la izquierda de la ecuación, tenemos:
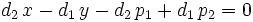
de donde, haciendo: 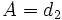 ,
, 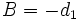 y
y 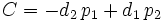
se tiene la ecuación.
Antes hemos supuesto 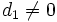 y
y 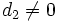 . Si, por el contrario, alguno fuera cero tendríamos:
. Si, por el contrario, alguno fuera cero tendríamos:
- Si
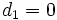 , las ecuaciones paramétricas serían:
, las ecuaciones paramétricas serían:
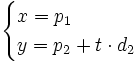
de donde se tiene que la recta es vertical con ecuación 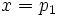 y su ecuación implícita sería
y su ecuación implícita sería 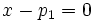 .
.
- Si
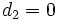 , las ecuaciones paramétricas serían:
, las ecuaciones paramétricas serían:
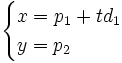
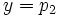 y su ecuación implícita sería
y su ecuación implícita sería 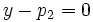 .
.Ejemplo: Ecuación implícita de la recta
Halla la ecuación implícita de la recta que pasa por los puntos 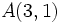 y
y 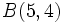 .
.
Primero calculamos su vector de dirección:
Obtenemos las ecuaciones paramétricas con ese vector director y con uno de los dos puntos, por ejemplo 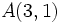 . A partir de éstas obtenemos la ecuación continua:
. A partir de éstas obtenemos la ecuación continua:
Multiplicando en cruz y pasando todos los términos a la izquierda de la ecuación, obtenemos la ecuación implícita:
Proposición
Dada una recta de ecuación 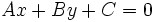 :
:
- El vector
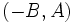 es un vector de dirección de la recta.
es un vector de dirección de la recta.
- El vector
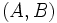 es un vector perpendicular a la recta que se denomina vector normal a la recta.
es un vector perpendicular a la recta que se denomina vector normal a la recta.
Antes vimos, en la deducción de la ecuación explícita, que partiendo de la ecuación continua y haciendo 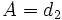 ,
, 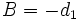 y
y 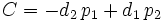 , se tenía la ecuación implícita
, se tenía la ecuación implícita 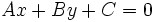 .
.
Entonces, el vector 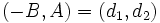 , que es el vector director de la recta
, que es el vector director de la recta
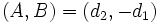 es perpendicular a la recta porque
es perpendicular a la recta porque 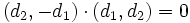 , y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.
, y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.Ecuación general de la recta. Ejemplos.
Ecuación general de la recta
Ejercicios sobre la ecuación general de la recta
Ecuación explícita de la recta
Ecuación explícita de la recta:
|
|
donde  se llama pendiente de la recta y
se llama pendiente de la recta y  ordenada en el origen.
ordenada en el origen.
Partiendo de la ecuación implícita
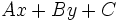
y despejando 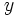 (siempre que
(siempre que 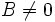 ), tenemos:
), tenemos:
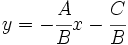
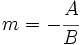 y
y 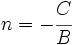 , tenemos la ecuación.
, tenemos la ecuación.Estudio del comportamiento de la recta y=mx+n atendiendo a los parámetros m (pendiente) y n (ordenada en el origen).
Ejemplo: Ecuación explícita de la recta
- Halla la ecuación explícita de la recta de ecuaciones paramétricas:
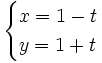
Partimos de las ecuaciones paramétricas y obtenemos su ecuación continua.
Para obtener la ecuación explícita basta con despejar 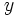 :
:
Proposición
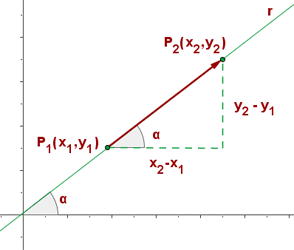
- La pendiente de una recta mide el incremento de la ordenada cuando la abcisa se incrementa en una unidad.
- Si
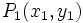 y
y 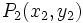 son dos puntos de la recta, entonces su pendiente es
son dos puntos de la recta, entonces su pendiente es 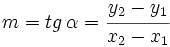
- El vector de coordenadas
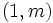 es un vector de dirección de la recta.
es un vector de dirección de la recta.
1. Sean 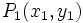 y
y 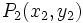 , dos puntos de la rectan y tomemos
, dos puntos de la rectan y tomemos 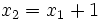 .
.
Sus abcisas 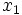 y
y 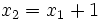 difieren en 1.
difieren en 1.
Veamos sus ordenadas en cuanto difieren:
2. Por la definición de tangente de un ángulo:
3. En la deducción de la ecuación explícita vimos que 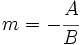 , entonces:
, entonces:
Si multiplicamos ambas coordenadas por 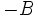 , obtenemos otro vector con la misma dirección:
, obtenemos otro vector con la misma dirección:
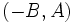 era el vector de dirección de la recta.
era el vector de dirección de la recta.Halla la pendiente de la recta que pasa por los puntos P(1,1) y Q(4,4).
Ecuación explícita de la recta. Ejemplos.
Ecuación explícita de la recta
Ejercicios sobre la ecuación explícita de la recta
Ecuación de la recta que pasa por dos puntos
Sabemos que dos puntos determinan un vector de dirección. Con ese vector de dirección y uno de los dos puntos podemos obtener la ecuación de la recta.
En esta escena podrás ver como se obtiene la ecuación de la recta que pasa por dos puntos.
Ejemplo.
|
Actividad: Ecuación de la recta que pasa por dos puntos
Halla y representa la ecuación de la recta que pasa por los puntos (3,5) y (2,3). Averigua su pendiente y los puntos de corte con los ejes.
Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: line (3,5),(2,3) |
Ecuación punto-pendiente de la recta
Ecuación punto-pendiente de la recta que pasa por el punto 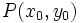 y tiene pendiente
y tiene pendiente 
|
|
Partimos de la ecuación explícita
Sustituimos el punto 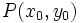 en la ecuación y despejamos
en la ecuación y despejamos  :
:
Sustituimos este valor de  en la ecuación explícita y sacamos factor común
en la ecuación explícita y sacamos factor común  :
:
Ejemplo: Ecuación punto-pendiente de la recta
Halla la ecuación punto-pendiente de la recta que pasa por los puntos A(5,-1) y B(7,4).
Primero calculamos su pendiente:
Usando el punto A(5,-1), la ecuación punto-pendiente queda así:
Ecuación punto-pendiente de la recta
Ejercicios sobre la ecuación punto-pendiente de la recta
Halla la ecuación punto-pendiente de la recta que pasa por los puntos A(3,4) y B(5,8).
En esta escena podrás ver como se obtiene la ecuación punto-pendientede la recta.
|
Actividad: Ecuaciones de la recta Representa la recta de ecuación 2x+5y-4=0. Exprésala en su forma punto-pendiente y explícita. Halla los puntos de corte con los ejes y su pendiente. Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión:
|
Rectas especiales
Rectas horizontales y verticales
Ejercicios y videotutoriales
Primer tutorial dedicado a las ecuaciones (analíticas) de la recta. En este tutorial se explica la ecuación vectorial, paramétrica y continua, con ejemplos y propiedades.
- 00:00 a 03:15: Símil entre dibujar una recta en una hoja y su expresión matemática en forma analítica (ecuación vectorial).
- 03:15 a 07:00: Ecuación Vectorial de una recta + Ejemplo.
- 07:00 a 08:50: Uso de la herramienta de DESMOS (https://www.desmos.com/calculator) para la explicación visual de la ecuación vectorial.
- 08:50 a 11:25: Ecuación Paramétrica de una recta + Ejemplo.
- 11:25 a 14:40: Ecuación Continua de una recta + Ejemplo.
- 14:40 a 15:55: Resumen de las ecuaciones de la recta trabajadas.
- 15:55 a 18:20: Ejemplo final de repaso.
Segundo tutorial dedicado a las ecuaciones (analíticas) de la recta. En este tutorial se explica la ecuación general/implícita y explícita, con ejemplos y propiedades.
- 00:00 a 01:25: Repaso del vídeo anterior: Ecuación vectorial, paramétrica y continua.
- 01:25 a 06:20: Ecuación General o Implícita y vector ortogonal a la recta + Ejemplo.
- 06:20 a 11:20: Ecuación Explícita y la pendiente de la recta + Ejemplo.
- 11:20 a 12:55: Ejemplo adicional en el uso de la propiedad de la pendiente de la recta.
- 12:55 a 13:20: Resumen de las ecuaciones de la recta trabajadas.
- 13:20 a 15:39: Ejemplo final de repaso.
Tercer tutorial dedicado a las ecuaciones (analíticas) de la recta. En este tutorial se explica la ecuación simétrica/canónica y punto pendiente, con ejemplos y propiedades.
- 00:00 a 01:30: Repaso de los vídeos anteriores: Ecuación vectorial, paramétrica, continua, general/implícita y explícita.
- 01:30 a 06:05: Ecuación Simétrica/Canónica de la recta + Ejemplo. Propiedad de los puntos de corte con los ejes.
- 06:05 a 08:50: Ecuación Punto Pendiente de la recta + Ejemplo.
- 08:50 a 11:36: Propiedad de la pendiente m = dY/dX.
- 11:36 a 12:20: Resumen de las ecuaciones de la recta trabajadas.
- 12:20 a 15:00: Ejemplo final de repaso.
Una recta del plano puede identificarse de las diversas formas que explicamos en este vídeo: ecuación vectorial, ecuaciones paramétricas, ecuación continua, ecuación punto-pendiente, ecuación explícita.
Radiografía de la recta que pasa por un punto dado con vector director dado. Resuelto con todo lujo de detalles, de modo que al profesor se le caigan los pantalones al ver tu forma de trabajar.
Ecuaciones de la recta en sus distintas formas dadas sus ecuaciones paramétricas.
Ecuaciones de la recta en sus distintas formas dadas sus ecuaciones paramétricas.
Ecuaciones de la recta en sus distintas formas dada su ecuación continua.
Ecuaciones de la recta en sus distintas formas dada su ecuación explícita.
Ecuaciones de la recta que pasa por dos puntos dados.
Representa gráficamente rectas dadas en distintas formas.
Hallar el baricentro de un triángulo conocidos sus 3 vértices.
Halla las ecuaciones de los lados de un triángulo conocidas las coordenadas de los vértices.
- Halla la mediana que pasan por el vértice A de un triángulo conocidas las coordenadas de los vértices.
- Halla las alturas que pasan por los vértices A y B.
- Halla la mediatriz del lado AB.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones de la recta en el plano |
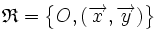
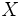 de la recta queda determinado de la siguiente manera:
de la recta queda determinado de la siguiente manera:
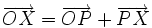
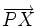

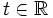 es un parámetro que, al variar, va generando los distintos puntos de la recta.
es un parámetro que, al variar, va generando los distintos puntos de la recta.