Estrategia de la altura para resolver triángulos oblicuángulos (1ºBach)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 114)
Estrategia de la altura
La estrategia de la altuta es un método para resolver triángulos oblicuángulos que consiste en elegir convenientemente una de las alturas del triángulo, de manera que ésta lo divida en dos triángulos rectángulos que puedan resolverse con los datos que nos den.
Cálculo de la altura y del área de un triángulo oblicuángulo
Altura y área de un triángulo
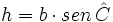
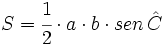 |
- Altura: Consideremos un triángulo oblicuángulo ABC como el de la figura adjunta. Si conocemos el ángulo
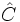 y el lado
y el lado  ), podemos obtener el valor de la altura utilizando el seno del ángulo dado.
), podemos obtener el valor de la altura utilizando el seno del ángulo dado.
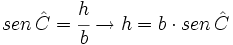
- Área: Consideremos un triángulo oblicuángulo ABC anterior. Teniendo en cuenta el valor de la altura que hemos obtenido en la demostración anterior, tenemos:
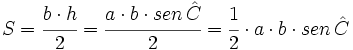
Cálculo de las proyecciones de los lados de un triángulo sobre la base
Proyecciones sobre la base
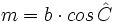 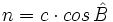 |
Consideremos un triángulo oblicuángulo ABC como el de la figura adjunta. Si conocemos el ángulo 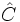 y el lado
y el lado  ), podemos obtener el valor de la proyección
), podemos obtener el valor de la proyección  sobre la base, utilizando el coseno del ángulo
sobre la base, utilizando el coseno del ángulo 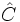 :
:
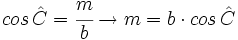
Analogamente para la proyección  :
:
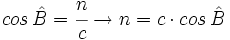
Ejercicio resuelto: Cálculo de las proyecciones, de la altura y del área
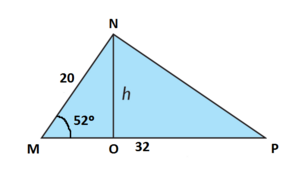
En un triángulo MNP:
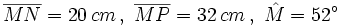
a) Halla la proyección de MN sobre MP.
b) Halla su área.
Estrategia de la altura para resolver triángulos oblicuángulos.
"Estamos en A. Conocemos las distancias de A a C (b=3800 m) y de C a B (a=5600 m). Queremos calcular la distancia de A a B."
Método de doble observación
El método de doble observación se utiliza cuando tenemos que hallar una altura de un objeto y tenemos como datos dos ángulos de observación desde dos puntos que están separados una distancia también conocida. También el dato conocido puede ser la altura y lo que tenemos que hallar es la distancia entre los puntos de observación.
Método de doble observación
El problema puede variar en cuanto a los datos y a las incógnitas, pero mantiene como técnica el aplicar la tangente a los dos ángulos observados para plantear un sistema similar al anterior.
Ejemplo: Método de doble observación
| Con objeto de determinar la altura de un árbol situado en un lugar inaccesible, se dispone un teodolito en un punto accesible y desde el mismo se lanza una visual al punto más alto del árbol, obteniéndose un ángulo de inclinación de 22º 47'.
A continuación, se adelanta el teodolito una distancia de 10 m en dirección al árbol y se vuelve a lanzar otra visual al mismo punto, obteniéndose, en este caso, un ángulo de 31º 19'. Calcula la altura del árbol, considerando que el anteojo del teodolito está a 1.5 m del suelo. |
Sea 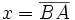 . La altura del árbol será
. La altura del árbol será 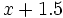 , pués hay que tener en cuenta la altura del teodolito.
, pués hay que tener en cuenta la altura del teodolito.
En el triángulo BAD:
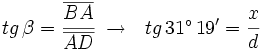
Por otra parte, en el triángulo BAC:
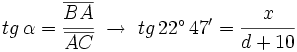
obtenemos el siguiente sistema de ecuaciones:
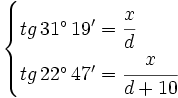
equivalente a:
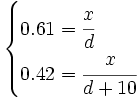
Que podemos resolver por el método de igualación despejando x en ambas ecuaciones:
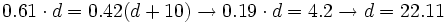
Y despejando x de una de la primera ecuación del sistema:
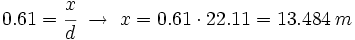
Por tanto, la altura del árbol es:
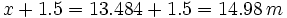
Problemas de doble observación.
Determina la altura de un árbol sabiendo que cuando el sol levanta 30º sobre el horizonte proyecta una sombra 12 m más larga que cuando el sol levanta 60º.
Una persona de 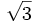 m de altura observa la parte superior de un poste con un ángulo de elevación de
m de altura observa la parte superior de un poste con un ángulo de elevación de 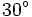 . Se acerca 8 m y vuelve a observar el anterior punto con un ángulo de elevación de
. Se acerca 8 m y vuelve a observar el anterior punto con un ángulo de elevación de 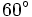 . Halla la altura del poste
. Halla la altura del poste
Desde la parte superior de un edificio de 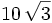 m de altura, se observa un auto que se aleja con un ángulo de depresión de
m de altura, se observa un auto que se aleja con un ángulo de depresión de 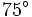 y después de 15 segundos con un ángulo de depresión de
y después de 15 segundos con un ángulo de depresión de 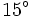 . Halla la velocidad del auto en m/s.
. Halla la velocidad del auto en m/s.
El piloto de un avión divisa una pequeña isla con un ángulo de depresión de 30º. Transcurridos 30 segundos el aviador nota que ese ángulo pasa a ser de 45º. Determina a qué altura vuela el avión sabiendo que su velocidad es de 400 m/s.
Problema que usa el método de doble observación.
Problema que usa el método de doble observación.
Problemas que usan el método de doble observación.
El ángulo de elevación del extremo de un mástil es de 53º, y caminando hacia él, crece hasta 64º. Halla la altura del mástil.
Desde dos puntos de una playa separados 300 m se ve un barco bajo ángulos de 30º y 65º, respectivamente. Calcula la distancia del barco a la playa
Desde un cierto punto del suelo se ve el punto más alto de una torre formando un ángulo de 30º con la horizontal. Si nos acercamos 75 m hacia el pie de la torre, este ángulo mide 60º. Calcula la altura de la torre.
Para medir la altura de una torre, dos observadores se estiran en el suelo, cada uno a un lado de la torre, a 50 m el uno del otro, y miden el ángulo que forma su visual con el extremo superior de la torre, 80º y 70º, respectivamente. Calcula la altura de la torre.
Para calcular cuanto mide un rio de ancho, medimos , desde dos puntos A y B de la orilla donde estamos, el ángulo que forma el curso del rio con la visual a un punto, C, de la otra orilla, y obtenemos 40º y 50º, respectivamente. Medimos también la distancia entre A y B, 45 m. Calcula la anchura del rio.
Estamos en P, situado en un llano. Queremos hallar la altura de una montaña, M. Para ello medimos el ángulo P que forma la visual a la montaña con la horizontal (P=29º). Avanzamos 300 m hacia la montaña y volvemos a medir el ángulo (Q=32º).
Halla la altura de una torre rodeada por un foso (base inaccesible) usando el método de doble observación.
Problemas resueltos sobre cómo calcular alturas o distancias usando el método de doble observación conocidos los ángulos de elevación desde 2 puntos distintos.
Problemas resueltos sobre cómo calcular alturas o distancias usando el método de doble observación conocidos los ángulos de depresión desde un mismo punto.
Teoremas del cateto y de la altura
Tutorial en el que se demuestra tanto el teorema de la altura como del cateto y aplica dichos teorema a la representación en la recta numérica de raíces cuadradas.
- 00:00 a 10:00: Demostración del Teorema de la Altura y del Cateto mediante la semejanza de triángulos.
- 10:00 a 10:35: Enunciado del Teorema de la Altura.
- 10:40 a 11:10: Enunciado del Teorema del Cateto.
- 11:10 a 15:40: Aplicación del Teorema de Pitágoras para representar raíces cuadradas..
- 15:50 a 19:45: Aplicación del Teorema de la Altura para representar raíces cuadradas..
- 19:45 a 22:15: Aplicación del Teorema del Cateto para representar raíces cuadradas.
Teoremas de la altura y del cateto. Ejemplos.
Teorema del cateto En todo triángulo rectángulo, un cateto, 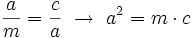 Y análogamente con el otro cateto, 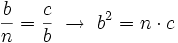 Demostración: Véase cualquiera de los siguientes videotutoriales.
Uno de los catetos de un triángulo rectángulo mide 16.5 cm y su proyección sobre la hipotenusa mide 7.5 cm. Halla el otro cateto, la proyección del otro cateto sobre la hipotenusa y la altura sobre la hipotenusa. En un triángulo rectángulo los catetos miden 20 y 21 cm. Calcula el valor de las proyecciones de los catetos sobre la hipotenusa. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla a medida de los catetos. En un triángulo rectángulo uno de los catetos mide 12 cm, y su proyección sobre la hipotenusa 9 cm. Calcula la hipotenusa y el otro cateto. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 25 y 36 m, respectivamente. Halla a medida de la hipotenusa. Teorema de la altura En todo triángulo rectángulo, la altura, 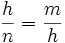 Demostración: Véase cualquiera de los siguientes videotutoriales:
Las proyecciones de los actetos sobre la hipotenusa de un triángulo rectángulo miden 18 m y 32 m, respectivamente. Halla la medida de los catetos y la de la altura sobre la hipotenusa. Problema de aplicación del teorema de la altura En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla la altura sobre la hipotenusa. Una torre eléctrica está sujeta al suelo con dos tensores. La distancia entre los pies de ambos tensores es 50 m. Los cables que sujetan la torre forman un ángulo recto y miden 30 y 40 m, respectivamente. Calcula la altura de la torre. En un triángulo rectángulo los catetos miden 20 y 21 cm, respectivamente. Calcula la altura del triángulo que cae sobre la hipotenusa. |
Actividades
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
- El ángulo opuesto al lado desigual de un triángulo isósceles es de 50º, y la altura correspondiente a dicho lado mide 8 cm. Determina el área del triángulo.
- Area del triángulo isósceles cuyo lado desigual mide 8 cm y su ángulo opuesto 40º.
- El lado desigual de un triángulo isósceles mide 8 cm, siendo de 25º sus ángulos adyacentes. Determina el área del triángulo.
- Los lados iguales de un triángulo isósceles miden 8 cm y forman 50º. Halla su área.
halla el área de un hexágono regular de 8 cm de lado.
halla el área de un octógono regular de 6 cm de lado.
Halla el área de un pentágono regular inscrito en una circunferencia de 8 cm de lado.
Un triángulo tiene un ángulo de 45º y otro de 65º. además el lado opuesto al de 45º mide 12 cm. Halla los otros dos lados.
Halla el área de un segmento circular de 12 cm de radio y amplitud 27º.
Problema de móviles.
Los ángulos de elevación del punto más alto un poste de 5 m, son de 60º y 40º. Averigua la distancia entre los puntos de observación y las distancias desde dichos puntos al punto más alto del poste.
2 problemas sobre la estrategia de la altura para resolver triángulos oblicuángulos.
2 problemas sobre la estrategia de la altura para resolver triángulos oblicuángulos.
Ejercicios propuestos
|
Ejercicios propuestos: Estrategia de la altura para resolver triángulos oblicuángulos |
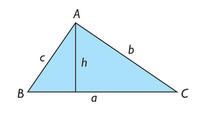
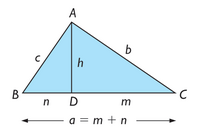
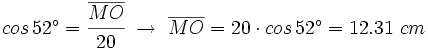
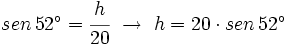
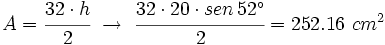
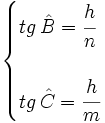

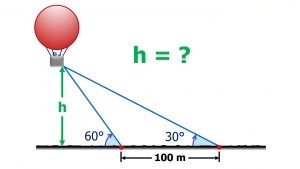
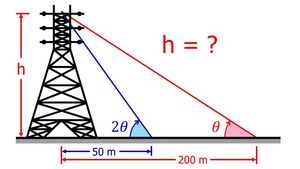
 , es media proporcional entre la hipotenusa,
, es media proporcional entre la hipotenusa, 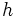 , y la proyección,
, y la proyección,  , de dicho cateto sobre la hipotenusa,
, de dicho cateto sobre la hipotenusa,  .
.
 , y su proyección,
, y su proyección,  .
.


