Plantilla:Estudio del crecimiento y de los puntos singulares
De Wikipedia
Procedimiento
Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:
- En aquellos puntos donde la derivada sea positiva la función será creciente.
- En aquellos puntos donde la derivada sea negativa la función será decreciente.
Funciones crecientes y decrecientes
Criterios de crecimiento y decrecimiento
Estudia el crecimiento de 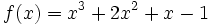
Estudia el crecimiento de 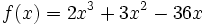
Estudia el crecimiento de 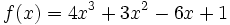
Estudia el crecimiento de 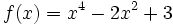
Estudia el crecimiento de 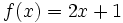
Estudia el crecimiento de 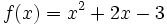
Estudia el crecimiento de 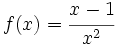
Demuestra que 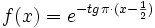 es positiva y decreciente en el intervalo (0,1).
es positiva y decreciente en el intervalo (0,1).
Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.
Esos puntos pueden ser puntos extremos (máximos o mínimos), pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.
Monotonía y extremos relativos
Monotonía y extremos relativos.Ejemplos
¿Qué son los puntos máximos, mínimos, locales y globales, crecimiento y decrecimiento?
Determinación de los extremos relativos
Determinación de máximos y mínimos absolutos
Estudia el crecimiento de 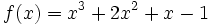
Estudia el crecimiento de 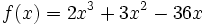
Estudia el crecimiento de 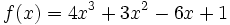
Estudia el crecimiento de 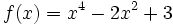
Halla los máximos y mínimos de 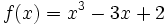
Encuentra el valor de "k" tal que 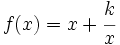 tenga un máximo local en x=-2.
tenga un máximo local en x=-2.
Halla los máximos y mínimos de 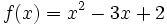
Halla los máximos y mínimos de 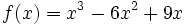
Halla los máximos y mínimos de 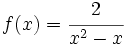
Halla los máximos y mínimos de 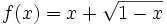
Halla los máximos y mínimos de 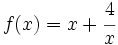
Ejercicio resuelto: Puntos singulares y crecimiento
Dada la función 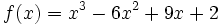 , halla sus puntos singulares y estudia su crecimiento.
, halla sus puntos singulares y estudia su crecimiento.
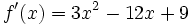
Puntos singulares:
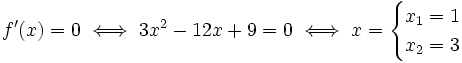
Para estudiar el crecimiento determinaremos el signo de la función derivada mediante una tabla en la que estableceremos zonas delimitadas por los puntos singulares y por los puntos de discontinuidad, si los hubiese. En nuestro caso hay 3 zonas porque hay 2 puntos singulares y no hay discontinuidades, por tratarse f'(x) de una función polinómica.
-inf 1 3 +inf
-----!------!-------!------!
f'(x)! + ! - ! + !
-----!------!-------!------!
f(x)! Cre ! Decre ! Cre !
----------------------------
Como f(1)=6 y f(3)=2, el anterior análisis del crecimiento nos permite determinar que (1,6) es un máximo y (3,2) es un mínimo.
