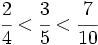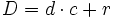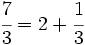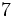Números Racionales. Fracciones (4ºESO-A)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Fracciones y números racionales
Los números enteros son útiles para contar u ordenar objetos, pero hay veces en las que es necesario dividir la unidad en partes iguales para poder expresar una medida: la mitad, la tercera parte, etc. Estas medidas se expresan por medio de fracciones.- Una fracción se expresa de la forma
 con
con 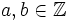 , donde
, donde  se llama numerador y
se llama numerador y  denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos. El valor de una fracción es el resultado de dividir numerador entre denominador.
denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos. El valor de una fracción es el resultado de dividir numerador entre denominador.
- Al conjunto de todas las fracciones también se le llama conjunto de números racionales. Lo representaremos por
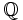 .
.
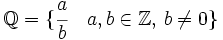
Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales.
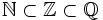 |
Representación de fracciones en la recta numérica
|
Actividades Interactivas: Representación de fracciones en la recta numérica
Actividad 1: Aprende a representar fracciones en la recta numérica.
Actividad 2: Autoevaluación: Averigua la posición de cada fracción en la recta numérica.
Actividad 3: Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica: a)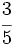 b) b) 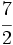 c) c)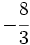 d) d) 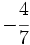 e) e) 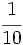 f) f) 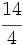 Actividad:
|
Fracciones propias e impropias
Fracciones propias son aquellas cuyo numerador es menor que el denominador. Son menores que 1.
Fracciones impropias son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1.
Proposición: Transformar una fración impropia en un entero más una fracción propia
- Toda fracción impropia
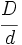 se puede escribir en la forma
se puede escribir en la forma 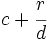 donde
donde  es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
Ejemplo: Fracciones impropias
- Descompón la frácción impropia
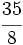 en la suma de un entero y una fracción propia.
en la suma de un entero y una fracción propia.
Dividimos 35 entre 8: 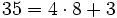
El dividendo 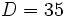 , el divisor
, el divisor 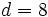 , el cociente
, el cociente 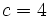 y el resto
y el resto 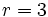 .
.
Aplicando la proposición anterior:
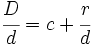
y sustituyendo cada letra por su valor:
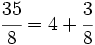
|
Calculadora: Fracciones impropias |
Fracciones equivalentes
Fracciones equivalentes son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.
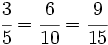
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
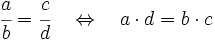
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debemos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción obtenida se dice que es irreducible.
Orden en el conjunto de los racionales
De dos fracciones con el mismo denominador, es mayor la de mayor numerador. Por eso, para ordenar fracciones, debemos primero obtener fracciones equivalentes a las dadas, pero con el mismo denominador. A ésto se le llama reducir a común denominador. Veamos un ejemplo:
Ejemplo: Ordenar fracciones
- Ordena las fracciones:
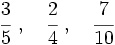
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
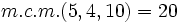 .
.Obtenemos fracciones equivalentes a las dadas con denominador 20. Para ello dividimos 20 entre cada denominador y lo multiplicamos por el numerador. Las fracciones obtenidas son:
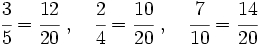
Estas fracciones las podemos ordenar fácilmente porque tienen el mismo denominador:
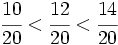
Así obtenemos: