Máximo común divisor (1º ESO)

De Wikipedia

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Máximo común divisor
2 Cálculo del máximo común divisor
- 2.1 Algoritmo de Euclides
3 Números primos entre sí
4 Problemas
5 Ejercicios propuestos

(Pág. 55)

[editar]

Máximo común divisor

El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.

Propiedades

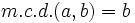Si $a\;$ es múltiplo de $b\;$ , entonces $m.c.d.(a,b)=b\;$ .
Los divisores comunes de varios números coinciden con los divisores del m.c.d.
Dados varios números, si se multiplican o dividen por otro número, entonces su m.c.d también queda multiplicado o dividido por el mismo número.
Dados dos números naturales, $a\;$ y $b\;$ , se cumple:

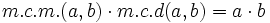
$m.c.m.(a,b) \cdot m.c.d (a,b)=a \cdot b$

Ejemplos

Un ejemplo de la primera propiedad:

m.c.d.(15, 30) = 15, porque 30 es múltiplo de 15.

Un ejemplo de la última propiedad:

m.c.d.(6,20) = 2 y m.c.m.(6,20) = 60

m.c.m.(6,20) · m.c.d.(6,20) = 2 · 60 = 120

a · b = 6 · 20 = 120.

[editar]

Cálculo del máximo común divisor

Ya sabemos encontrar todos los divisores de un número. Ahora nos interesa hallar un divisor en concreto. Queremos, de entre todos los divisores comunes a varios enteros, el mayor de ellos.

Y, ¿por qué el mayor?, ¿por qué un divisor común a varios números?, ¿para qué sirve esto?. Lo cierto es que el cálculo del máximo común divisor será muy útil para resolver problemas de divisibilidad en los que intervengan varios números. De ahí lo de común y lo de divisor. ¿Y por qué el mayor y no, por ejemplo, el menor? Piensa detenidamente... ¿Qué número es divisor de cualquier entero?. Efectivamente, el 1. ¿Crees que hay divisores menores que 1?

Una primera solución para encontrar el máximo común divisor de varios números podría ser calcular los divisores de cada uno de ellos y comprobar cuál es el mayor de los divisores comunes. A este método lo llamaremos "método artesanal".

Procedimiento artesanal

Para calcular el máximo común divisor de dos o más números se siguen los siguientes pasos:

Averiguaremos todos los divisores de dichos números.
De los divisores comunes (los que se repitan en todos) cogeremos el mayor.

Ejemplo:

Calcula el m.c.d.(24,60) por el método artesanal

Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24

Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

m.c.d.(24,60)= 12

Máximo común divisor (método artesanal)

Tutorial (6´36") Sinopsis:

Problemas prácticos en los que calcularemos el m.c.d. por el método artesanal.

Ejercicio 1 (5´56") Sinopsis:

Calcula:

a) m.c.d. (12, 8)

b) m.c.d. (25, 20)

c) m.c.d. (5, 12)

d) m.c.d. (6, 12)

Ejercicio 2 (4´48") Sinopsis:

Calcula el m.c.d. (-12, -30) hallando los divisores comunes.

Ejercicio 3 (6´13") Sinopsis:

Calcula hallando los divisores comunes:

a) m.c.d. (6, -12)

b) m.c.d. (-12, -15)

c) m.c.d. (-6, 8)

d) m.c.d. (0, -18)

e) m.c.d. (6, 4)

f) m.c.d. (8, -72)

Ejercicio 4 (6´15") Sinopsis:

Calcula hallando los divisores comunes:

a) m.c.d.(4, 16, 14)

b) m.c.d.(9, 12, 18)

c) m.c.d.(8, 16, 28)

d) m.c.d.(21, 27, 30)

Máximo común divisor (método artesanal)

Actividad 1 Descripción:

Actividad en la que podrás obtener el m.c.d. de dos números por el método artesanal.

Actividad 2 Descripción:

Actividad en la que podrás ver como se obtiene el m.c.d de dos números mediante el procedimiento artesanal.

Pero el método artesanal no es adecuado para números grandes pues requeriría muchos cálculos. Hay otro método basado en la factorización que es mucho más rápido. Lo llamaremos "método óptimo".

Sabemos que los divisores de un número son una combinación de algunos de sus factores primos. Por tanto, si queremos un divisor común a varios números, tendremos que tomar factores primos comunes a todos ellos. Si además queremos que sea el mayor de todos los divisores comunes, tendremos que tomar todos los factores que sean comunes.

Procedimiento óptimo

Para obtener el m.c.d. de dos o más números se siguen los siguientes pasos:

Se descomponen los números en factores primos.
Se toman los factores comunes con menor exponente.
Se multiplican dichos factores y el resultado obtenido es el m.c.d.

Observación:

En el caso de que no haya ningún factor común, en realidad nos estamos olvidando del 1, que aunque no es primo, es factor de cualquier número entero. Por tanto, si no hay coincidencia de ningún factor primo, el máximo común divisor es 1.

Ejemplo:

Calcula el m.c.d.(24,60) por el método óptimo

Descomponemos 24 y 60 en sus factores primos:

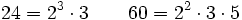
$24=2^3 \cdot 3 \qquad 60=2^2 \cdot 3 \cdot 5$

Multiplicando los factores comunes elevados al menor exponente:

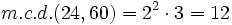
$m.c.d.(24,60)= 2^2 \cdot 3=12$

Calcula el m.c.d.(17,19) por el método óptimo

Descomponemos 17 y 19 en sus factores primos (incluimos al 1 aunque no sea primo):

$17=17 \cdot 1 \qquad 19=19 \cdot 1$

El único factor común es 1:

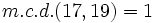
$m.c.d.(17,19)= 1\;$

Máximo común divisor

Tutorial 1 (13´46") Sinopsis:

Tutorial que explica el significado del máximo común divisor, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los divisores de los números, para el caso de número pequeños, o el algoritmo general.

00:00 a 07:33: ¿Qué es el máximo común divisor? Método de extracción de divisores.
07:33 a 13:46: Método general para calcular el m.c.d. Ejemplos.

Tutorial 2 (9´57") Sinopsis:

Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos o tres números.

Tutorial 3 (14´36") Sinopsis:

Concepto y cálculo del máximo común divisor de dos o más números.

Tutorial 4 (3´34") Sinopsis:

Concepto de máximo común divisor. Ejemplo.

Tutorial 5 (2´04") Sinopsis:

Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos números. Desarrolla un ejemplo en el que calcula el m.c.d. mediante el método artesanal.

Ejercicio 1 (1'01") Sinopsis:

Cálcula el máximo común divisor de 12 y 20

Ejercicio 2 (6'19") Sinopsis:

Cálcula el máximo común divisor de:

a) 12 y 18

b) 360 y 84

c) 40, 72 y 300

Ejercicio 3 (5'52") Sinopsis:

Cálcula el máximo común divisor de:

a) 30 y 45

b) 36, 84 y 120

Ejercicio 4 (14'59") Sinopsis:

Cálcula el máximo común divisor de:

a) 18 y 24

b) 36, 54 y 90

Ejercicio 5 (6'22") Sinopsis:

Calcula:

a) m.c.d.(36, 48).

b) m.c.d.(60, 90, 150).

Ejercicio 6 (9´06") Sinopsis:

Calcula:

a) m.c.d.(15, 20)

b) m.c.d.(12, 18)

c) m.c.d.(16, 20, 24)

d) m.c.d.(18, 27)

Ejercicio 7 (8´10") Sinopsis:

Calcula:

a) m.c.d.(8, 20)

b) m.c.d.(96, 160, 24)

Ejercicio 8 (6'17") Sinopsis:

Calcula: m.c.d.(48, 36, 84).

Ejercicio 9 (4'46") Sinopsis:

Calcula: m.c.d.(72, 108, 60).

Ejercicio 10 (2´09") Sinopsis:

3) Escribe los divisores de 4 y los divisores de 8.

a) ¿Es 4 divisor de 8?

b) ¿Son todos los divisores de 4 también divisores de 8?

c) ¿Es 8 divisor de 4?

d) ¿Son todos los divisores de 8 también divisores de 4?

e) ¿Cuál es el m.c.d. de 4 y 8?

Ejercicio 11 (10´37") Sinopsis:

Calcula:

a) m.c.d (16, 8)

b) m.c.d (40, 45)

c) m.c.d (9, 6)

d) m.c.d.(105, 30)

Máximo común divisor

Actividad 1 Descripción:

Actividad en la que podrás obtener el m.c.d. de dos números por descomposición factorial.
Actividad en la que deberás obtener el m.c.d. de dos números por descomposición factorial.

Actividad 2 Descripción:

Actividades sobre el máximo común divisor.

Actividad 3 Descripción:

Juego para practicar el m.c.d.

Autoevaluación 1 Descripción:

Ejercicios de autoevaluación sobre el m.c.d.

Autoevaluación 2 Descripción:

Ejercicios de autoevaluación sobre el m.c.d.

Autoevaluación 3 (Nivel avanzado) Descripción:

Ejercicios de autoevaluación sobre el m.c.d. (Nivel avanzado)

Máximo común divisor

Actividad: Máximo común divisor

a) Halla el m.c.d.(30,150,700)

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) gcd(30, 150, 700)

[editar]

Algoritmo de Euclides

Proposición

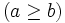Sean $a\;$ y $b\;$ , $(a \ge b)\;$ , dos números naturales, entonces se cumple que:

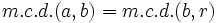
$m.c.d.(a,b)=m.c.d.(b,r)\;$

donde $r\;$ es el resto de la división de $a\;$ entre $b\;$ .

Apoyándonos en el resultado anterior tenemos el siguiente algoritmo para el cáculo del m.c.d. de dos números.

Algoritmo de Euclides

El algoritmo de Euclides es un procedimiento para calcular el m.c.d. de dos números. Los pasos son:

Se divide el número mayor entre el menor.

Si la división es exacta, el divisor es el m.c.d.
Si la división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m.c.d.

El algoritmo de Euclides

Tutorial 1 (5'43") Sinopsis:

Cálculo del m.c.d. usando el algoritmo de Euclides.

Tutorial 2 (4'45") Sinopsis:

Euclides.
Ejemlplos de cálculo del m.c.d. usando el algoritmo de Euclides.

Tutorial 3 (3'31") Sinopsis:

Cálculo del m.c.d. y del m.c.m. usando el algoritmo de Euclides.

Ejercicio 1 (6'00") Sinopsis:

Calcula el m.c.d. de 364 y 748 usando el algoritmo de Euclides.

Ejercicio 2 (4'15") Sinopsis:

Calcula el m.c.d. de 136 y 48 usando el algoritmo de Euclides.

Ejercicio 3 (5'55") Sinopsis:

Calcula el m.c.d. de 44 y 24 usando el método artesanal y el algoritmo de Euclides.

Ejercicio 4 (5'52") Sinopsis:

Calcula el m.c.d. de 100 y 150 usando el método artesanal y el algoritmo de Euclides.

Autoevaluación: Algoritmo de Euclides Descripción:

Ejercicios de autoevaluación sobre el algoritmo de Euclides.

[editar]

Números primos entre sí

Dos o más números son primos entre sí o coprimos, si su m.c.d. es 1, es decir, no tienen divisores comunes salvo la unidad.

Ejemplo

6 y 11 son primos entre sí ya que no tienen divisores comunes salvo el 1.
6 y 27 no son primos entre sí porque tienen como divisor común a 3.

Números primos entre sí

Tutorial (0´44") Sinopsis:

¿Cuándo son dos números primos entre sí?. Ejemplo.

Ejercicio 1 (0´46") Sinopsis:

Comprueba si los números 3 y 7 son o no primos entre sí.

Ejercicio 2 (0´51") Sinopsis:

Comprueba si los números 11 y 22 son o no primos entre sí.

Ejercicio 3 (1´09") Sinopsis:

Comprueba si los números 9 y 48 son o no primos entre sí.

Ejercicio 4 (1´02") Sinopsis:

Comprueba si los números 45 y 34 son o no primos entre sí.

Ejercicio 5 (1´21") Sinopsis:

Comprueba si los números 6, 8 y 20 son o no primos entre sí.

Propiedades

Si a y b son primos entre sí, entonces m.c.m.(a,b)=a · b.
Si se dividen varios números por su m.c.d., los cocientes resultantes son primos entre sí.

Ejemplo

Como 6 y 11 son primos entre sí, entonces m.c.m(6,11)=6·11=66
Sean los números 1 y 25. Su m.c.d.(10,25)=5

10:5=2 y 25:5=5; m.c.d.(2,5)=1, luego 2 y 5 son primos entre sí.

[editar]

Problemas

Problema resuelto: m.c.d.

En un almacén quieren envasar, para su distribución, 200 kg de manzanas y 260 kg de de naranjas, en cajones del mismo peso y de la mayor carga que sea posible. ¿Cuántos kilos deben poner en cada cajón?

Solución:

Solucuión: 20 kg

Problemas: Máximo común divisor

Problema 1 (6´03") Sinopsis:

Iker ha cocinado 24 galletas de chocolate, 16 de manzana y 20 buñuelos. Quiere colocarlo todo en platos que contengan un solo tipo de postre y con el mismo número de unidades. Si quiere utilizar el menos número de platos posible, ¿cómo debe hacerlo?.

Problema 2 (5´40") Sinopsis:

Se desea dividir un terreno rectangular cuyas dimensiones son de 186 m y 162 m, en parcelas cuadradas, para lo cual se colocan estacas en cada uno de los vértices de las parcelas. ¿Cuántas estacas se necesitarán colocar en total como mínimo?

Problema 3 (6´30") Sinopsis:

En una bodega hay 3 toneles de vino, cuyas capacidades son 250, 360 y 540 litros. Se quiere envasar todo el vino en botellas iguales lo más grandes posible. Calcula la capacidad de estas botellas y cuántas serán necesarias.

Problema 4 (2´20") Sinopsis:

Un comerciante tiene dos barriles llenos de vino: uno de vino tinto, cuya capacidad es de 250 litros, y otro de vino moscatel, de 160 litros. Para efectos de comercialización y transporte requiere distribuir todo el vino de ambos barriles, sin mezclar los contenidos, en recipientes de igual capacidad, de modo que el número de estos sea el menor posible y estén completamente llenos. ¿Qué cantidad de estos recipientes necesitará para el vino moscatel?

Problema 5 (4´33") Sinopsis:

Tres cables que miden 20, 150 y 180 metros se dividen en el menor número de trozos de igual longitud. ¿Cuál es la longitud de cada trozo?

A) 5 m; B) 20 m; C) 12 m; D) 15 m; E) 10 m

Problema 6 (6´38") Sinopsis:

Un albañil debe colocar losetas cuadradas en un piso de un baño cuyas dimensiones son 270 cm y 300 cm. ¿Cuántas losetas enteras entrarán en dicho piso, si estas deben ser del mayor tamaño posible?

A) 30; B) 90; C) 10; D) 19

Problema 7 (8´29") Sinopsis:

Las edades de dos amigos son como 4 es a 7. Si el mínimo común múltiplo de sus edades es 168 y su máximo común divisor es 6, ¿Cuáles son sus edades?

A) 24 y 48; B) 24 y 36; C) 12 y 24; D) 24 y 42

Problema 8 (3´50") Sinopsis:

Camila tiene 24 bocadillos y 20 zumos para repartir en bolsas. Cada bolsa tiene que tener el mismo número de bocadillos y el mismo número de zumos. ¿Cuántas bolsas, como máximo, necesita? ¿Cuántos zumos y cuántos bocadillos mete en cada bolsa?

Nivel más avanzado:

Problema 1 (7´47") Sinopsis:

Si tienes que llenar 4 cilindros de capacidades 72, 24, 56 y 120 galones respectivamente. ¿Cuál es la capacidad del balde que puede usarse para llenarlos exactamente si está comprendida entre 2 y 8 galones?

Problema 2 (8´23") Sinopsis:

Juan tiene un terreno de forma rectangular de 40m de ancho y 96m de largo. si se divide su terreno en parcelas cuadradas iguales y planta en el interior de cada parcela 3 árboles, ¿cuál es el mínimo número de árboles que podría sembrar en todo su terreno?

a) 160; b) 150; c) 190; d) 170; e) 180

Problema 3 (8´09") Sinopsis:

Raúl compró cierto número de televisores por S/.31500 y vendió unos cuantos en S/15000, cobrando cada televisor lo mismo que le había costado. ¿Cuántos televisores le quedan si el precio de estos es el mayor posible?

a) 11; b) 9; c) 13; d) 10; e) 12

Problema 4 (10´29") Sinopsis:

Se desea colocar postes igualmente espaciados en el perímetro de un terreno rectangular de 280 m de largo por 120 m de ancho. Si se sabe que debe colocarse un poste en cada esquina y el número de postes debe ser el menor posible, determínese el número total de postes por colocar.

A) 24; B) 20; C) 48; D) 40; E) 18

Problemas: Máximo común divisor

Problema 1 Descripción:

Un comerciante desea poner en cajas 6690 manzanas y 6630 naranjas, de modo que cada caja contenga el mismo número de piezas de fruta, y además, el mayor número posible. Halla el número de piezas de fruta de cada caja.

Problema 2 Descripción:

¿Cuántos centímetros mide el lado de la mayor baldosa que cabe un número exacto de veces en una sala de 20 m de largo y 16 m de ancho?

[editar]