Radicales: Operaciones (4ºESO-A)
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Potencias y Raíces | WIRIS Calculadora Raíz cuadrada |
Radical
Se llama radical a cualquier expresión en la que aparezcan raíces
Operaciones con radicales del mismo índice
Para multiplicar radicales del mismo índice se deja el índice y se multiplican los radicandos
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Cociente:
Para dividir radicales del mismo índice, se deja el índice y se dividen los radicandos.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Potencia:
Para elevar un radical a una potencia se eleva el radicando a dicha potencia, manteniendo el índice.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Radical:
Para hallar el radical de un radical se multiplican los índices de ambos.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Radicales
Actividad 1. Operaciones con radicales del mismo índice.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Suma y resta de radicales con el mismo índice y radicando
Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice.
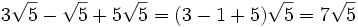
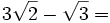 (No se puede simplificar)
(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png) (No se puede simplificar)
(No se puede simplificar)
Racionalización de fracciones
Racionalizar una fracción consiste en encontrar una fracción equivalente que no tenga radicales en el denominador.
Extracción e introducción de factores en un radical (ampliación)
Extracción de factores
Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introducción de factores
Para introducir factores dentro de un radical se multiplica el exponente del factor por el índice del radical.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Introducción y extracción de factores de un radical
Actividad 1. Introduce y extráe factores de radicales.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Suma y resta de radicales con el mismo índice y distinto radicando (ampliación)
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando:
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Suma y resta de radicales
Actividad 1. Suma y resta radicales con el mismo índice y distinto radicando.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Producto y cocientes de radicales de distinto índice (ampliación)
Para multiplicar o dividir radicales con distintos índices, éstos deben tener el mismo radicando. En tal caso, los radicales los convertimos en potencias de la misma base y operamos con ellas, para obtener una única potencia, que posemos volver a poner en forma radical.
![3\sqrt[3]{5} \cdot \sqrt[4]{5}:\sqrt{5}=3\cdot5^{\frac{1}{3}}\cdot5^{\frac{1}{4}}:5^{\frac{1}{2}}=3\cdot5^{(\frac{1}{3}+\frac{1}{4}-\frac{1}{2})}=3\cdot5^\frac{1}{12}=3\sqrt[12]{5}](/wikipedia/images/math/b/1/a/b1a9fbc1341d8f63d5659188b2def312.png)
![3\sqrt[5]{2}-\sqrt[3]{3}=](/wikipedia/images/math/2/d/6/2d6ed3298d1c8572ad52fb6df78ce017.png) (No se puede simplificar)
(No se puede simplificar)
(Otro método: sin pasar a potencia de exponente fraccionario. Ver también: Radicales equivalentes)

