Semejanza de Triángulos Rectángulos (4ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Semejanza entre triángulos rectángulos
Cuando los triángulos son rectángulos, las condiciones para que sean semejantes se reducen.
Proposición
Dos triángulos rectángulos son semejantes si se cumple una de las siguientes condiciones:
- Tienen un ángulo agudo igual.
- Tienen dos lados proporcionales.
La sombra que proyecta una madre de 1.70 m de altura, a las 2 de la tarde, es de 2 m. ¿Qué altura tiene el hijo si la sombra que proyecta es de 1.8 m?.
Un palo de 2 m colocado verticalmente proyecta una sombra de 95 cm. Indica la altura de un edificio que a la misma hora proyecta una sombra de 20 m.
Dados los triángulos rectángulos del dibujo, halla su razón de semejanza sabiendo que tienen un ángulo agudo igual.
Teoremas del cateto y de la altura
Tutorial en el que se demuestra tanto el teorema de la altura como del cateto y aplica dichos teorema a la representación en la recta numérica de raíces cuadradas.
- 00:00 a 10:00: Demostración del Teorema de la Altura y del Cateto mediante la semejanza de triángulos.
- 10:00 a 10:35: Enunciado del Teorema de la Altura.
- 10:40 a 11:10: Enunciado del Teorema del Cateto.
- 11:10 a 15:40: Aplicación del Teorema de Pitágoras para representar raíces cuadradas..
- 15:50 a 19:45: Aplicación del Teorema de la Altura para representar raíces cuadradas..
- 19:45 a 22:15: Aplicación del Teorema del Cateto para representar raíces cuadradas.
Teoremas de la altura y del cateto. Ejemplos.
Teorema del cateto En todo triángulo rectángulo, un cateto, 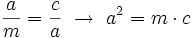 Y análogamente con el otro cateto, 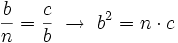 Demostración: Véase cualquiera de los siguientes videotutoriales.
Uno de los catetos de un triángulo rectángulo mide 16.5 cm y su proyección sobre la hipotenusa mide 7.5 cm. Halla el otro cateto, la proyección del otro cateto sobre la hipotenusa y la altura sobre la hipotenusa. En un triángulo rectángulo los catetos miden 20 y 21 cm. Calcula el valor de las proyecciones de los catetos sobre la hipotenusa. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla a medida de los catetos. En un triángulo rectángulo uno de los catetos mide 12 cm, y su proyección sobre la hipotenusa 9 cm. Calcula la hipotenusa y el otro cateto. En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 25 y 36 m, respectivamente. Halla a medida de la hipotenusa. Teorema de la altura En todo triángulo rectángulo, la altura, 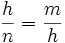 Demostración: Véase cualquiera de los siguientes videotutoriales:
Las proyecciones de los actetos sobre la hipotenusa de un triángulo rectángulo miden 18 m y 32 m, respectivamente. Halla la medida de los catetos y la de la altura sobre la hipotenusa. Problema de aplicación del teorema de la altura En un triángulo rectángulo las proyecciones de los catetos sobre la hipotenusa miden 2 y 10 cm, respectivamente. Halla la altura sobre la hipotenusa. Una torre eléctrica está sujeta al suelo con dos tensores. La distancia entre los pies de ambos tensores es 50 m. Los cables que sujetan la torre forman un ángulo recto y miden 30 y 40 m, respectivamente. Calcula la altura de la torre. En un triángulo rectángulo los catetos miden 20 y 21 cm, respectivamente. Calcula la altura del triángulo que cae sobre la hipotenusa. |
Ejercicios propuestos
|
Ejercicios propuestos: Semejanza de triángulos rectángulos |
 , es media proporcional entre la hipotenusa,
, es media proporcional entre la hipotenusa, 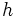 , y la proyección,
, y la proyección,  , de dicho cateto sobre la hipotenusa,
, de dicho cateto sobre la hipotenusa,  .
.
 , y su proyección,
, y su proyección,  .
.


