Ampliación del concepto de ángulo (1ºBach)
De Wikipedia
| Revisión de 09:01 18 feb 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:02 18 feb 2019 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| ==Ejercicios== | ==Ejercicios== | ||
| - | {{AI_upr | + | {{Actividades: Ampliación del concepto de ángulo}} |
| - | |titulo1=Razones trigonométricas de ángulos "especiales" | + | |
| - | |descripcion=Da el valor exacto de la razón trigonométrica de un ángulo "especial". | + | |
| - | |url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=Precalculo2_soluciones/trig_funang/funangle.db&no_ques=8 | ||
| - | }} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 09:02 18 feb 2019
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
(Pág. 108)
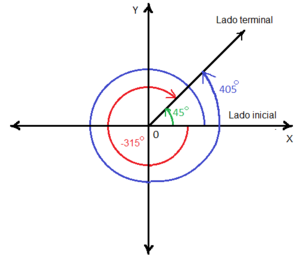
Hasta ahora hemos trabajado con ángulos comprendidos entre 0º y 360º. Vamos a extender el estudio a ángulos con una medida mayor que 360º. Igualmente haremos con ángulos negativos.
Ángulos coterminales
Dos ángulos, Propiedades Los ángulos coterminales se diferencian en un número entero de vueltas a la circunferencia goniométrica. Es decir, 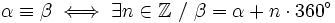 . . |
Propiedades
- Los ángulos coterminales tienen las mismas razones trigonométricas.
- Dado un ángulo mayor que 360º, existe un ángulo comprendido entre 0º y 360º coterminal con él, que es el resto de la división entre el ángulo y 360º.
- Dado un ángulo negativo, existe un ángulo positivo coterminal con él.
- Los ángulos coterminales tienen las mismas razones trigonométricas, por tener la misma posición en la circunferencia goniométrica.
- Dado un ángulo mayor que 360º, existe un ángulo comprendido entre 0º y 360º coterminal con él, que es el resto de la división entre el ángulo y 360º, ya que, al hacer la división y quedarnos con el resto, le estamos quitando un número exacto de vueltas y por tanto obteniendo uno coterminal con él.
- Dado un ángulo negativo, existe un ángulo positivo coterminal con él pués basta con sumarle 360º un número suficiente de veces.
- El ángulo -60º tiene por coterminal al ángulo 300º (-60º+360º). Por tanto, las razones trigonométricas de -60º y 300º son las mismas.
Si un ángulo  tiene medida superior a 360º, al ángulo
tiene medida superior a 360º, al ángulo 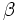 con medida inferior a 360º coterminal con
con medida inferior a 360º coterminal con  , decimos que es la reducción al primer giro de
, decimos que es la reducción al primer giro de  .
.
- 3000º es coterminal con 120º porque la división 3000:360 da 120 de resto. Entonces 120º es la recucción al primer giro de 3000º.
Definición de ángulos coterminales. Ejemplos.
- Si un ángulo orientado "A" tiene medida superior a 360º, del único ángulo "B" con medida inferior a 360º coterminal con "A", decimos que es la reducción al primer giro de "A".
- Ejemplos.
|
Actividad: Ampliación del concepto de ángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
Da el valor exacto de la razón trigonométrica de un ángulo "especial".
Ejercicios propuestos
|
Ejercicios propuestos: Angulos coterminales |
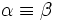 ) si tienen el mismo vértice, el mismo lado inicial y el mismo lado final.
) si tienen el mismo vértice, el mismo lado inicial y el mismo lado final.