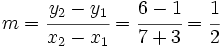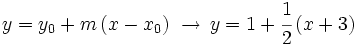Ecuaciones de una recta en el plano (1ºBach)
De Wikipedia
| Revisión de 10:21 12 oct 2016 Coordinador (Discusión | contribuciones) (→Ecuación explícita de la recta) ← Ir a diferencia anterior |
Revisión de 10:22 12 oct 2016 Coordinador (Discusión | contribuciones) (→Ecuación explícita de la recta) Ir a siguiente diferencia → |
||
| Línea 277: | Línea 277: | ||
| Pero en una proposición anterior vimos que el vector <math>(-B,A)\,</math> era el vector de dirección de la recta. | Pero en una proposición anterior vimos que el vector <math>(-B,A)\,</math> era el vector de dirección de la recta. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Pendiente de una recta''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la siguiente escena puedes comprobar la segunda de las proposiciones anteriores sobre la pendiente de la recta que pasa por dos puntos. | ||
| - | |actividad=Toma nota de las coordenadas de los puntos <math>P_1\,</math> y <math>P_2\,</math> y calcula la pendiente con la fórmula: <math>m=\cfrac{y_2-y_1}{x_2-x_1}</math> | ||
| - | Comprueba los resultados en la siguiente escena: | ||
| - | |||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_6_3.html | ||
| - | width=490 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_6_3.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | |||
| - | Prueba a cambiar los valores en la escena para obtener otros puntos. Por ejemplo, con los puntos <math>P_1(-2,5)\,</math> y <math>P_2(1,-1)\,</math>, calcula la pendiente y comprueba los resultados. | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| {{p}} | {{p}} | ||
Revisión de 10:22 12 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Vector de dirección de una recta
- Una recta
 queda determinada por un punto
queda determinada por un punto  y un vector
y un vector 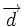 que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
- Dos puntos
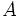 y
y 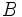 de una recta determinan un vector de dirección de la misma,
de una recta determinan un vector de dirección de la misma, 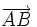 .
.
En esta escena podrás ver como un punto del plano y un vector director determinan una recta.
En esta escena podrás ver como dos puntos del plano determinan una recta.
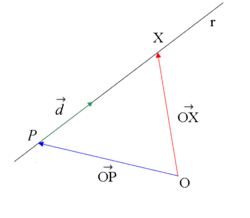
Ecuación vectorial de la recta
En esta escena podrás ver como se representa la ecuación vectorial de una recta en el plano.
Ecuaciones paramétricas de la recta
Ecuaciones paramétricas de la recta con vector de dirección 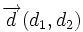 y que pasa por el punto
y que pasa por el punto 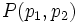 .
.
|
|
A partir de la ecuación verctorial de la recta
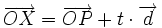
si sustituimos cada vector por sus coordenadas, tenemos:
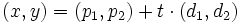
En esta escena podrás ver como se representan las ecuaciones paramétricas de una recta en el plano.
Ecuación continua de la recta
Ecuación continua de la recta con vector director 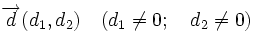 y que pasa por un punto
y que pasa por un punto 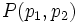 :
:
|
|
A partir de las ecuaciones paramétricas de la recta, despejando el parámetro 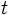 (siempre y cuando las dos coordenadas del vector
(siempre y cuando las dos coordenadas del vector 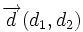 sean distintas de cero), tenemos:
sean distintas de cero), tenemos:
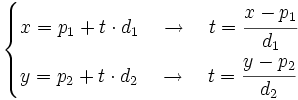
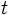 , obtenemos la ecuación.
, obtenemos la ecuación.Ejemplo: Ecuación continua de la recta
Halla la ecuación continua de la recta con vector director 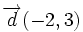 que pasa por el punto
que pasa por el punto 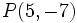 .
.
De las ecuaciones paramétricas despejamos el parámetro 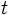 e igualamos:
e igualamos:
Ecuación implícita de la recta
Ecuación implícita de la recta:
|
|
Partiendo de la ecuación continua de la recta: (suponemos que 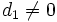 y
y 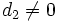 )
)
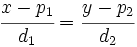
Multiplicando en cruz:
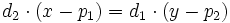
y pasando todos los términos a la izquierda de la ecuación, tenemos:
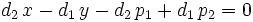
de donde, haciendo: 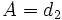 ,
, 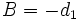 y
y 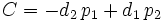
se tiene la ecuación.
Antes hemos supuesto 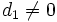 y
y 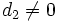 . Si, por el contrario, alguno fuera cero tendríamos:
. Si, por el contrario, alguno fuera cero tendríamos:
- Si
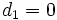 , las ecuaciones paramétricas serían:
, las ecuaciones paramétricas serían:
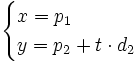
de donde se tiene que la recta es vertical con ecuación 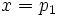 y su ecuación implícita sería
y su ecuación implícita sería 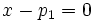 .
.
- Si
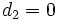 , las ecuaciones paramétricas serían:
, las ecuaciones paramétricas serían:
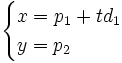
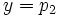 y su ecuación implícita sería
y su ecuación implícita sería 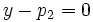 .
.Ejemplo: Ecuación implícita de la recta
Halla la ecuación implícita de la recta que pasa por los puntos 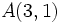 y
y 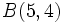 .
.
Primero calculamos su vector de dirección:
Obtenemos las ecuaciones paramétricas con ese vector director y con uno de los dos puntos, por ejemplo 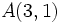 . A partir de éstas obtenemos la ecuación continua:
. A partir de éstas obtenemos la ecuación continua:
Multiplicando en cruz y pasando todos los términos a la izquierda de la ecuación, obtenemos la ecuación implícita:
Proposición
Dada una recta de ecuación 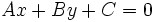 :
:
- El vector
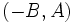 es un vector de dirección de la recta.
es un vector de dirección de la recta.
- El vector
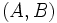 es un vector perpendicular a la recta que se denomina vector normal a la recta.
es un vector perpendicular a la recta que se denomina vector normal a la recta.
Antes vimos, en la deducción de la ecuación explícita, que partiendo de la ecuación continua y haciendo 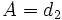 ,
, 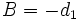 y
y 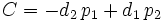 , se tenía la ecuación implícita
, se tenía la ecuación implícita 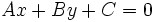 .
.
Entonces, el vector 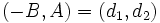 , que es el vector director de la recta
, que es el vector director de la recta
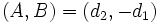 es perpendicular a la recta porque
es perpendicular a la recta porque 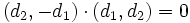 , y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.
, y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.Ecuación explícita de la recta
Ecuación explícita de la recta:
|
|
donde  se llama pendiente de la recta y
se llama pendiente de la recta y  ordenada en el origen.
ordenada en el origen.
Partiendo de la ecuación implícita
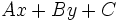
y despejando 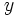 (siempre que
(siempre que 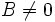 ), tenemos:
), tenemos:
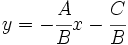
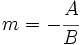 y
y 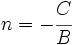 , tenemos la ecuación.
, tenemos la ecuación.Estudio del comportamiento de la recta y=mx+n atendiendo a los parámetros m (pendiente) y n (ordenada en el origen).
Ejemplo: Ecuación explícita de la recta
- Halla la ecuación explícita de la recta de ecuaciones paramétricas:
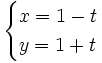
Partimos de las ecuaciones paramétricas y obtenemos su ecuación continua.
Para obtener la ecuación explícita basta con despejar 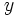 :
:
En esta escena podrás ver las distintas ecuaciones de la recta.
Proposición
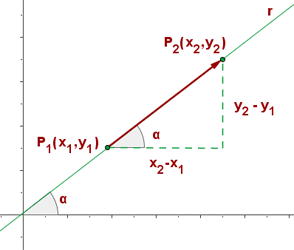
- La pendiente de una recta mide el incremento de la ordenada cuando la abcisa se incrementa en una unidad.
- Si
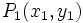 y
y 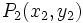 son dos puntos de la recta, entonces su pendiente es
son dos puntos de la recta, entonces su pendiente es 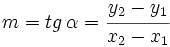
- El vector de coordenadas
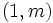 es un vector de dirección de la recta.
es un vector de dirección de la recta.
1. Sean 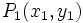 y
y 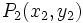 , dos puntos de la rectan y tomemos
, dos puntos de la rectan y tomemos 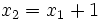 .
.
Sus abcisas 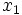 y
y 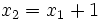 difieren en 1.
difieren en 1.
Veamos sus ordenadas en cuanto difieren:
2. Por la definición de tangente de un ángulo:
3. En la deducción de la ecuación explícita vimos que 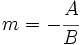 , entonces:
, entonces:
Si multiplicamos ambas coordenadas por 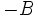 , obtenemos otro vector con la misma dirección:
, obtenemos otro vector con la misma dirección:
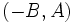 era el vector de dirección de la recta.
era el vector de dirección de la recta.Ecuación de la recta que pasa por dos puntos
Sabemos que dos puntos determinan un vector de dirección. Con ese vector de dirección y uno de los dos puntos podemos obtener la ecuación de la recta.
En esta escena podrás ver como se obtiene la ecuación de la recta que pasa por dos puntos.
Ecuación punto-pendiente de la recta
Ecuación punto-pendiente de la recta que pasa por el punto 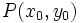 y tiene pendiente
y tiene pendiente 
|
|
Partimos de la ecuación explícita
Sustituimos el punto 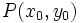 en la ecuación y despejamos
en la ecuación y despejamos  :
:
Sustituimos este valor de  en la ecuación explícita y sacamos factor común
en la ecuación explícita y sacamos factor común  :
:
|
Actividad interactiva: Ecuación punto-pendiente de la recta Actividad 1: En la siguiente escena vamos a hallar la ecuación punto-pendiente de la recta que pasa por los puntos Actividad: Primero calculamos la pendiente: Con esta pendiente y uno de los puntos, por ejemplo, Comprueba los resultados en la siguiente escena:
|
Videotutoriales
Una recta del plano puede identificarse de las diversas formas que explicamos en este vídeo: ecuación vectorial, ecuaciones paramétricas, ecuación continua, ecuación punto-pendiente, ecuación explícita.
Ecuaciones de la recta en sus distintas formas dado un punto y un vector director.
Ecuaciones de la recta en sus distintas formas dadas sus ecuaciones paramétricas.
Ecuaciones de la recta en sus distintas formas dadas sus ecuaciones paramétricas.
Ecuaciones de la recta en sus distintas formas dada su ecuación continua.
Ecuaciones de la recta en sus distintas formas dada su ecuación explícita.
Ecuaciones de la recta que pasa por dos puntos dados.
Dibujar rectas dadas en distintas formas.
Hallar el baricentro de un triángulo conocidos sus 3 vértices.
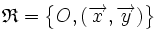
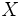 de la recta queda determinado de la siguiente manera:
de la recta queda determinado de la siguiente manera:
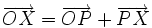
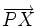

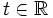 es un parámetro que, al variar, va generando los distintos puntos de la recta.
es un parámetro que, al variar, va generando los distintos puntos de la recta.
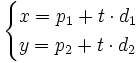
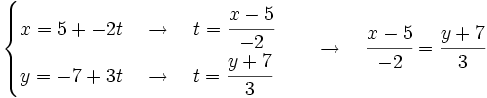
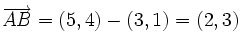
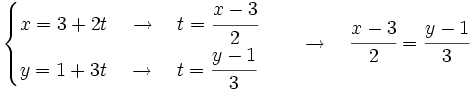
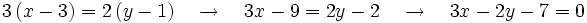
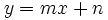
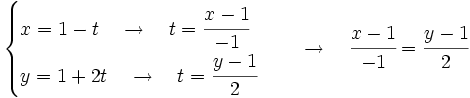
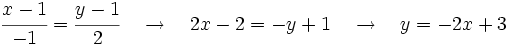
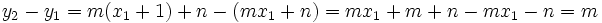
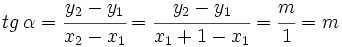
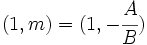
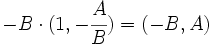
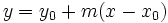
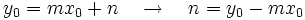
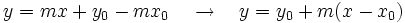
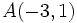 y
y 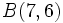 .
.