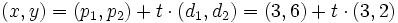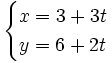Ecuaciones de una recta en el plano (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Vector de dirección de una recta
- Una recta
 queda determinada por un punto
queda determinada por un punto  y un vector
y un vector 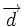 que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
que fije su dirección. A dicho vector lo llamaremos vector de dirección de la recta.
- Dos puntos
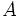 y
y 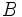 de una recta determinan un vector de dirección de la misma,
de una recta determinan un vector de dirección de la misma, 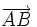 .
.
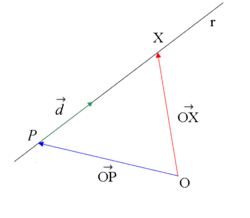
Ecuación vectorial de la recta
|
Actividad interactiva: Ecuación vectorial de la recta Actividad 1: En la siguiente escena veremos como se obtienen los distintos puntos de una recta utilizando su ecuación vectorial. Actividad: Modifica el parámetro 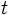 y observa como se obtienen distintos puntos de la recta. y observa como se obtienen distintos puntos de la recta.
|
Ecuaciones paramétricas de la recta
A partir de la ecuación verctorial de la recta
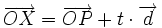
si sustituimos cada vector por sus coordenadas, tenemos:
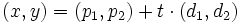
Igualando coordenada a coordenada, obtenemos las siguientes ecuaciones:
Ecuaciones paramétricas de la recta  , con vector de dirección
, con vector de dirección 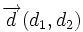 y que pasa por el punto
y que pasa por el punto 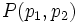 .
.
|
|
|
Actividad interactiva: Ecuaciones paramétricas de la recta Actividad 1: En la siguiente escena tenemos la recta con vector de dirección Actividad: Su ecuación vectorial es: y sus ecuaciones paramétricas: Modifica el parámetro
|
Ecuación continua de la recta
A partir de las ecuaciones paramétricas de la recta, despejando el parámetro 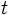 (siempre y cuando las dos coordenadas del vector
(siempre y cuando las dos coordenadas del vector 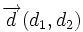 sean distintas de cero), tenemos:
sean distintas de cero), tenemos:
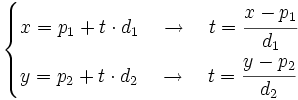
Igualando ambos valores de 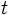 , obtenemos la siguiente ecuación:
, obtenemos la siguiente ecuación:
Ecuación continua de la recta  , con vector director
, con vector director 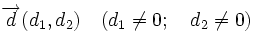 y que pasa por un punto
y que pasa por un punto 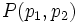 :
:
|
|
Ecuación implícita de la recta
Partiendo de la ecuación continua de la recta: (suponemos que 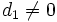 y
y 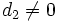 )
)
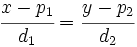
Multiplicando en cruz:
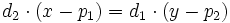
y pasando todos los términos a la izquierda de la ecuación, tenemos:
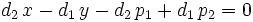
de donde, haciendo 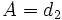 ,
, 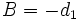 y
y 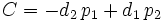 , se tiene la siguiente ecuación:
, se tiene la siguiente ecuación:
Ecuación implícita de la recta  :
:
|
|
Antes hemos supuesto 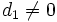 y
y 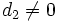 . Si, por el contrario, alguno fuera cero tendríamos:
. Si, por el contrario, alguno fuera cero tendríamos:
- Si
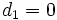 , de las ecuaciones paramétricas serían,
, de las ecuaciones paramétricas serían, 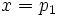 e
e 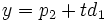 , de donde se tiene que la recta es vertical con ecuación
, de donde se tiene que la recta es vertical con ecuación 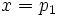 . Su ecuación implícita sería
. Su ecuación implícita sería 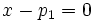 .
.
- Si
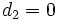 , de las ecuaciones paramétricas serían,
, de las ecuaciones paramétricas serían, 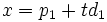 e
e 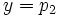 , de donde se tiene que la recta es horizontal con ecuación
, de donde se tiene que la recta es horizontal con ecuación 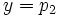 . Su ecuación implícita sería
. Su ecuación implícita sería 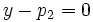 .
.
Proposición
Dada una recta de ecuación 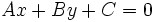 :
:
- El vector
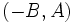 es un vector de dirección de la recta.
es un vector de dirección de la recta.
- El vector
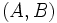 es un vector perpendicular a la recta.
es un vector perpendicular a la recta.
Antes vimos, en la deducción de la ecuación explícita, que partiendo de la ecuación continua y haciendo 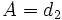 ,
, 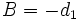 y
y 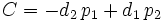 , se tenía la ecuación implícita
, se tenía la ecuación implícita 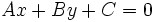 .
.
Entonces, el vector (-B, A)=(d_1,d_2), que es el vector director de la recta
Y el vector (A,B)=(d_2, -d_1) es perpendicular a la recta porque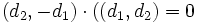 , y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.
, y sabemos que si el producto escalar de dos vectores vale cero, éstos son ortogonales.Ecuación explícita de la recta
Estudio "no vectorial" de la recta
- La función lineal.
- Representación gráfica de una recta a partir de su ecuación.
- Pendiente de una recta.
- Representación gráfica de una recta a partir de su pendiente y de un punto por el que pasa.
- Rectas perpendiculares al eje de abscisas.
- Deducción geométrica de la ecuación de la recta que pasa por dos puntos.
- Ejemplos.
- Deducción geométrica de la ecuación de la recta que pasa por un punto dado con pendiente dada.
- Ejemplos.
- Distintas formas de escribir la ecuación de la recta.
- Ejemplos.
- Rectas paralelas: relación entre sus pendientes. Ejemplos y problemas.
- Rectas perpendiculares: relación entre sus pendientes. Ejemplos y problemas.
- Cálculo de la tasa de variación de una recta.
- Ejemplos
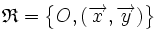
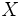 de la recta queda determinado de la siguiente manera:
de la recta queda determinado de la siguiente manera:
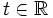 es un parámetro que, al variar, va generando los distintos puntos de la recta.
es un parámetro que, al variar, va generando los distintos puntos de la recta.
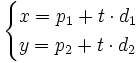
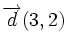
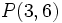 . Veremos como se obtienen los distintos puntos de una recta utilizando sus ecuaciones paramétricas.
. Veremos como se obtienen los distintos puntos de una recta utilizando sus ecuaciones paramétricas.