Estrategia de la altura para resolver triángulos oblicuángulos (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:35 22 feb 2009 Coordinador (Discusión | contribuciones) (→Cálculo de la altura de un triángulo oblicuángulo) ← Ir a diferencia anterior |
Revisión de 16:49 22 feb 2009 Coordinador (Discusión | contribuciones) (→Cálculo de la altura de un triángulo oblicuángulo) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Cálculo de la altura de un triángulo oblicuángulo== | + | ==Cálculo de la altura y del área de un triángulo oblicuángulo== |
| - | {{Teorema|titulo=Altura de un triángulo|enunciado= | + | {{Teorema|titulo=Altura y área de un triángulo|enunciado= |
| - | [[Imagen:altura_oblicuangulo.png|200px|right]] | + | {{Tabla75|celda2=<center>[[Imagen:altura_oblicuangulo.png|200px|]]</center> |
| - | La altura de un triángulo es igual al producto de uno de sus lados laterales (que no es la base) por el seno del ángulo que dicho lado forma con la base. | + | |celda1={{p}} |
| - | {{p}} | + | *La '''altura''' de un triángulo es igual al producto de uno de sus lados laterales (que no es la base) por el seno del ángulo que dicho lado forma con la base. |
| - | <center><math>h=c \cdot sen \, \hat B</math></center> | + | |
| {{p}} | {{p}} | ||
| <center><math>h=b \cdot sen \, \hat C</math></center> | <center><math>h=b \cdot sen \, \hat C</math></center> | ||
| - | <br> | + | |
| + | *El '''área''' de un triángulo es igual a la mitad del producto de dos de sus lados por el seno del ángulo que forman. | ||
| + | {{p}} | ||
| + | <center><math>S=\cfrac{1}{2} \cdot a \cdot b \cdot sen \, \hat C</math></center> | ||
| + | }} | ||
| |demo= | |demo= | ||
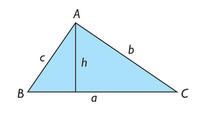
| - | Consideremos un triángulo oblicuángulo ABC como el de la figura adjunta. Si conocemos el ángulo <math>\hat B</math> y el lado <math>c\,</math> (o bien el ángulo <math>\hat C</math> y el lado <math>b\,</math>), podemos obtener el valor de la altura utilizando el seno del ángulo dado. | + | *'''Altura:''' Consideremos un triángulo oblicuángulo ABC como el de la figura adjunta. Si conocemos el ángulo <math>\hat C</math> y el lado <math>b\,</math>), podemos obtener el valor de la altura utilizando el seno del ángulo dado. |
| - | + | ||
| - | <center><math>sen \, \hat B=\cfrac{h}{c} \rightarrow h=c \cdot sen \, \hat B</math></center> | + | |
| <center><math>sen \, \hat C=\cfrac{h}{b} \rightarrow h=b \cdot sen \, \hat C</math></center> | <center><math>sen \, \hat C=\cfrac{h}{b} \rightarrow h=b \cdot sen \, \hat C</math></center> | ||
| + | |||
| + | *'''Área:''' Consideremos un triángulo oblicuángulo ABC anterior. Teniendo en cuenta el valor de la altura que hemos obtenido en la demostración anterior, tenemos: | ||
| + | |||
| + | <center><math>S=\cfrac{b \cdot h}{2}=\cfrac{a \cdot b \cdot sen \, \hat C}{2}=\cfrac{1}{2} \cdot a \cdot b \cdot sen \, \hat C</math></center> | ||
| + | |||
| + | <center><math>S=\cfrac{1}{2} \cdot a \cdot b \cdot sen \, \hat C</math></center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 16:49 22 feb 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Cálculo de la altura y del área de un triángulo oblicuángulo
Altura y área de un triángulo
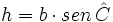
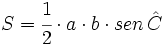 |
Demostración:
- Altura: Consideremos un triángulo oblicuángulo ABC como el de la figura adjunta. Si conocemos el ángulo
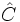 y el lado
y el lado  ), podemos obtener el valor de la altura utilizando el seno del ángulo dado.
), podemos obtener el valor de la altura utilizando el seno del ángulo dado.
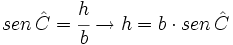
- Área: Consideremos un triángulo oblicuángulo ABC anterior. Teniendo en cuenta el valor de la altura que hemos obtenido en la demostración anterior, tenemos:
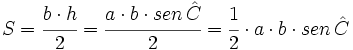
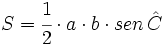
Estrategia de la altura
La estrategia de la altuta es un método para resolver triángulos oblicuángulos que consiste en elegir convenientemente una de las alturas del triángulo, de manera que ésta lo divida en dos triángulos rectángulos que puedan resolverse con los datos que nos den.
Ejercicios
|
Actividad interactiva: Estrategia de la altura
Actividad 1: Triángulos isósceles
Actividad:
Actividad 2: Otras aplicaciones.
Actividad:
|