Funciones: Introducción (1ºBach)
De Wikipedia
| Revisión de 08:06 30 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Introducción) |
||
| Línea 10: | Línea 10: | ||
| *El '''análisis matemático''' es una rama de las matemáticas que estudia los números reales, los complejos y las '''funciones''' entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de '''límite''' y estudia conceptos como la '''continuidad''', la '''integración''' y la '''derivación'''. | *El '''análisis matemático''' es una rama de las matemáticas que estudia los números reales, los complejos y las '''funciones''' entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de '''límite''' y estudia conceptos como la '''continuidad''', la '''integración''' y la '''derivación'''. | ||
| - | *El '''cálculo infinitesimal''' o simplemete '''Cálculo''' es una rama del análisis matemático que se divide en dos áreas: cálculo diferencial y cálculo integral. | + | *El '''[[Cálculo infinitesimal|cálculo infinitesimal]]''' o simplemete '''Cálculo''' es una rama del análisis matemático que se divide en dos áreas: cálculo diferencial y cálculo integral. |
| :*El '''[[Cálculo diferencial|cálculo diferencial]]''' es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la '''derivada'''. | :*El '''[[Cálculo diferencial|cálculo diferencial]]''' es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la '''derivada'''. | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Introducción
- El análisis matemático es una rama de las matemáticas que estudia los números reales, los complejos y las funciones entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de límite y estudia conceptos como la continuidad, la integración y la derivación.
- El cálculo infinitesimal o simplemete Cálculo es una rama del análisis matemático que se divide en dos áreas: cálculo diferencial y cálculo integral.
- El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada.
- El cálculo integral es una parte del análisis matemático que consiste en el estudio de las integrales. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.
Una de las diferencias entre el álgebra y el análisis es que en este segundo recurre a construcciones que involucran sucesiones de un número infinito de elementos, mientras que álgebra usualmente es finitista.
- Introducción al cálculo diferencial.
Sin duda Newton es el autor del primer paso de la carrera espacial. Las Leyes descubiertas por él son las que han permitido al hombre poner un pie en la Luna o enviar naves a Marte y Venus, explorar los planetas exteriores: Júpiter, Saturno, Neptuno y Urano. Su modelo de telescopio ha permitido ver más lejos en cielo. Sin duda los astrónomos le deben mucho a Newton. Pero los matemáticos, y de paso el resto de los científicos, le deben tanto o más. Él junto a Leibniz, aunque sería mejor decir al mismo tiempo que Leibniz, son los descubridores de la más potente y maravillosa herramienta matemática: el Cálculo. Newton tuvo en vida un prestigio y un reconocimiento social aún mayor que el que pudo tener Einstein en nuestro siglo. Como los reyes y muy pocos nobles fue enterrado en la abadía de Westminster. Leibniz murió sólo y abandonado por todos. A su entierro en Hannover sólo asistió su criado. Hoy los dos comparten por igual la gloria de ser los padres de las dos herramientas más potentes del universo matemático: el cálculo diferencial y el cálculo integral. El instrumento ideal para entender y explicar el funcionamiento del mundo real, desde las cosas más próximas hasta el rincón más alejado del universo.
Una breve historia de las funciones
En las matemáticas actuales el concepto de función se define del modo siguiente:
Sean A y B conjuntos. Se llama función entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B.
Para representar las funciones se suele utilizar la notación 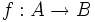 para los conjuntos,
para los conjuntos,  para los elementos. A se llama conjunto inicial y B es el conjunto final.
para los elementos. A se llama conjunto inicial y B es el conjunto final.
Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final)
de variable real (conjunto inicial), 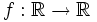 .
.
El concepto de función se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años.
Mesopotamia y antiguo Egipto
Comenzaremos en Mesopotamia. En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los
números naturales. Estas tablas sin duda definen funciones de 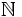 en
en 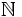 o de
o de 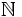 en
en  , lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.
, lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.
Grecia clásica
En la Grecia clásica también manejaron funciones particulares —incluso en un sentido moderno de relación entre los elementos de dos conjuntos y no sólo de fórmula— pero es poco probable que comprendieran el concepto abstracto moderno de función.
Edad Media
La mayor parte de los historiadores de las matemáticas parecen estar de acuerdo en atribuir a Nicole Oresme (1323-1382) la primera aproximación al concepto de función, cuando describió las leyes de la naturaleza como relaciones de dependencia entre dos magnitudes. Fue el primero en hacer uso sistemático de diagramas para representar magnitudes variables en un plano.Edad Moderna
En la revolución científica iniciada en el siglo XVI los científicos centraron su atención en los fenómenos de la naturaleza, poniendo énfasis en las relaciones entre las variables que determinaban dichos fenómenos y que podían ser expresadas en términos matemáticos. Era necesario comparar las variables, relacionarlas, expresarlas mediante números y representarlas en algún sistema geométrico adecuado.
Galileo Galilei (1564-1642) pareció entender el concepto de función aún con mayor claridad. Sus estudios sobre el movimiento contienen la clara comprensión de una relación entre variables.
Casi al mismo tiempo que Galileo llegaba a estas ideas, Renè Descartes (1596-1650) introducía la geometría analítica. Descartes desarrolló y llevó a sus fundamentales consecuencias las ideas que siglos atrás se habían usado para representar en el plano relaciones entre magnitudes. Ahora cualquier curva del plano podía ser expresada en términos de ecuaciones y cualquier ecuación que relacionara dos variables podía ser representada geométricamente en un plano.
Los matemáticos de la antigüedad, así como los matemáticos de la Edad Moderna hasta fines del siglo XVII, cuando debido a los trabajos de Newton y de Leibniz fue terminada la construcción del cálculo diferencial e integral, no tenían la definición general de la función. En aquel tiempo todavía no tenían necesidad de tal definición. Si a Newton o a Leibniz le preguntasen qué es “una función en general”, la respuesta, por lo visto, sería que “una función en general” es el resultado de ciertas operaciones (algebraicas o transcendentes elementales) con las variables independientes. Semejante definición apareció por primera vez en un trabajo del alumno y colaborador de Leibniz, Johan Bernoulli, en 1718. En este trabajo la función se definía como una “expresión analítica”: "una función es una cantidad formada de alguna manera a partir de cantidades indeterminadas y constantes".
El primer problema, en el que los matemáticos tuvieron la necesidad de tener una definición general de función, fue el problema de la cuerda vibrante. A este problema se dedicaban los más grandes matemáticos de los mediados del siglo XVIII D’Alembert y Euler.
En 1748, Euler entendía que una función es una curva, dibujada por un movimiento libre de la mano. Para D’Alembert, que era seguidor de la escuela de J. Bernoulli, una función era una expresión analítica. ¿Qué concepto es más amplio, cuál es más estrecho? La discusión entre D’Alembert y Euler duró varios años. En 1755, Euler, bajo la influencia de las argumentaciones de D’Alembert, dio pronto otra definición de función que es más “matemática” que la anterior en apariencia, pero no en esencia: Cuando unas cantidades dependen de otras de tal forma que al variar las últimas también varían las primeras, entonces las primeras se llaman funciones de las segundas. Esta nueva definición contiene tanto la definición de D’Alembert, como la anterior definición “mecánica” del mismo Euler.
Al mismo tiempo, puesto que en ella no se habla nada sobre la naturaleza permisible de la dependencia de las primeras cantidades de las segundas, la definición sigue siendo bastante difusa, así que cada uno de los posteriores matemáticos del siglo XVIII tenía libertad para interpretarla a su manera. En el gran curso de cálculo diferencial e integral, escrito por La Croix para la Escuela Politécnica de París (1797), está aceptada de hecho esta misma definición. Adicionalmente está introducida una indicación para decir que la naturaleza de la dependencia puede no ser conocida de antemano. S. La Croix, en 1797, da esta definición: Cualquier cantidad, cuyo valor depende de una o de otras varias cantidades, se llama función de estas últimas, independientemente de si se conocen o no las operaciones que hay que realizar para pasar de éstas a la primera.
Edad Contemporanea
Dirichlet, en 1837, da una definición satisfactoria del concepto de función: y es función de x, si a cada valor de x le corresponde un valor completamente determinado de la y; además no es importante el método con el que ha sido establecida la correspondencia señalada.
Lobachevski, en 1934: Una función de x es un número que se da a cada x y que varía constantemente con la x. El valor de la función puede estar dado o por una expresión analítica o por una condición que da el procedimiento para probar todos los números. La dependencia puede existir y quedarse desconocida.
Los matemáticos del siglo XIX suponían que los límites del desarrollo del análisis matemático habían sido establecidos por la definición de Dirichlet de una vez y para siempre. Pero a finales del siglo, los matemáticos constataron con sorpresa que la definición de Dirichlet, que parecía indiscutiblemente clara y precisa, contiene en sí inesperadas dificultades de principio, serias hasta tal punto, que muchos empezaron a negarse a admitir en ella algún sentido. Para aclarar esta cuestión, comparemos la definición de Lobachevski y la definición de Dirichlet aplicándolas al objeto siguiente. Supongamos que a cada número natural n=1,2,... le corresponde el número a(n) que es igual a 1, si en el desarrollo decimal del número pi hay n nueves seguidos; y es igual a cero en el caso contrario. ¿Se trata de una función de n o no? Dirichlet diría: “Está claro que esto es una función. Para cada n, o existen n nueves seguidos en el desarrollo del número pi, o no existen; la tercera posibilidad se excluye. Puesto que no impongo condiciones a la naturaleza de la dependencia, ante mí hay efectivamente una función definida con exactitud”. Lobachevski diría: “No conozco la regla que da para cada n la posibilidad de saber si en el desarrollo del número pi hay n nueves seguidos. Puede ser que esta regla no exista. Por consiguiente aquí no hay función”.
Los matemáticos se dividieron en dos tendencias: los partidarios de la definición de función “según Dirichlet”, que no exigían una regla obligatoria; y los partidarios de la definición de función “según Lobachevski”, que exigían una regla obligatoria, formada por un número finito de palabras. Los representantes de la segunda corriente, llamados intuicionistas, renunciaban a la mayor parte de análisis clásico y formaban la matemática intuicionista propia. Los representantes de la primera corriente, que no deseaban renunciar a los logros del análisis clásico, se resignaron a aceptar la existencia de muchos hechos paradójicos, que resultaban de la existencia de las funciones sin regla.
Actualmente se puede constatar que el posterior desarrollo de las matemáticas no había seguido el camino de los intuicionistas y al fin de cuentas los logros del análisis clásico se quedaron firmes.Sin embargo algunos resultados concretos de los intuicionistas encontraron en nuestros tiempos una aplicación inesperada en la teoría de las computadoras. El tratamiento informático solo pueden tener funciones que se definen mediante reglas con una cantidad finita de palabras y además esta cantidad tiene que ser relativamente pequeña.
Historia de las funciones (Parte 1)
Historia de las funciones (Parte 2)




