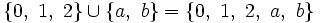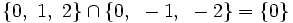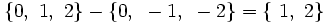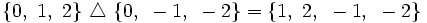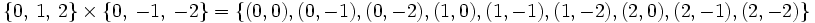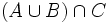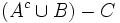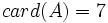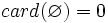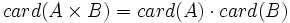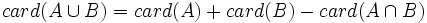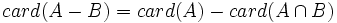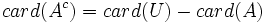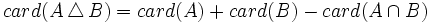Lenguaje matemático: conjuntos y símbolos (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 30)
Símbolos
Símbolos usados en definiciones y proposiciones
-
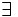 : Se lee "existe"
: Se lee "existe"
-
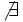 : Se lee "no existe"
: Se lee "no existe"
-
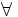 : Se lee "para todo"
: Se lee "para todo"
-
 : Se lee "tal que" (También se puede representar mediante dos puntos
: Se lee "tal que" (También se puede representar mediante dos puntos 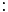 )
)
Igualdades y desigualdades
-
 : Se lee "es mayor que"
: Se lee "es mayor que"
-
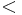 : Se lee "es menor que"
: Se lee "es menor que"
-
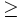 : Se lee "es mayor o igual que"
: Se lee "es mayor o igual que"
-
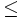 : Se lee "es menor o igual que"
: Se lee "es menor o igual que"
-
 : Se lee "es igual a"
: Se lee "es igual a"
-
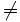 : Se lee "es distinto de"
: Se lee "es distinto de"
-
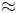 : Se lee "es aproximadamente igual a"
: Se lee "es aproximadamente igual a"
Conectores lógicos
- Negación:
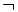 . Se lee "no".
. Se lee "no".
- Conjunción:
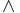 . Se lee "y".
. Se lee "y".
- Disyunción:
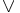 . Se lee "o".
. Se lee "o".
- Condicional:
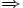 . Se lee "si...entonces".
. Se lee "si...entonces".
- Bicondicional:
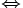 . Se lee "si y solo si" o "son equivalentes". (También suele escribirse "sii")
. Se lee "si y solo si" o "son equivalentes". (También suele escribirse "sii")
Sean las proposiciones P: "está lloviendo" y Q: "la calle está mojada", entonces:
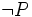 : "no está lloviendo".
: "no está lloviendo".
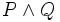 : "está lloviendo y la calle está mojada".
: "está lloviendo y la calle está mojada".
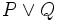 : "está lloviendo o la calle está mojada".
: "está lloviendo o la calle está mojada".
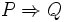 : "si está lloviendo entonces la calle está mojada".
: "si está lloviendo entonces la calle está mojada".
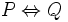 : "está lloviendo si y solo si la calle está mojada".
: "está lloviendo si y solo si la calle está mojada".
Conjuntos
-
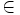 : Se lee "pertenece a"
: Se lee "pertenece a"
-
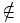 : Se lee "no pertenece a"
: Se lee "no pertenece a"
-
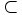 : Se lee "está incluido en"
: Se lee "está incluido en"
-
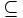 : Se lee "está incluido en o es igual a"
: Se lee "está incluido en o es igual a"
-
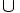 : Se lee "unión"
: Se lee "unión"
-
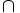 : Se lee "intersección"
: Se lee "intersección"
Conjuntos
El concepto de conjunto es primitivo, en el sentido de que no es posible definirlo en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere, pues, la introducción de axiomas y conduce a la teoría de conjuntos.
Si para los números naturales se considera la propiedad de "ser un número natural menor que 5", entonces, el conjunto de los números naturales que cumplen esa propiedad sería:
- Por extensión:
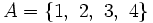
- Por comprensión:
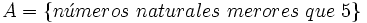 ó
ó 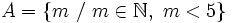
- (En la segunda expresión la barra oblicua "/" significa «tal que». En lugar de la barra oblicua se utiliza también la barra vertical " | " o los dos puntos ":")
Formas de determinar un conjunto: por comprensión y por extensión. Ejemplos.
Determinar por extensión un conjunto dado por comprensión
Determinar por comprensión un conjunto dado por extensión
Conjunto vacío
El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por 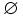 o
o 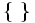 .
.
Conjunto universal
El conjunto universal, que denotaremos por 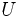 , es el conjunto que contiene todos los elementos posibles, dentro del contexto considerado.
, es el conjunto que contiene todos los elementos posibles, dentro del contexto considerado.
Relaciones entre conjuntos
Relación de pertenecia
Un elemento se dice que «pertenece» al conjunto y se denota mediante el símbolo Relación de igualdadUn conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa. Por ello, la relación de igualdad entre conjuntos se define como: Dos conjuntos A y B, son iguales (A=B) si y sólo si tienen los mismos elementos (Axioma de extensionalidad). |
Consecuencias del axioma de extensionalidad
Ejercicio sobre igualdad de conjuntos Relación de inclusión. Subconjuntos
| 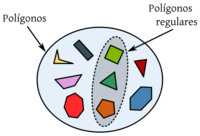 Fig.3 - Representación de la relación de inclusión mediante diagrama de Venn: Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos es otro conjunto, en particular, un subconjunto del primero. |
Ejercicio sobre la relación de pertenencia y de inclusión de conjuntos.
Dado un conjunto, 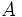 , se llama conjunto potencia de
, se llama conjunto potencia de 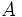 , y se denota por
, y se denota por 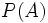 , al conjunto que tiene por elementos a todos los subconjuntos de
, al conjunto que tiene por elementos a todos los subconjuntos de 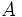 , .
, .
Definición de conjunto potencia. Ejemplos
Operaciones con conjuntos
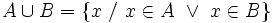
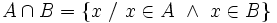
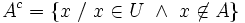
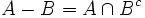
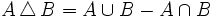
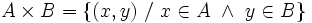 |
Operaciones con conjuntos: Unión, intersección, diferencia, diferencia simétrica y complementario. Ejemplos
Ejemplos sobre la unión de conjuntos.
Ejemplos sobre la intersección de conjuntos.
Ejemplo sobre el complementario de un conjunto.
Ejemplo sobre la diferencia de conjuntos.
Ejemplo sobre la diferencia simétrica de conjuntos.
Concepto de par ordenado. Ejemplos.
Ejemplos de producto cartesiano y de su representación gráfica
Ejercicio sobre operaciones con conjuntos.
Ejercicio sobre operaciones con conjuntos.
Ejercicio sobre operaciones con conjuntos.
Conjuntos disjuntos
Dos conjuntos A y B son disjuntos si no tienen ningún elemento en común. Es decir, su intersección es el conjunto vacio.
Diagrama de Carrol: Definición y ejemplos
Problema sobre diagramas de Carrol.
Problema sobre diagramas de Carrol.
Problema sobre diagramas de Carrol.
Problema sobre diagramas de Carrol.
Cardinal de un conjunto
- Los conjuntos pueden ser finitos o infinitos. En el caso de un conjunto finito se pueden contar los elementos del conjunto. El número de elementos de un conjunto finito es su cardinal. El cardinal se denota por
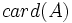 ,
, 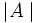 ó
ó 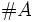 .
.
- En un conjunto infinito no hay un número finito de elementos. Es el caso, por ejemplo, de los números naturales. Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, de manera que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es un número transfinito.
- A los conjuntos con un solo elemento se les llama conjuntos unitarios.
Ejercicio sobre conjuntos unitarios.
Ejercicio sobre cardinales de conjuntos.
Ejercicio sobre cardinales de conjuntos.
Ejercicio sobre cardinales de conjuntos.
Ejercicio sobre cardinales de conjuntos.
Ejercicios propuestos
|
Ejercicios propuestos: Conjuntos y símbolos |
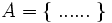 , siendo irrelevante el orden. Se puede hacer de dos maneras:
, siendo irrelevante el orden. Se puede hacer de dos maneras:

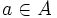 se lee «a pertenece a A». Para la noción contraria se usa el símbolo
se lee «a pertenece a A». Para la noción contraria se usa el símbolo 
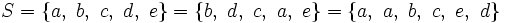
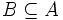 . También puede escribirse
. También puede escribirse 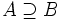 y se lee "B está incluido en A", "A contiene a B", "B está contenido en A", "A incluye a B" o "A es un superconjunto de B".
y se lee "B está incluido en A", "A contiene a B", "B está contenido en A", "A incluye a B" o "A es un superconjunto de B".
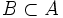 ó
ó 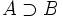
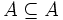
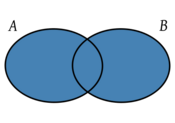
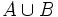 , es el conjunto de todos los elementos que pertenecen al menos a uno de los dos conjuntos.
, es el conjunto de todos los elementos que pertenecen al menos a uno de los dos conjuntos.
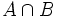 , es el conjunto de todos los elementos comunes a los dos conjuntos.
, es el conjunto de todos los elementos comunes a los dos conjuntos.
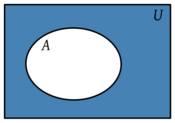
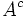 (o bien,
(o bien, 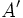 ) que contiene todos los elementos que no pertenecen a A, respecto a un conjunto universal U que lo contiene.
) que contiene todos los elementos que no pertenecen a A, respecto a un conjunto universal U que lo contiene.
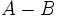 que resulta de eliminar de A cualquier elemento que esté en B.
que resulta de eliminar de A cualquier elemento que esté en B.
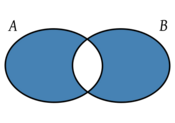
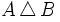 con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
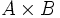 de todos los pares ordenados (a,b) formados con un primer elemento "a" perteneciente a A, y un segundo elemento "b" perteneciente a B.
de todos los pares ordenados (a,b) formados con un primer elemento "a" perteneciente a A, y un segundo elemento "b" perteneciente a B.