Plantilla:Esfera
De Wikipedia
| Revisión de 13:38 1 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:13 1 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| |descripcion=En esta escena podrás calcular el volumen y área de un balón de futbol. | |descripcion=En esta escena podrás calcular el volumen y área de un balón de futbol. | ||
| |enlace=[https://ggbm.at/DRMa7bXj Volúmen y área de la esfera] | |enlace=[https://ggbm.at/DRMa7bXj Volúmen y área de la esfera] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema|titulo=Teorema|enunciado=El volumen de la esfera es igual a dos tercios del volumen del cilindro circunscrito a ella. | ||
| + | |demo= | ||
| + | El cálculo del volumen de la esfera fue uno de los descubrimientos que Arquímedes más estimaba de todos los que hizo en su vida. Llegó a demostrar de un modo muy original que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella. Tanto le impresionó esto a él mismo que mandó que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas. | ||
| + | {{p}} | ||
| + | [[Imagen:esfera_cilindro.gif|center]] | ||
| + | {{p}} | ||
| + | Vamos a ver cómo llegó hasta ahí. Arquímedes se imaginó una semiesfera y junto a ella un cilindro circular recto y un cono recto, ambos de base igual a un círculo máximo de la semiesfera: | ||
| + | {{p}} | ||
| + | [[Imagen:esfera_cilindro_2.png|center]] | ||
| + | {{p}} | ||
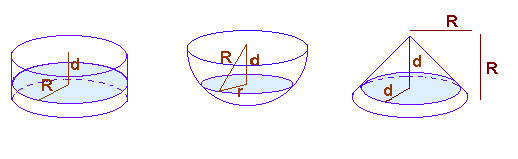
| + | Arquímedes cortó las tres figuras por un plano paralelo a la base del cilindro y cono y se preguntó cómo serían las secciones determinadas por este plano en cilindro, semiesfera y cono. | ||
| + | En el cilindro es un círculo de radio R. En la esfera también será un círculo, pero su radio dependerá de la distancia d. Mirando la figura y acordándote del teorema de Pitágoras, fácilmente puedes escribir que si el radio de la sección es r, entonces | ||
| + | {{p}} | ||
| + | <center><math>r^2+d^2=R^2\;</math></center> | ||
| + | {{p}} | ||
| + | En el cono la sección también será un círculo y ahora el radio es aún más fácil de determinar (como el radio de apertura del cono es de 45º, resulta que el radio es d). | ||
| + | {{p}} | ||
| + | <center><math>Secci\acute{o}n\,_{Cilindro}=\pi R^2=\pi (r^2+d^2)=\pi r^2 + \pi d^2 = Secci\acute{o}n\,_{Esfera}+Secci\acute{o}n\,_{Cono}\;</math></center> | ||
| + | {{p}} | ||
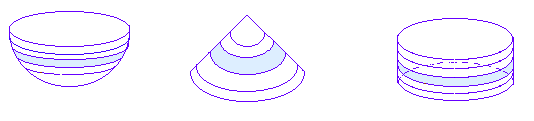
| + | Las secciones son como rebanadas de las tres figuras obtenidas cortando paralelamente a la base del cilindro. Resulta que, colocando las tres figuras como las hemos puesto y cortándolas en rebanadas finas | ||
| + | {{p}} | ||
| + | [[Imagen:esfera_cilindro_3.png|center]] | ||
| + | {{p}} | ||
| + | <center>Rebanada en cilindro = Rebanada en semiesfera + Rebanada en cono (a la misma altura)</center> | ||
| + | {{p}} | ||
| + | Si para cada altura se tiene esta relación, parece bastante claro que: | ||
| + | {{p}} | ||
| + | <center><math>V_{cilindro} = V_{semiesfera} + V_{cono}\;</math> </center> | ||
| + | {{p}} | ||
| + | Pero como: | ||
| + | |||
| + | <center><math>V_{cilindro} = \pi R^3 \qquad y \qquad V_{cono}= \cfrac{1}{3} \pi R^3</math></center> | ||
| + | |||
| + | resulta: | ||
| + | |||
| + | <center><math>V_{semiesfera} = \cfrac{2}{3} \pi R^3 \ \rightarrow \ V_{esfera} = \cfrac{4}{3} \pi R^3</math> </center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:13 1 dic 2016
|
|
En esta escena podrás calcular el volumen y área de un balón de futbol.
Teorema
El volumen de la esfera es igual a dos tercios del volumen del cilindro circunscrito a ella.
El cálculo del volumen de la esfera fue uno de los descubrimientos que Arquímedes más estimaba de todos los que hizo en su vida. Llegó a demostrar de un modo muy original que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella. Tanto le impresionó esto a él mismo que mandó que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas.
Vamos a ver cómo llegó hasta ahí. Arquímedes se imaginó una semiesfera y junto a ella un cilindro circular recto y un cono recto, ambos de base igual a un círculo máximo de la semiesfera:
Arquímedes cortó las tres figuras por un plano paralelo a la base del cilindro y cono y se preguntó cómo serían las secciones determinadas por este plano en cilindro, semiesfera y cono. En el cilindro es un círculo de radio R. En la esfera también será un círculo, pero su radio dependerá de la distancia d. Mirando la figura y acordándote del teorema de Pitágoras, fácilmente puedes escribir que si el radio de la sección es r, entonces
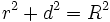
En el cono la sección también será un círculo y ahora el radio es aún más fácil de determinar (como el radio de apertura del cono es de 45º, resulta que el radio es d).
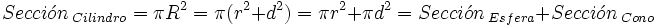
Las secciones son como rebanadas de las tres figuras obtenidas cortando paralelamente a la base del cilindro. Resulta que, colocando las tres figuras como las hemos puesto y cortándolas en rebanadas finas
Si para cada altura se tiene esta relación, parece bastante claro que:
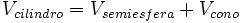
Pero como:
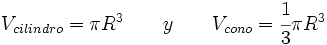
resulta:
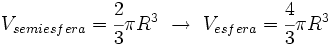
En esta escena podrás comprobar la relación que existe entre los volúmenes de la esfera, el cono y el cilindro.
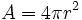
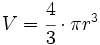
 : radio.
: radio.