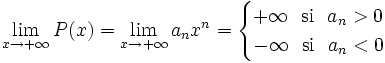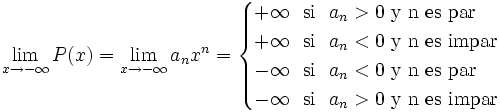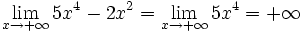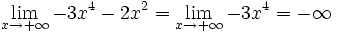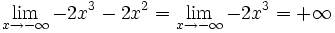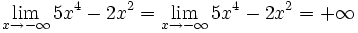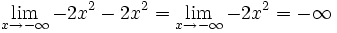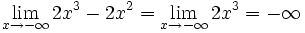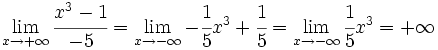Plantilla:Límite de funciones polinómicas cuando x tiende a infinito
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 05:29 18 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 21: | Línea 21: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| - | *<math>\lim_{x \to + \infty} 5x^4-2x^2 = + \infty</math> | + | *<math>\lim_{x \to + \infty} 5x^4-2x^2 = \lim_{x \to + \infty} 5x^4 = + \infty</math> |
| - | *<math>\lim_{x \to + \infty} -3x^4-2x^2 = - \infty</math> | + | *<math>\lim_{x \to + \infty} -3x^4-2x^2 = \lim_{x \to + \infty} -3x^4= - \infty</math> |
| - | *<math>\lim_{x \to - \infty} -2x^3-2x^2 = + \infty</math> | + | *<math>\lim_{x \to - \infty} -2x^3-2x^2 = \lim_{x \to - \infty} -2x^3 = + \infty</math> |
| - | *<math>\lim_{x \to - \infty} 5x^4-2x^2 = + \infty</math> | + | *<math>\lim_{x \to - \infty} 5x^4-2x^2 = \lim_{x \to - \infty} 5x^4-2x^2 = + \infty</math> |
| - | *<math>\lim_{x \to - \infty} -2x^2-2x^2 = - \infty</math> | + | *<math>\lim_{x \to - \infty} -2x^2-2x^2 = \lim_{x \to - \infty} -2x^2 = - \infty</math> |
| - | *<math>\lim_{x \to - \infty} 2x^3-2x^2 = - \infty</math> | + | *<math>\lim_{x \to - \infty} 2x^3-2x^2 = \lim_{x \to - \infty} 2x^3 = - \infty</math> |
| + | |||
| + | *<math>\lim_{x \to + \infty} \cfrac{x^3-1}{-5} = \lim_{x \to - \infty} -\cfrac{1}{5}x^3 + \cfrac{1}{5} = \lim_{x \to - \infty} \cfrac{1}{5}x^3 = + \infty</math> | ||
| }} | }} | ||
| Línea 45: | Línea 47: | ||
| {{Video_enlace_LaMejorAsesoríaEducativa | {{Video_enlace_LaMejorAsesoríaEducativa | ||
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| - | |duracion=9'59" | + | |duracion=15'57" |
| |sinopsis=Otra forma de calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞). También se incluyen otros casos de funciones radicales que tienen un tratamiento similar. | |sinopsis=Otra forma de calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞). También se incluyen otros casos de funciones radicales que tienen un tratamiento similar. | ||
| |url1=https://youtu.be/SjvDGeueUBc?list=PLyC1b2B57_HFW-7Heqe9j0gMggFTSUSOZ | |url1=https://youtu.be/SjvDGeueUBc?list=PLyC1b2B57_HFW-7Heqe9j0gMggFTSUSOZ | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=12'02" | ||
| + | |sinopsis=Ejercicios de límites de funciones polinómicas. | ||
| + | |url1=https://youtu.be/YwOBnHe1sz8 | ||
| + | }} | ||
| + | {{Video_enlace_TodoSobresaliente | ||
| + | |titulo1=Ejercicios 2 | ||
| + | |duracion=8'05" | ||
| + | |sinopsis=Ejercicios de límites de funciones polinómicas. | ||
| + | |url1=https://youtu.be/4THTCge1sKk | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
Observa cómo el valor del límite sólo depende del término de mayor grado del polinomio P(x).
Al calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞) sólo debes preocuparte del sumando de mayor grado, pues es él quien corta el bacalao.
Otra forma de calcular el límite de un polinomio en el infinito (x → +∞ ó x → -∞). También se incluyen otros casos de funciones radicales que tienen un tratamiento similar.
Ejercicios de límites de funciones polinómicas.
Ejercicios de límites de funciones polinómicas.
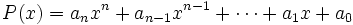 una función polinómica en la variable x, de grado n.
una función polinómica en la variable x, de grado n.