Plantilla:Relación entre las áreas y los volúmenes de dos figuras semejantes
De Wikipedia
| Revisión de 16:43 19 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:47 19 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 47: | Línea 47: | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena7/2quincena7_contenidos_2d.htm | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena7/2quincena7_contenidos_2d.htm | ||
| }} | }} | ||
| - | {{Videotutoriales|titulo=Problemas|enunciado= | + | {{Videotutoriales|titulo=Problemas: ''Relación entre las áreas de dos figuras semejantes''|enunciado= |
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| |titulo1=Problema 1 | |titulo1=Problema 1 | ||
| Línea 62: | Línea 62: | ||
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| |titulo1=Problema 3 | |titulo1=Problema 3 | ||
| + | |duracion=2'47" | ||
| + | |url1=https://www.youtube.com/watch?v=Tnthw2u4GTk | ||
| + | |sinopsis=Dos hexágonos regulares tienen sus lados en proporción 1/3. El área del mayor es 117 cm<up>2</sup>. ¿Cuánto vale el área del menor? | ||
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Problemas: ''Relación entre los volúmenes de dos figuras semejantes''|enunciado= | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Problema 1 | ||
| |duracion=4'20" | |duracion=4'20" | ||
| |url1=https://www.youtube.com/watch?v=vSUetFMeQtU | |url1=https://www.youtube.com/watch?v=vSUetFMeQtU | ||
| Línea 67: | Línea 75: | ||
| }} | }} | ||
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| - | |titulo1=Problema 4 | + | |titulo1=Problema 2 |
| |duracion=3'59" | |duracion=3'59" | ||
| |url1=https://www.youtube.com/watch?v=fkqGmFldNO4 | |url1=https://www.youtube.com/watch?v=fkqGmFldNO4 | ||
| Línea 73: | Línea 81: | ||
| }} | }} | ||
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| - | |titulo1=Problema 5 | + | |titulo1=Problema 3 |
| |duracion=3'54" | |duracion=3'54" | ||
| |url1=https://www.youtube.com/watch?v=y7ZBa-8_7Fg | |url1=https://www.youtube.com/watch?v=y7ZBa-8_7Fg | ||
Revisión de 16:47 19 sep 2017
Propiedades
Si dos figuras son semejantes y k es la constante de proporcionalidad, entonces:
- La razón entre sus áreas es k2.
- La razón entre sus volúmenes k3.
Ejemplos: Relación entre las áreas y los volúmenes de dos figuras semejantes
- Comprueba que si un cuadrado tiene 5 cm de lado y el de otro cuadrado mide el doble, 10 cm, entonces el área de éste es el cuádruple de la del primero.
- Comprueba que si un cubo tiene 5 cm de arista y la de otro cubo mide el doble, 10 cm, entonces el volumen de éste es 8 veces la del primero.
Solución 1:
En efecto, como la razón entre los lados es 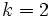 , la razón entre sus áreas es
, la razón entre sus áreas es 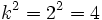 .
.
Si hallamos el área de cada cuadrado lo podremos comprobar:
- Área cuadrado pequeño=
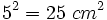
- Área cuadrado grande=
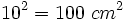
En efecto, el área del grande es el cuádruple del área del pequeño.
Solución 2:
En efecto, como la razón entre las aristas es 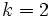 , la razón entre sus volúmenes es
, la razón entre sus volúmenes es 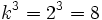 .
.
Si hallamos los volúmenes de cada cubo lo podremos comprobar:
- Volumen cubo pequeño=
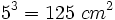
- Volumen cubo grande=
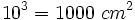
|
Ejercicio: Relación entre las áreas de dos figuras semejantes En una pizzería, la pizza pequeña tiene 23 cm de diámetro y es para una persona. Sin embargo, la pizza familiar tiene 46 cm de diámetro, justo el doble que la pequeña, pero dicen que es para 4 personas. ¿Nos están engañando? La respuesta en la siguiente actividad: |
Actividades en las que podrás ver la relación que existe entre las áreas de dos figuras semejantes.
Un pintor pinta un boceto de un mural que ocupa 2 m2. Una vez acabado, el mural ha de ocupar una superficie de 50 m2. ¿Cuál es la razón de semejanza que hay entre el mural y el boceto?
La altura de un triángulo mide 10 cm y la base 6 cm. ¿Qué área tendrá un triángulo mayor semejante a éste con una razón de semejanza iguala a 4?
Dos hexágonos regulares tienen sus lados en proporción 1/3. El área del mayor es 117 cm<up>2</sup>. ¿Cuánto vale el área del menor?
Tenemos un cubo con un volumen de 32 cm3 y otro cubo con un volumen de 12 cm3. ¿Qué relación tienen las aristas y las superficies, respectivamente?
Un cono tiene una base de radio 3 cm y su altura es de 8 cm. Por otro lado, tenemos otro cono con un radio de la base de 6 cm y altura 16 cm. Indica si son semejantes ambos conos y, en tal caso, calcula la razón de semejanza y la razón entre sus volúmenes.
Una pelota de jugar a la petanca tiene un diámetro de 10 cm, y una pelota de ping-pong tiene un diámetro de 4 cm. Calcula la razón entre sus volúmenes.

