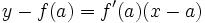Plantilla:Utilidad de la derivada (1ºBach)
De Wikipedia
| Revisión de 08:40 19 ene 2017 Coordinador (Discusión | contribuciones) (→Problemas de optimización) ← Ir a diferencia anterior |
Revisión de 09:00 19 ene 2017 Coordinador (Discusión | contribuciones) (→Problemas de optimización) Ir a siguiente diferencia → |
||
| Línea 77: | Línea 77: | ||
| {{Ejemplo|titulo=Actividades: ''Problemas de optimización'' | {{Ejemplo|titulo=Actividades: ''Problemas de optimización'' | ||
| |enunciado=[[Imagen:optimizacion1.gif|left]]'''Problema 1:''' Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | |enunciado=[[Imagen:optimizacion1.gif|left]]'''Problema 1:''' Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | ||
| + | {{p}} | ||
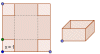
| + | [[Imagen:optimizacion2.gif|left]]'''Problema 2:''' Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo. | ||
| + | {{p}} | ||
| {{p}} | {{p}} | ||
| Línea 82: | Línea 85: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=[[Imagen:optimizacion1.gif|left]]Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | |descripcion=[[Imagen:optimizacion1.gif|left]]Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | ||
| + | |||
| |enlace=[https://ggbm.at/sbj2KdAK Solución al problema 1] | |enlace=[https://ggbm.at/sbj2KdAK Solución al problema 1] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=[[Imagen:optimizacion2.gif|left]]Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo. | ||
| + | |||
| + | |enlace=[https://ggbm.at/ZPZQVgkS Solución al problema 2] | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{AI2|titulo=Actividades interactivas: ''Problemas de optimización''|cuerpo= | {{AI2|titulo=Actividades interactivas: ''Problemas de optimización''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=[[Imagen:optimizacion1.gif|left]]'''Problema 1:''' Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | Observa la figura. Mueve el punto verde y observa los cambios: | ||
| - | *¿Qué representa el punto rojo de la izquierda?: ¿Qué relación hay entre sus coordenadas y el problema? | ||
| - | Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde: | ||
| - | *¿Qué punto de la gráfica resultante corresponderá a la solución del problema? | ||
| - | *Compruébalo activando la casilla "Ver solución". | ||
| - | Repite el proceso para un triángulo de 6 cm de base y 5 cm de altura. | ||
| - | |||
| - | Experimenta e intenta encontrar alguna regularidad en las soluciones. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/optimiza_1.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/optimiza_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | |||
| - | }} | ||
| - | {{ai_cuerpo | ||
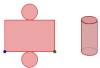
| - | |enunciado=[[Imagen:optimizacion2.gif|left]]'''Problema 2:''' Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo. | ||
| - | {{p}} | ||
| - | |||
| - | |actividad= | ||
| - | Observa la figura. Mueve el punto verde y observa los cambios: | ||
| - | *¿Qué representa el punto rojo de la izquierda?: ¿Qué relación hay entre sus coordenadas y el problema? | ||
| - | |||
| - | Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde: | ||
| - | *¿Qué punto de la gráfica resultante corresponderá a la solución del problema? | ||
| - | |||
| - | Repite el proceso para una cartulina cuadrada de 4 cm de lado. | ||
| - | |||
| - | ¿Y si la cartulina es un rectángulo de dimensiones 8x5 cm? | ||
| - | |||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/optimiza_2.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/optimiza_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | ---- | ||
| - | |||
| - | '''GUIÓN DE TRABAJO:''' | ||
| - | [[Imagen:optimiza_2.gif|right]] | ||
| - | #Observa la figura. Si decidimos cortar cuadrados de 15 cm de lado en las esquinas de las láminas metálicas, determina las dimensiones y el volumen (en litros) que tendrá la caja que formaremos al doblar las pestañas. | ||
| - | #¿Cómo cambiarían esas dimensiones si los cuadrados que cortamos son de 12 cm de lado? | ||
| - | #Si cortamos cuadrados más pequeños, ¿obtenemos necesariamente cajas de un volumen mayor? Explica tu respuesta | ||
| - | #Como la profesora Pérez quiere obtener cajas con el volumen más grande posible, ¿se te ocurre alguna manera de determinar la medida del cuadrado que cortaremos para lograr ese mayor volumen? | ||
| - | #Encuentra una expresión algebraica que permita conocer el volumen (en litros) de la caja a partir de su altura, es decir, del lado del cuadrado recortado (en dm). | ||
| - | #Construye una tabla de valores a partir de la fórmula obtenida. | ||
| - | #Observa la figura interactiva de debajo. Mueve el punto verde y comprueba si tienes errores en la tabla de valores. | ||
| - | #Explica el significado del punto rojo y su variación al mover el verde. | ||
| - | #Justifica o niega las siguientes afirmaciones, razonando tu respuesta: | ||
| - | ##El volumen de la caja aumenta y disminuye al incrementar la altura de la caja. | ||
| - | ##Es imposible hallar el volumen de una caja conociendo sólo una de sus tres dimensiones. | ||
| - | ##La relación entre la altura de una caja y su volumen es lineal. | ||
| - | #Vamos a representar gráficamente la función definida en la cuestión nº 5: haz clic derecho sobre el punto rojo y "activa la traza". Luego vuelve a mover el punto verde. Describe lo que ocurre. | ||
| - | #¿Cuál es el dominio de la función? ¿Por qué? | ||
| - | #¿En qué punto se alcanza el valor más alto de la gráfica? Compruébalo mediante el deslizador de "Ver solución" | ||
| - | #Cómo será la tangente a la gráfica en ese punto? Compruébalo mediante el deslizador de "Ver tangente" | ||
| - | #¿Cuál será el valor de su pendiente? ¿Qué relación tiene ese valor con la derivada de la función en ese punto? | ||
| - | #Toma la función definida en la cuestión 5 para el volumen y calcula su función derivada. | ||
| - | #Sustituye en ella la x por el valor dado para la solución. ¿Cuánto da? | ||
| - | #Resume tus conclusiones: ¿cómo se puede calcular el valor máximo o minimo de una función? | ||
| - | |||
| - | |||
| - | ''Adaptado por Manuel Sada Allo (Abri 2006) a partir de la propuesta: Lupiáñez, J.L. y Codina, A. (2002). Implementando problemas de optimización con calculadora gráica. Trabajo presentado en el X Congreso sobre Enseñanza y Aprendizaje de las Matemáticas. El Ejido, Almería.a partir de una actividad de Jose Luis Lupiáñez Gómez y Antonio Codina Sánchez'' | ||
| - | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| |enunciado=[[Imagen:optimizacion3.gif|left]]'''Problema 3a:''' Queremos construir una lata de un tercio de litro de capacidad. | |enunciado=[[Imagen:optimizacion3.gif|left]]'''Problema 3a:''' Queremos construir una lata de un tercio de litro de capacidad. | ||
Revisión de 09:00 19 ene 2017
Tabla de contenidos |
Cálculo de la ecuación de la recta tangente
Proposición
La ecuación de la recta tangente a la curva  en un punto de abscisa
en un punto de abscisa  viene dada por la ecuación:
viene dada por la ecuación:
|
|
En esta escena podrás calcular la ecuación de la recta tangente a una curva dada su ecuación.
Estudio del crecimiento
Procedimiento
Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:
- En aquellos puntos donde la derivada sea positiva la función será creciente.
- En aquellos puntos donde la derivada sea negativa la función será decreciente.
Estudio de los puntos singulares
Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.
Esos puntos pueden ser máximos o mínimos, pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.
Problemas de optimización
Un problema de optimización es aquél en el que se pretende averiguar el máximo o el mínimo de una magnitud dada.
Por ejemplo, encontrar el área mínima, el menor coste, la forma óptima, la menor resistencia, el máximo beneficio, el mayor alcance...
Procedimiento
- Identifica todas las cantidades dadas y las cantidades a determinar.
- Escribe una ecuación primaria para la magnitud que debe hacerse máxima o mínima.
- Reduce la ecuación primaria a una ecuación que sólo tenga una variable independiente. Este paso te puede exigir el utilizar ecuaciones secundarias que relacionen las variables independientes de la ecuación primaria. (Las despejas en las secundarias y las sustituyes en la primaria)
- Fija el dominio de la ecuación primaria. Ésto es, determina el rango de valores para los que tiene sentido el problema planteado.
- Obtén el valor máximo o mínimo solicitado mediante el estudio de los ceros y del crecimiento de la función derivada.
- Introducción a los problemas de optimización.
- Ejemplo 1: Hallar el punto de la parábola
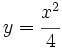 más próximo al punto (-1,2).
más próximo al punto (-1,2).
- Ejemplo 2: Hallar el punto de la curva
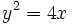 más próximo al punto (2,-1).
más próximo al punto (2,-1).
Actividades: Problemas de optimización
Problema 1: Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). Problema 2: Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo.
|
Actividades interactivas: Problemas de optimización
Problema 3a: Queremos construir una lata de un tercio de litro de capacidad.
¿Cuáles serán las dimensiones de la lata más barata (en cuanto a superficie de hojalata)?.
Problema 3a: ¿Y si la hojalata para las tapas cuesta el doble que la destinada a la cara lateral? Actividad: Problema 3a: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 3b:
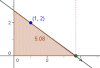
Problema 4a: De todas las rectas que pasan por el punto (1,2), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima.
Problema 4b: De todas las rectas que pasan por el punto (a,b), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima. Actividad: Problema 4a: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 4b: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Cambia el punto de apoyo de las rectas (inicialmente (3,1)) por otro y observa cómo varía la solución:
Problema 5: Un triángulo isósceles tiene el lado desigual de 12 cm y la altura relativa a ese lado de 5 cm. Encontrar un punto sobre la altura tal que la suma de distancias a los tres vértices sea mínima..
Actividad: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 6: Dada la función definida en el intervalo [1,e] por
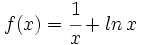 , determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente. , determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente.
Actividad: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
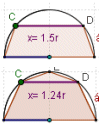
Problema 7a: En una semicircunferencia de diámetro AB=2r se traza una cuerda CD paralela a AB. ¿Cuál debe ser la longitud de esa cuerda para que el área del trapecio ABDC sea máxima?
Actividad: Problema 7a: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 7b: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 8a: Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a 3 km/h y corre por la arena a 10 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible.
Problema 8b: Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a v1 km/h y corre por la arena a v2 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible. Actividad: Problema 8a: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 8b: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 9a: Divide el número 8 en dos partes de manera que su producto multiplicado por la diferencia entre las partes sea tan grande como sea posible.
Problema 9b: Divide el número n en dos partes de manera que su producto multiplicado por la diferencia entre las partes sea tan grande como sea posible.(Este es uno de los problemas que Ferrari puso a Tartaglia en su histórico duelo de problemas)
Actividad: Problema 9a: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Problema 9b: Observa la figura. Elige un valor para n (mediante el correspondiente deslizador). Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
|
Aplicación al cálculo de límites: Regla de L'Hopital
Para ampliar
Calculo de la variación porcentual.