Plantilla:Utilidad de la derivada (1ºBach)
De Wikipedia
| Revisión de 11:03 3 may 2017 Coordinador (Discusión | contribuciones) (→Cálculo de la ecuación de la recta tangente a una curva) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Cálculo de la ecuación de la recta tangente a una curva) |
||
| Línea 51: | Línea 51: | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales | ||
| + | |titulo=Ejercicios: ''Ecuación de la recta tangente y de la recta normal'' | ||
| + | |enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=11'54" | ||
| + | |sinopsis=Cómo se halla la recta tangente a una curva. Ejemplos. | ||
| + | |url1=https://youtu.be/7tU2EZdVlmo?list=PLwCiNw1sXMSC8-MgHpDRjIsMzs9qVJSwU | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=10'49" | ||
| + | |sinopsis=Más ejemplos del cálculo de la recta tangente a una curva. | ||
| + | |url1=https://youtu.be/217bHpdLKF8?list=PLwCiNw1sXMSC8-MgHpDRjIsMzs9qVJSwU | ||
| + | }} | ||
| + | ---- | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 1 | + | |titulo1=Ejercicio 1 |
| |duracion=6'12" | |duracion=6'12" | ||
| |sinopsis=Halla la ecuación de la recta tangente a la curva <math>y=\cfrac{1}{x-2}\,</math> en el punto <math>P(4,\frac{1}{2})</math>. | |sinopsis=Halla la ecuación de la recta tangente a la curva <math>y=\cfrac{1}{x-2}\,</math> en el punto <math>P(4,\frac{1}{2})</math>. | ||
| Línea 58: | Línea 74: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 2 | + | |titulo1=Ejercicio 2 |
| |duracion=12'10" | |duracion=12'10" | ||
| |sinopsis=Halla la ecuación de la recta tangente a la curva <math>y=3x^2\,ln\,x\, + 4x\,</math> en el punto de abscisa 1. | |sinopsis=Halla la ecuación de la recta tangente a la curva <math>y=3x^2\,ln\,x\, + 4x\,</math> en el punto de abscisa 1. | ||
| Línea 64: | Línea 80: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 3 | + | |titulo1=Ejercicio 3 |
| |duracion=14'28" | |duracion=14'28" | ||
| - | |sinopsis=Halla la ecuación de la recta normal a la curva <math>y=\cfrac{3x-1}{x^+1}\,</math> en el punto de abscisa 3. | + | |sinopsis=Halla la ecuación de la recta normal a la curva <math>y=\cfrac{3x-1}{x+1}\,</math> en el punto de abscisa 3. |
| |url1=https://www.youtube.com/watch?v=O5Y0qwxC8Ww | |url1=https://www.youtube.com/watch?v=O5Y0qwxC8Ww | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=8'23" | ||
| + | |sinopsis=Halla la ecuación de la recta normal y tangente a la curva <math>y=x^3+1\,</math> en el punto de abscisa 1. | ||
| + | |url1=https://www.youtube.com/watch?v=H3Ydr96kbUA | ||
| }} | }} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo: Ecuación de la recta tangente | + | |titulo1=Ejercicio 5 |
| |duracion=7'38" | |duracion=7'38" | ||
| |sinopsis=Hallas las coordenadas del punto de la curva <math>y=x^2\;</math> en el que la recta tangente es paralela a la bisectriz del primer cuadrante. | |sinopsis=Hallas las coordenadas del punto de la curva <math>y=x^2\;</math> en el que la recta tangente es paralela a la bisectriz del primer cuadrante. | ||
| |url1=http://www.unicoos.com/video/matematicas/2-bachiller/aplicaciones-de-las-derivadas/recta-tangente-y-normal/ecuacion-recta-tangente-01 | |url1=http://www.unicoos.com/video/matematicas/2-bachiller/aplicaciones-de-las-derivadas/recta-tangente-y-normal/ecuacion-recta-tangente-01 | ||
| }} | }} | ||
| - | + | {{Video_enlace_matefacil | |
| - | ==Estudio del crecimiento y de los puntos singulares== | + | |titulo1=Ejercicio 6 |
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | + | |duracion=9´38" |
| - | Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada: | + | |url1=https://www.youtube.com/watch?v=vkbhSfRXmgo&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A&index=24 |
| - | *En aquellos puntos donde la derivada sea positiva la función será creciente. | + | |sinopsis=Encontrar los vectores unitarios que son paralelos a la recta tangente a la función <math>y=x^2\;</math> en el punto (2,4). |
| - | *En aquellos puntos donde la derivada sea negativa la función será decreciente. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Funciones crecientes y decrecientes | + | |
| - | |duracion=13'02" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/19-funciones-crecientes-o-decrecientes-2#.WGObhEZ9Vko | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Criterios de crecimiento y decrecimiento | + | |
| - | |duracion=7'19" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/20-criterios-de-crecimiento-y-decrecimiento-2#.WGObmEZ9Vko | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Caja_Amarilla|texto=Se llaman '''puntos singulares''' de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | Esos puntos pueden ser máximos o mínimos, pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función. | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Determinación de los extremos relativos | + | |
| - | |duracion=13'46" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/21-maximos-y-minimos-relativos-o-locales-2#.WGObq0Z9Vko | + | |
| }} | }} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Determinación de máximos y mínimos absolutos | ||
| - | |duracion=14'45" | ||
| - | |sinopsis= | ||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/22-determinacion-de-maximos-y-minimos-absolutos-2#.WGOb2UZ9Vko | ||
| }} | }} | ||
| - | {{p}} | + | ==Estudio del crecimiento y de los puntos singulares== |
| - | {{Ejemplo | + | {{Estudio del crecimiento y de los puntos singulares}} |
| - | |titulo=Ejercicio resuelto: ''Puntos singulares y crecimiento'' | + | |
| - | |enunciado=Dada la función <math>f(x)=x^3-6x^2+9x+2\;</math>, halla sus puntos singulares y estudia su crecimiento. | + | |
| - | |sol= | + | |
| - | <math>f'(x)=3x^2-12x+9\;</math> | + | |
| - | Puntos singulares: | ||
| - | |||
| - | <math>f'(x)=0 \iff 3x^2-12x+9=0 \iff x=\begin{cases} | ||
| - | x_1= 1 | ||
| - | \\ | ||
| - | x_2=3 | ||
| - | \end{cases}</math> | ||
| - | |||
| - | Para estudiar el crecicmiento determinaremos el signo de la función derivada mediante una tabla en la que estableceremos zonas delimitadas por los puntos singulares y por los puntos de discontinuidad, si los hubiese. En nuestro caso hay 3 zonas porque hay 2 puntos singulares y no hay discontinuidades, por tratarse f'(x) de una función polinómica.). | ||
| - | |||
| - | -inf 1 3 +inf | ||
| - | -----!------!-------!------! | ||
| - | f'(x)! + ! - ! + ! | ||
| - | -----!------!-------!------! | ||
| - | f(x)! Cre ! Decre ! Cre ! | ||
| - | ---------------------------- | ||
| - | |||
| - | El estudio del crecimiento nos permite determinar que (1,6) es un máximo y (3,2) es un mínimo. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo 1: Puntos singulares, crecimiento y curvatura | ||
| - | |duracion=9'54" | ||
| - | |sinopsis=Estudio de los puntos singulares, crecimiento y curvatura (concavidad) de una función polinómica. | ||
| - | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/aplicaciones-de-la-derivada/crecimiento-y-curvatura/crecimiento-y-curvatura-de-una-funcion-polinomica | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo 2: Máximos, mínimos y puntos de inflexión | ||
| - | |duracion=7'30" | ||
| - | |sinopsis=Hallar el valor de los parámetros para que se den ciertas condiciones. | ||
| - | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/aplicaciones-de-la-derivada/maximos-minimos-y-puntos-de-inflexion/maximos-minimos-y-puntos-de-inflexion | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| ==Problemas de optimización== | ==Problemas de optimización== | ||
| - | {{Caja_Amarilla|texto=Un problema de '''optimización''' es aquél en el que se pretende averiguar el máximo o el mínimo de una magnitud dada.}} | + | {{Problemas de optimización}} |
| - | {{p}} | + | |
| - | Por ejemplo, encontrar el área mínima, el menor coste, la forma óptima, la menor resistencia, el máximo beneficio, el mayor alcance... | + | |
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | + | |
| - | *Identifica todas las cantidades dadas y las cantidades a determinar. | + | |
| - | *Escribe una ecuación primaria para la magnitud que debe hacerse máxima o mínima. | + | |
| - | *Reduce la ecuación primaria a una ecuación que sólo tenga una variable independiente. Este paso te puede exigir el utilizar ecuaciones secundarias que relacionen las variables independientes de la ecuación primaria. (Las despejas en las secundarias y las sustituyes en la primaria) | + | |
| - | *Fija el dominio de la ecuación primaria. Ésto es, determina el rango de valores para los que tiene sentido el problema planteado. | + | |
| - | *Obtén el valor máximo o mínimo solicitado mediante el estudio de los ceros y del crecimiento de la función derivada. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=El verbo optimizar | + | |
| - | |duracion=09'03" | + | |
| - | |sinopsis={{p}} | + | |
| - | *Introducción a los problemas de optimización. | + | |
| - | *'''Ejemplo 1:''' Hallar el punto de la parábola <math>y=\cfrac{x^2}{4}</math> más próximo al punto (-1,2). | + | |
| - | *'''Ejemplo 2:''' Hallar el punto de la curva <math>y^2=4x\,</math> más próximo al punto (2,-1). | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/23-el-verbo-optimizar-2#.WGOb-EZ9Vko | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_unicoos | + | |
| - | |titulo1=Ejemplo: Problema de optimización | + | |
| - | |duracion=11'59" | + | |
| - | |sinopsis=Optimización del área impresa de un folio. | + | |
| - | |url1=http://www.unicoos.com/video/matematicas/2-bachiller/aplicaciones-de-las-derivadas/optimizacion/optimizacion-del-area-impresa-de-un-folio | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{ejemplo2|titulo=Actividades interactivas: ''Problemas de optimización''|enunciado= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
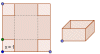
| - | [[Imagen:optimizacion1.gif|left]]'''Problema 1:''' Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo). | + | |
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/sbj2KdAK Solución al problema 1] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion2.gif|left]]'''Problema 2:''' Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo. | + | |
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar loa solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/ZPZQVgkS Solución al problema 2] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion3.gif|left]]'''Problema 3:''' Queremos construir una lata de un tercio de litro de capacidad. | + | |
| - | + | ||
| - | ¿Cuáles serán las dimensiones de la lata más barata (en cuanto a superficie de hojalata)?. | + | |
| - | {{p}} | + | |
| - | + | ||
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/s9GtX9MH Solución al problema 3] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
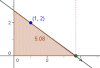
| - | |enunciado=[[Imagen:optimizacion4.gif|left]]'''Problema 4a:''' De todas las rectas que pasan por el punto (1,2), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima. | + | |
| - | '''Problema 4b:''' De todas las rectas que pasan por el punto (a,b), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima. | + | |
| - | {{p}} | + | |
| - | + | ||
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/WmrzV9SP Solución al problema 4a] | + | |
| - | }} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/wcY5GNJp Solución al problema 4b] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion5.gif|left]]'''Problema 5:''' Un triángulo isósceles tiene el lado desigual de 12 cm y la altura relativa a ese lado de 5 cm. Encontrar un punto sobre la altura tal que la suma de distancias a los tres vértices sea mínima. | + | |
| - | {{p}} | + | |
| - | + | ||
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/KFxCjkkD Solución al problema 5] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion6.gif|left]]'''Problema 6:''' Dada la función definida en el intervalo [1,e] por <math>f(x)=\cfrac{1}{x} + ln \, x</math> , determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente. | + | |
| - | {{p}} | + | |
| - | + | ||
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/Bq7UmeWa Solución al problema 6] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
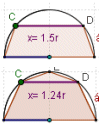
| - | |enunciado=[[Imagen:optimizacion7ab.gif|left]]'''Problema 7a:''' En una semicircunferencia de diámetro AB=2r se traza una cuerda CD paralela a AB. ¿Cuál debe ser la longitud de esa cuerda para que el área del trapecio ABDC sea máxima? | + | |
| - | {{p}} | + | |
| - | '''Problema 7b:''' En una semicircunferencia de diámetro AB=2r se traza una cuerda CD paralela a AB. Llamamos E al punto medio del arco CD y dibujamos el pentágono ACEDB. Calcula la longitud de la cuerda CD para que el área del pentágono sea máxima. | + | |
| - | {{p}} | + | |
| - | + | ||
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/jSBqGcer Solución al problema 7a] | + | |
| - | }} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/Da9JFsyb Solución al problema 7b] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion8.jpg|left]]'''Problema 8a:''' Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a 3 km/h y corre por la arena a 10 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible. | + | |
| - | {{p}} | + | |
| - | '''Problema 8b:''' Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a v1 km/h y corre por la arena a v2 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible. | + | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/NCakuuT4 Solución al problema 8a] | + | |
| - | }} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/xpCQcgmn Solución al problema 8b] | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado=[[Imagen:optimizacion9.gif|left]]'''Problema 9a:''' Divide el número 8 en dos partes de manera que su producto multiplicado por la diferencia entre las partes sea tan grande como sea posible.{{p}} | + | |
| - | {{p}} | + | |
| - | '''Problema 9b:''' Divide el número n en dos partes de manera que su producto multiplicado por la diferencia entre las partes sea tan grande como sea posible.{{p}}(Este es uno de los problemas que [[Ferrari]] puso a [[Tartaglia]] en su histórico duelo de problemas) | + | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/nSnaybEk Solución al problema 9a] | + | |
| - | }} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Escena de Geogebra para visualizar la solución del problema. | + | |
| - | + | ||
| - | |enlace=[https://ggbm.at/dWTzxSwe Solución al problema 9b] | + | |
| - | }} | + | |
| - | + | ||
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ==Aplicación al cálculo de límites: Regla de L'Hôpital== | ==Aplicación al cálculo de límites: Regla de L'Hôpital== | ||
| - | {{Teorema_sin_demo|titulo=Regla de L'Hôpital|enunciado= | + | {{Regla de LHopital}} |
| - | *Si <math>\lim_{x \to a} \cfrac{f(x)}{g(x)} </math> es una indeterminación del tipo <math>\cfrac{0}{0}</math> y <math>\lim_{x \to a} \cfrac{f'(x)}{g'(x)}=l \, ; \ (l \in \mathbb{R})</math>, entonces <math>\lim_{x \to a} \cfrac{f(x)}{g(x)}=l </math>. | + | |
| - | *Si <math>x \to +\infty</math> o <math>x \to -\infty</math>también se cumple la regla de L'Hôpital. | + | |
| - | *Si la indeterminación es del tipo <math>\cfrac{\infty}{\infty}</math> también se cumple la regla. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo | + | |
| - | |titulo=Ejercicio resuelto: ''Regla de L'Hôpital'' | + | |
| - | |enunciado=Calcula: | + | |
| - | :a)<math>\lim_{x \to 3} \cfrac{x^3-5x-12}{x^2+3x-18)} </math> | + | |
| - | :b)<math>\lim_{x \to +\infty} \cfrac{x^3}{2^x} </math> | + | |
| - | |sol= | + | |
| - | a) <math>\lim_{x \to +\infty} \cfrac{x^3}{2^x} = ind. \left( \cfrac{\infty}{\infty} \right)</math> | + | |
| - | + | ||
| - | Aplicando la regla de L'Hôpital: | + | |
| - | + | ||
| - | <math>\lim_{x \to +\infty} \cfrac{x^3}{2^x} =\lim_{x \to +\infty} \cfrac{3x^2}{2^x \, ln \, 2}=ind. \left( \cfrac{\infty}{\infty} \right) </math> | + | |
| - | + | ||
| - | Aplicando la regla de L'Hôpital otra vez: | + | |
| - | + | ||
| - | <math>\lim_{x \to +\infty} \cfrac{3x^2}{2^x \, ln \, 2} =\lim_{x \to +\infty} \cfrac{6x}{2^x \, (ln \, 2)^2}=ind. \left( \cfrac{\infty}{\infty} \right) </math> | + | |
| - | + | ||
| - | Y aplicando la regla de L'Hôpital una vez más: | + | |
| - | + | ||
| - | <math>\lim_{x \to +\infty} \cfrac{6x}{2^x \, (ln \, 2)^2} =\lim_{x \to +\infty} \cfrac{6}{2^x \, (ln \, 2)^3}=0 </math> | + | |
| - | }} | + | |
| - | + | ||
| - | ==Para ampliar== | + | |
| - | + | ||
| - | {{Video_enlace2 | + | |
| - | |titulo1=Elasticidad de una función en un punto | + | |
| - | |duracion=11'36" | + | |
| - | |sinopsis=Calculo de la variación porcentual. | + | |
| - | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones/13-elasticidad-de-una-funcion-en-un-punto#.WGOdF0Z9Vko | + | |
| - | }} | + | |
| - | + | ||
| - | {{Video_enlace2 | + | |
| - | |titulo1=Derivadas de orden superior | + | |
| - | |duracion=16'51" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones/14-derivadas-de-orden-superior#.WGOdRkZ9Vko | + | |
| - | }} | + | |
| - | + | ||
| - | {{Video_enlace2 | + | |
| - | |titulo1=Concavidad y puntos de inflexión | + | |
| - | |duracion=30'41" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/24-concavidad-y-puntos-de-inflexion-2#.WGOcJUZ9Vko | + | |
| - | }} | + | |
Revisión actual
Tabla de contenidos |
Cálculo de la ecuación de la recta tangente a una curva
Proposición
La ecuación de la recta tangente a la curva  en un punto de abscisa
en un punto de abscisa  viene dada por la ecuación:
viene dada por la ecuación:
|
|
Ejemplo: Ecuación de la recta tangente
Dada la función 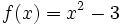 , halla la ecuación de la recta tangente en el punto
, halla la ecuación de la recta tangente en el punto 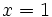 .
.
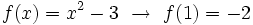
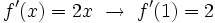
La ecuación de la recta tangente a la curva en el punto 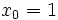 es:
es:
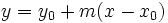
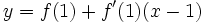
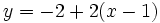
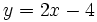
Puedes comprobar el resultado en la siguiente escena:
En esta escena podrás calcular la ecuación de la recta tangente a una curva .
Ejercicio resuelto: Ecuación de la recta tangente
Dada la función 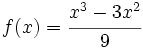 , halla las ecuaciones de la rectas tangentes que sean paralelas a la bisectriz del primer cuadrante.
, halla las ecuaciones de la rectas tangentes que sean paralelas a la bisectriz del primer cuadrante.
Hay dos soluciones:
Puedes comprobar el resultado en la siguiente escena:
En esta escena podrás calcular la ecuación de la recta tangente a una curva .
Cómo se halla la recta tangente a una curva. Ejemplos.
Más ejemplos del cálculo de la recta tangente a una curva.
Halla la ecuación de la recta tangente a la curva 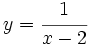 en el punto
en el punto 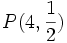 .
.
Halla la ecuación de la recta tangente a la curva 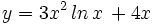 en el punto de abscisa 1.
en el punto de abscisa 1.
Halla la ecuación de la recta normal a la curva 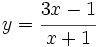 en el punto de abscisa 3.
en el punto de abscisa 3.
Halla la ecuación de la recta normal y tangente a la curva 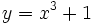 en el punto de abscisa 1.
en el punto de abscisa 1.
Hallas las coordenadas del punto de la curva 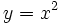 en el que la recta tangente es paralela a la bisectriz del primer cuadrante.
en el que la recta tangente es paralela a la bisectriz del primer cuadrante.
Encontrar los vectores unitarios que son paralelos a la recta tangente a la función 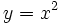 en el punto (2,4).
en el punto (2,4).
Estudio del crecimiento y de los puntos singulares
Procedimiento
Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:
- En aquellos puntos donde la derivada sea positiva la función será creciente.
- En aquellos puntos donde la derivada sea negativa la función será decreciente.
Funciones crecientes y decrecientes
Criterios de crecimiento y decrecimiento
Estudia el crecimiento de 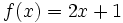
Estudia el crecimiento de 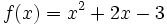
Estudia el crecimiento de 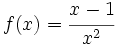
Demuestra que 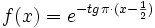 es positiva y decreciente en el intervalo (0,1).
es positiva y decreciente en el intervalo (0,1).
Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.
Esos puntos pueden ser puntos extremos (máximos o mínimos), pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.
Monotonía y extremos relativos
Monotonía y extremos relativos.Ejemplos
¿Qué son los puntos máximos, mínimos, locales y globales, crecimiento y decrecimiento?
Determinación de los extremos relativos
Determinación de máximos y mínimos absolutos
Estudia el crecimiento y los puntos extremos de 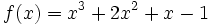
Estudia el crecimiento y los puntos extremos de 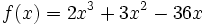
Estudia el crecimiento y los puntos extremos de 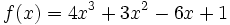
Estudia el crecimiento y los puntos extremos de 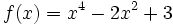
Halla los máximos y mínimos de 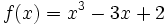
Encuentra el valor de "k" tal que 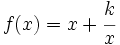 tenga un máximo local en x=-2.
tenga un máximo local en x=-2.
Halla los máximos y mínimos de 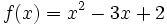
Halla los máximos y mínimos de 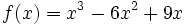
Halla los máximos y mínimos de 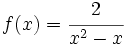
Halla los máximos y mínimos de 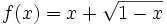
Halla los máximos y mínimos de 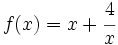
Ejercicio resuelto: Puntos singulares y crecimiento
Dada la función 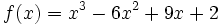 , halla sus puntos singulares y estudia su crecimiento.
, halla sus puntos singulares y estudia su crecimiento.
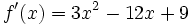
Puntos singulares:
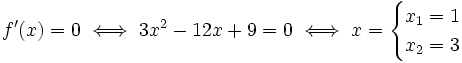
Para estudiar el crecimiento determinaremos el signo de la función derivada mediante una tabla en la que estableceremos zonas delimitadas por los puntos singulares y por los puntos de discontinuidad, si los hubiese. En nuestro caso hay 3 zonas porque hay 2 puntos singulares y no hay discontinuidades, por tratarse f'(x) de una función polinómica.
-inf 1 3 +inf
-----!------!-------!------!
f'(x)! + ! - ! + !
-----!------!-------!------!
f(x)! Cre ! Decre ! Cre !
----------------------------
Como f(1)=6 y f(3)=2, el anterior análisis del crecimiento nos permite determinar que (1,6) es un máximo y (3,2) es un mínimo.|
Actividad: Extremos relativos Nota para los cursos de secundaria: Algunas de las siguientes actividades son sólo ilustrativas ya que su resolución manual requiere conocimientos de 1º de bachillerato.
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Problemas de optimización
Un problema de optimización es aquél en el que se pretende averiguar el máximo o el mínimo de una magnitud dada.
Por ejemplo, encontrar el área mínima, el menor coste, la forma óptima, la menor resistencia, el máximo beneficio, el mayor alcance...
Procedimiento
- Identifica todas las cantidades dadas y las cantidades a determinar.
- Escribe una ecuación primaria para la magnitud que debe hacerse máxima o mínima.
- Reduce la ecuación primaria a una ecuación que sólo tenga una variable independiente. Este paso te puede exigir el utilizar ecuaciones secundarias que relacionen las variables independientes de la ecuación primaria. (Las despejas en las secundarias y las sustituyes en la primaria)
- Fija el dominio de la ecuación primaria. Ésto es, determina el rango de valores para los que tiene sentido el problema planteado.
- Obtén el valor máximo o mínimo solicitado mediante el estudio de los ceros y del crecimiento de la función derivada.
- Introducción a los problemas de optimización.
- Ejemplos.
Problemas de optimización. Ejemplos
- Introducción a los problemas de optimización.
- Ejemplo 1: Hallar el punto de la parábola
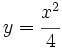 más próximo al punto (-1,2).
más próximo al punto (-1,2).
- Ejemplo 2: Hallar el punto de la curva
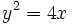 más próximo al punto (2,-1).
más próximo al punto (2,-1).
Problemas de optimización.
- Determina el punto Q de la parábola
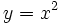 más próximo al punto P(3,0).
más próximo al punto P(3,0).
- Comprueba que la recta QP es perpendicular a la tangente a la parábola en Q.
De todas las rectas del plano que pasan por el punto (1, -3), determina la que forma un triángulo de área mínima con la parte positiva del eje de abscisas y la negativa del eje de ordenadas.
El coste total (en miles de pesos) de pedido y almacenaje de x automóviles es
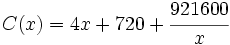
Determina el tamaño del pedido que minimiza el coste total.
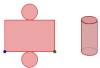
Una ventana tiene forma de rectángulo coronado por un triángulo equilátero. Encuentra las dimensiones del rectángulo para que la ventana permita la máxima entrada de luz, si el perímetro de la misma debe ser 12 metros.
Se necesita construir una caja sin tapa con una lámina rectangular de largo 24 cm y ancho 12 cm. ¿Cuál es la medida del lado del cuadrado que debe cortarse en cada esquina para maximizar el volumen de la caja? ¿Cuál es el valor de dicho volumen máximo?.
Optimización del área impresa de un folio bajo ciertas condiciones.
Actividades interactivas: Problemas de optimización
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar loa solución del problema.
¿Cuáles serán las dimensiones de la lata más barata (en cuanto a superficie de hojalata)?.
Escena de Geogebra para visualizar la solución del problema.
Problema 4b: De todas las rectas que pasan por el punto (a,b), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
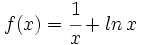 , determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente.
, determina cuáles de las rectas tangentes a su gráfica tiene la máxima pendiente.
Escena de Geogebra para visualizar la solución del problema.
Problema 7b: En una semicircunferencia de diámetro AB=2r se traza una cuerda CD paralela a AB. Llamamos E al punto medio del arco CD y dibujamos el pentágono ACEDB. Calcula la longitud de la cuerda CD para que el área del pentágono sea máxima.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Problema 8b: Un nadador, A, se encuentra a 3 km de la playa en frente de una caseta (C). Desea ir a B, en la misma playa, a 6 km de la caseta. Sabiendo que nada a v1 km/h y corre por la arena a v2 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Escena de Geogebra para visualizar la solución del problema.
Aplicación al cálculo de límites: Regla de L'Hôpital
Regla de L'Hôpital
Si al calcular 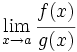 se presenta una indeterminación del tipo
se presenta una indeterminación del tipo 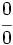 ó
ó 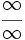 , y
, y 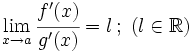 , entonces
, entonces 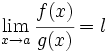 .
.
Esto también es cierto si  o
o 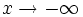 .
.
- Demostración de la regla de l'Hopital para el caso de indeterminación 0/0.
- Ejemplos de aplicación de la regla.
- Ejemplos en los que no se puede aplicar la regla por no verificarse las condiciones.
Ejercicio resuelto: Regla de L'Hôpital
Calcula:
- a)
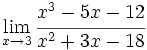
- b)
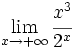
- c)
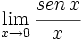
a) 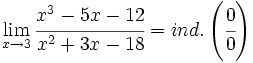
Aplicando la regla de L'Hôpital:
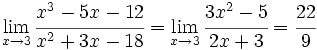
b) 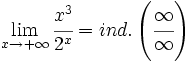
Aplicando la regla de L'Hôpital:
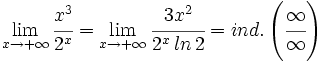
Aplicando la regla de L'Hôpital otra vez:
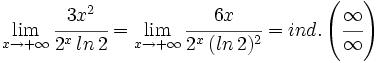
Y aplicando la regla de L'Hôpital una vez más:
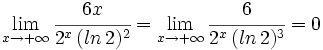
c)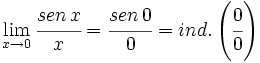
Aplicando la regla de L'Hôpital:
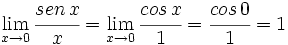
Regla de l'Hopital para los casos de indeterminación básicos. Ejemplos.
Regla de l'Hopital para todos los casos de indeterminación. Ejemplos.
Calcula: 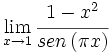
Calcula: 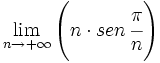
Calcula: 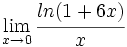
Calcula: 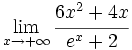
Calcula: 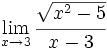
Calcula: 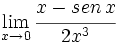
Calcula: 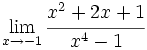
Regla de l'Hopital. Ejemplos en los que hay que aplicarla varias veces.
Calcula: 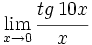
Calcula: 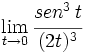
Calcula: 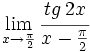
Calcula: 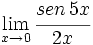
Calcula: 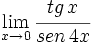
Calcula: 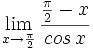
Calcula: 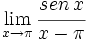
Calcula: 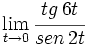
Calcula: 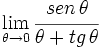
Calcula: 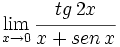
Calcula: 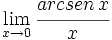
Calcula: 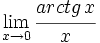
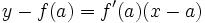
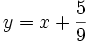
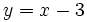
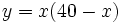
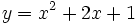
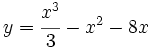 .
.