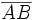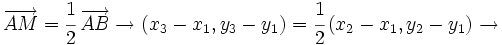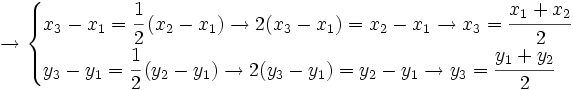Puntos y vectores el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:07 17 mar 2009 Coordinador (Discusión | contribuciones) (→Punto medio de un segmento) ← Ir a diferencia anterior |
Revisión de 08:08 17 mar 2009 Coordinador (Discusión | contribuciones) (→Punto medio de un segmento) Ir a siguiente diferencia → |
||
| Línea 60: | Línea 60: | ||
| <center><math>M=\Big( \cfrac{x_1+x_2}{2}, \cfrac{y_1+y_2}{2} \Big)</math></center> | <center><math>M=\Big( \cfrac{x_1+x_2}{2}, \cfrac{y_1+y_2}{2} \Big)</math></center> | ||
| |demo= | |demo= | ||
| - | [[Imagen:puntomedio.gif|right]]Sea <math>M=(x_3,y_3)\,</math> el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AB}</math>}}. Tenemos que: | + | [[Imagen:puntomedio.gif|right]] |
| + | :Sea <math>M=(x_3,y_3)\,</math> el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AB}</math>}}. Tenemos que: | ||
| {{p}} | {{p}} | ||
| - | :<math>\overrightarrow{AM}=\cfrac{1}{2} \, \overrightarrow{AB} \rightarrow (x_3-x_1, y_3-y_1)=\cfrac{1}{2} \, (x_2-x_1, y_2-y_1) \rightarrow </math> | + | ::<math>\overrightarrow{AM}=\cfrac{1}{2} \, \overrightarrow{AB} \rightarrow (x_3-x_1, y_3-y_1)=\cfrac{1}{2} \, (x_2-x_1, y_2-y_1) \rightarrow </math> |
| - | :<math>\rightarrow | + | ::<math>\rightarrow |
| \begin{cases} | \begin{cases} | ||
| x_3-x_1=\cfrac{1}{2} \, (x_2-x_1) \rightarrow 2(x_3-x_1)=x_2-x_1 \rightarrow x_3=\cfrac{x_1+x_2}{2} | x_3-x_1=\cfrac{1}{2} \, (x_2-x_1) \rightarrow 2(x_3-x_1)=x_2-x_1 \rightarrow x_3=\cfrac{x_1+x_2}{2} | ||
| Línea 73: | Línea 74: | ||
| - | Con lo que obtenemos lo que buscabamos. | + | :Con lo que obtenemos lo que buscabamos. |
| }} | }} | ||
Revisión de 08:08 17 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sistema de referencia en el plano
Un sistema de referencia del plano consiste en una terna 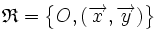 , donde
, donde  es un punto fijo, llamado origen, y
es un punto fijo, llamado origen, y 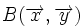 una base de vectores del plano.
una base de vectores del plano.
Vector de posición de un punto
- En un sistema de referencia
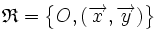 , cada punto
, cada punto  del plano tiene asociado un vector fijo
del plano tiene asociado un vector fijo 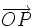 , llamado vector de posición del punto
, llamado vector de posición del punto  .
.
- Si el vector
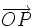 tiene coordenadas
tiene coordenadas 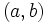 respecto de la base
respecto de la base 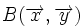 , el punto
, el punto  tendrá coordenadas
tendrá coordenadas 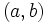 respecto del sistema de referencia
respecto del sistema de referencia 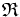 .
.
Vector de dirección de una recta
- Una recta queda determinada por un punto y un vector que fije su dirección, a dicho vector lo llamaremos vector de dirección de la recta.
- Dos puntos
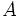 y
y 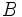 de una recta determinan un vector de dirección de la misma,
de una recta determinan un vector de dirección de la misma, 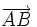 .
.
Coordenadas del vector que une dos puntos
Coordenadas del vector que une dos puntos
- Dados dos puntos del plano de coordenadas
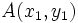 y
y 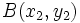 , respecto de un sistema de referencia
, respecto de un sistema de referencia 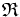 , entonces:
, entonces:
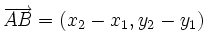
Demostración:
Como 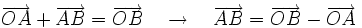
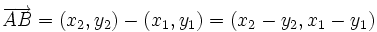
Condición para que tres puntos estén alineados
Condición para que tres puntos estén alineados
- Los puntos del plano
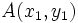 ,
, 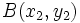 y
y 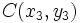 , están alineados si se cumple:
, están alineados si se cumple:
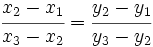
Demostración:
Los puntos del plano 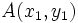 ,
, 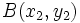 y
y 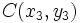 , están alineados si los vectores
, están alineados si los vectores 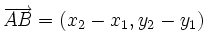 y
y 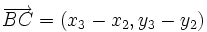 tienen la misma dirección.
tienen la misma dirección.
Ahora, esto ocurre si los vectores son proporcionales: 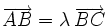
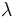 , se obtiene lo que buscamos.
, se obtiene lo que buscamos.Punto medio de un segmento
Punto medio de un segmento
- Las coordenadas del puinto medio,
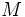 , de un segmento de extremos
, de un segmento de extremos 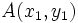 y
y 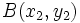 son:
son:
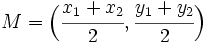
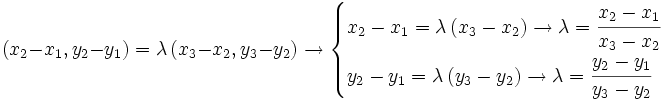
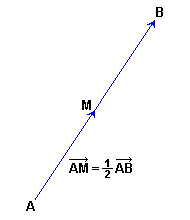
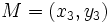 el punto medio del segmento
el punto medio del segmento