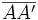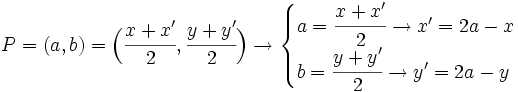Puntos y vectores el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:42 17 mar 2009 Coordinador (Discusión | contribuciones) (→Sistema de referencia en el plano) ← Ir a diferencia anterior |
Revisión de 10:27 17 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| <center><math>\overrightarrow{AB}=(x_2-x_1,y_2-y_1)</math></center> | <center><math>\overrightarrow{AB}=(x_2-x_1,y_2-y_1)</math></center> | ||
| |demo= | |demo= | ||
| - | Como {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB} \quad \rightarrow \quad \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}</math>}} | + | Partimos de que |
| - | Por tanto, {{sube|porcentaje=+35%|contenido=<math>\overrightarrow{AB}=(x_2,y_2)-(x_1,y_1)=(x_2-y_2,x_1-y_1)</math>}} | + | :{{sube|porcentaje=+30%|contenido=<math>\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB} \quad \rightarrow \quad \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}</math>}} |
| + | |||
| + | Por tanto, | ||
| + | |||
| + | :{{sube|porcentaje=+35%|contenido=<math>\overrightarrow{AB}=(x_2,y_2)-(x_1,y_1)=(x_2-y_2,x_1-y_1)</math>}} | ||
| }} | }} | ||
| }} | }} | ||
| Línea 63: | Línea 67: | ||
| <center><math>M=\Big( \cfrac{x_1+x_2}{2}, \cfrac{y_1+y_2}{2} \Big)</math></center> | <center><math>M=\Big( \cfrac{x_1+x_2}{2}, \cfrac{y_1+y_2}{2} \Big)</math></center> | ||
| |demo= | |demo= | ||
| - | :Sea <math>M=(x_3,y_3)\,</math> el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AB}</math>}}. Tenemos que: | + | Sea <math>M=(x_3,y_3)\,</math> el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AB}</math>}}. Tenemos que: |
| {{p}} | {{p}} | ||
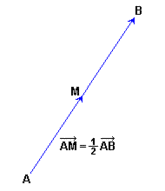
| - | ::<math>\overrightarrow{AM}=\cfrac{1}{2} \, \overrightarrow{AB} \rightarrow (x_3-x_1, y_3-y_1)=\cfrac{1}{2} \, (x_2-x_1, y_2-y_1) \rightarrow </math> | + | :<math>\overrightarrow{AM}=\cfrac{1}{2} \, \overrightarrow{AB} \rightarrow (x_3-x_1, y_3-y_1)=\cfrac{1}{2} \, (x_2-x_1, y_2-y_1) \rightarrow </math> |
| - | ::<math>\rightarrow | + | :<math>\rightarrow |
| \begin{cases} | \begin{cases} | ||
| x_3-x_1=\cfrac{1}{2} \, (x_2-x_1) \rightarrow 2(x_3-x_1)=x_2-x_1 \rightarrow x_3=\cfrac{x_1+x_2}{2} | x_3-x_1=\cfrac{1}{2} \, (x_2-x_1) \rightarrow 2(x_3-x_1)=x_2-x_1 \rightarrow x_3=\cfrac{x_1+x_2}{2} | ||
| Línea 76: | Línea 80: | ||
| - | :Con lo que obtenemos lo que buscabamos. | + | Con lo que obtenemos lo que buscabamos. |
| }} | }} | ||
| Línea 92: | Línea 96: | ||
| <center><math>A'=(2a-x,2b-y)\,</math>.</center> | <center><math>A'=(2a-x,2b-y)\,</math>.</center> | ||
| |demo= | |demo= | ||
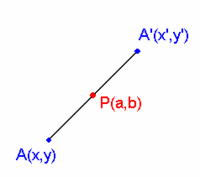
| - | :El punto <math>P(a,b)\,</math> es el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AA'}</math>}}. | + | El punto <math>P(a,b)\,</math> es el punto medio del segmento {{sube|porcentaje=+30%|contenido=<math>\overline{AA'}</math>}}. |
| - | :Aplicando la fórmula del punto medio: | + | Aplicando la fórmula del punto medio: |
| - | ::<math>P=(a,b)=\Big( \cfrac{x+x'}{2}, \cfrac{y+y'}{2} \Big) \rightarrow | + | :<math>P=(a,b)=\Big( \cfrac{x+x'}{2}, \cfrac{y+y'}{2} \Big) \rightarrow |
| \begin{cases} | \begin{cases} | ||
| a=\cfrac{x+x'}{2} \rightarrow x'=2a-x | a=\cfrac{x+x'}{2} \rightarrow x'=2a-x | ||
| Línea 104: | Línea 108: | ||
| - | :Con lo que obtenemos lo que buscabamos. | + | Con lo que obtenemos lo que buscabamos. |
| }} | }} | ||
| }} | }} | ||
Revisión de 10:27 17 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sistema de referencia en el plano
Un sistema de referencia del plano consiste en una terna 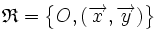 , donde
, donde  es un punto fijo, llamado origen, y
es un punto fijo, llamado origen, y 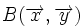 una base de vectores del plano.
una base de vectores del plano.
En este sistema de referencia, cada punto  del plano tiene asociado un vector fijo
del plano tiene asociado un vector fijo 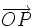 , llamado vector de posición del punto
, llamado vector de posición del punto  .
.
Si el vector 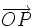 tiene coordenadas
tiene coordenadas 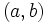 respecto de la base
respecto de la base 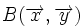 , el punto
, el punto  diremos que tiene coordenadas
diremos que tiene coordenadas 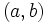 respecto del sistema de referencia
respecto del sistema de referencia 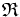 .
.
Normalmente trabajaremos con un sistema de referencia en el que la base es ortonormal.
Coordenadas del vector que une dos puntos
Condición para que tres puntos estén alineados
Condición para que tres puntos estén alineados
- Los puntos del plano
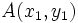 ,
, 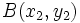 y
y 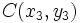 , están alineados si se cumple:
, están alineados si se cumple:
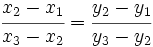
Demostración:
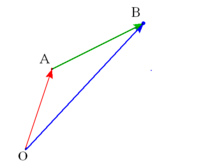
Los puntos del plano 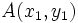 ,
, 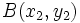 y
y 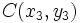 , están alineados si los vectores
, están alineados si los vectores 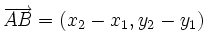 y
y 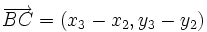 tienen la misma dirección.
tienen la misma dirección.
Ahora, esto ocurre si los vectores son proporcionales: 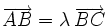
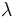 , se obtiene lo que buscamos.
, se obtiene lo que buscamos.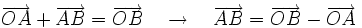
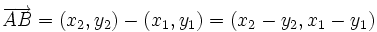
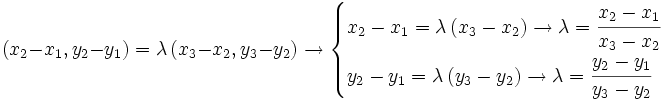
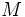 , de un segmento de extremos
, de un segmento de extremos 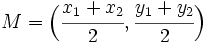
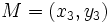 el punto medio del segmento
el punto medio del segmento 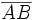
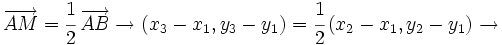
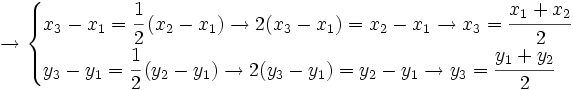
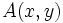 respecto del punto
respecto del punto 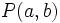 es:
es:
 .
.