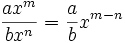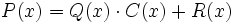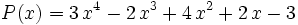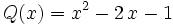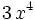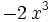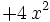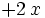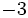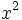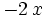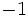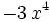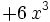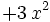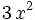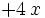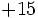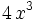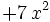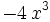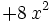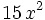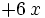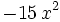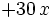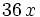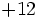Regla de Ruffini (4ºESO Académicas)
De Wikipedia
| Revisión de 13:55 9 jul 2008 Juanmf (Discusión | contribuciones) (→Cociente de monomios) ← Ir a diferencia anterior |
Revisión de 14:07 9 jul 2008 Juanmf (Discusión | contribuciones) (→Cociente de monomios) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===División de polinomios=== | ||
| + | La división de polinomios tiene la mismas partes que la [[división]] aritmética, así hay dos polinomios P(x) (dividendo) y Q(x) (divisor) de modo que el grado de P(x) sea mayor que el grado de Q(x) y el grado de Q(x) sea mayor o igual a cero, siempre hallaremos dos polinomios C(x) (cociente) y R(x) (resto) que podemos representar: | ||
| + | :{| | ||
| + | |- | ||
| + | | <math> P(x) \,</math> | ||
| + | | | ||
| + | | style="border-bottom:1px solid black; border-left:1px solid black; height:14px" | | ||
| + | <math> Q(x) \,</math> | ||
| + | |- | ||
| + | |align="center"| <math> R(x) \,</math> | ||
| + | | | ||
| + | |<math> C(x) \,</math> | ||
| + | |} | ||
| + | |||
| + | tal que: | ||
| + | : <math> P(x) = Q(x) \cdot C(x)+ R(x) \,</math> | ||
| + | : [[dividendo]] = [[divisor]] × [[cociente]] + [[resto]] | ||
| + | |||
| + | El grado de C(x) está determinado por la diferencia entre los grados de P(x) y Q(x), mientras que el grado de R(x) será, como máximo, un grado menor que Q(x). | ||
| + | |||
| + | * ejemplo: | ||
| + | veamos un ejemplo para: | ||
| + | : <math> P(x) = 3 \, x^{4} - 2 \, x^{3} + 4 \, x^{2} + 2 \, x - 3\;</math> | ||
| + | : <math> Q(x) = x^{2} - 2 \, x - 1 \;</math> | ||
| + | |||
| + | que para la realización de la división representamos: | ||
| + | :{| | ||
| + | |- align="right" | ||
| + | | <math> 3 \, x^{4} \;</math> | ||
| + | | <math> - 2 \, x^{3} \;</math> | ||
| + | | <math> + 4 \, x^{2} \;</math> | ||
| + | | <math> + 2 \, x \;</math> | ||
| + | | <math> - 3 \;</math> | ||
| + | | | ||
| + | | style="width:10px" | | ||
| + | | style="border-bottom:1px solid black; border-left:1px solid black" | | ||
| + | <math> x^{2} \;</math> | ||
| + | | style="border-bottom:1px solid black" | | ||
| + | <math> - 2 \, x \;</math> | ||
| + | | style="border-bottom:1px solid black" | | ||
| + | <math> - 1 \;</math> | ||
| + | |} | ||
| + | |||
| + | como resultado de la división finalizada: | ||
| + | :{| style="width:400px" | ||
| + | |- align="right" | ||
| + | | <math> 3 \, x^{4} \;</math> | ||
| + | | <math> - 2 \, x^{3} \;</math> | ||
| + | | <math> + 4 \, x^{2} \;</math> | ||
| + | | <math> + 2 \, x \;</math> | ||
| + | | <math> - 3 \;</math> | ||
| + | | | ||
| + | | style="width:10px" | | ||
| + | | style="border-bottom:1px solid black; border-left:1px solid black" | | ||
| + | <math> x^{2} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> - 2 \, x \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> - 1 \;</math> | ||
| + | |- align="right" | ||
| + | | style="border-bottom:1px solid black" | <math> - 3 \, x^{4} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 6 \, x^{3} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 3 \, x^{2} \;</math> | ||
| + | | style="border-bottom:1px solid black" | | ||
| + | | style="border-bottom:1px solid black" | | ||
| + | | | ||
| + | | | ||
| + | | <math> 3 \, x^{2} \;</math> | ||
| + | | <math> + 4 \, x \;</math> | ||
| + | | <math> + 15 \;</math> | ||
| + | |- align="right" | ||
| + | | | ||
| + | | <math> 4 \, x^{3} \; </math> | ||
| + | | <math> + 7 \, x^{2} \; </math> | ||
| + | | <math> + 2 \, x \;</math> | ||
| + | | <math> - 3 \;</math> | ||
| + | |- align="right" | ||
| + | | | ||
| + | | style="border-bottom:1px solid black" | <math> - 4 \, x^{3} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 8 \, x^{2} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 4 \, x \; </math> | ||
| + | | style="border-bottom:1px solid black" | | ||
| + | |- align="right" | ||
| + | | | ||
| + | | | ||
| + | | <math> 15 \, x^{2} \;</math> | ||
| + | | <math> + 6 \, x \;</math> | ||
| + | | <math> - 3 \;</math> | ||
| + | |- align="right" | ||
| + | | | ||
| + | | | ||
| + | | style="border-bottom:1px solid black" | <math> - 15 \, x^{2} \;</math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 30 \, x \; </math> | ||
| + | | style="border-bottom:1px solid black" | <math> + 15 \;</math> | ||
| + | |- align="right" | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | <math> 36 \, x \; </math> | ||
| + | | <math> + 12 \; </math> | ||
| + | |} | ||
| + | |||
| + | Cuando el resto sea igual a cero diremos que el dividendo es '''divisible''' por el divisor, es decir, que la división es exacta. | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 14:07 9 jul 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Cociente de monomios
Entenderemos la división como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
|
|
Ejemplos: División de monomios
- Calcula:
- a)
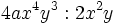
- b)
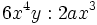
- a)
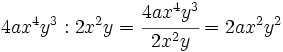
- b)
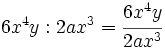 . No es posible la división pues no hay
. No es posible la división pues no hay  en el numerador.
en el numerador.
División de polinomios
La división de polinomios tiene la mismas partes que la división aritmética, así hay dos polinomios P(x) (dividendo) y Q(x) (divisor) de modo que el grado de P(x) sea mayor que el grado de Q(x) y el grado de Q(x) sea mayor o igual a cero, siempre hallaremos dos polinomios C(x) (cociente) y R(x) (resto) que podemos representar:
tal que:
El grado de C(x) está determinado por la diferencia entre los grados de P(x) y Q(x), mientras que el grado de R(x) será, como máximo, un grado menor que Q(x).
- ejemplo:
veamos un ejemplo para:
que para la realización de la división representamos:
como resultado de la división finalizada:
Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.