Vectores: Producto escalar (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:26 15 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:38 15 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades del producto escalar=== | + | ==Propiedades del producto escalar== |
| + | ===Perpendicularidad y producto escalar=== | ||
| {{Teorema||titulo=Nulidad y perpendicularidad|enunciado= | {{Teorema||titulo=Nulidad y perpendicularidad|enunciado= | ||
| '''1. Nulidad:''' Si cualquiera de los dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} o {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, es {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{0}</math>}}, entonces {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u} \cdot \overrightarrow{v}=0</math>}}. | '''1. Nulidad:''' Si cualquiera de los dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} o {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, es {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{0}</math>}}, entonces {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u} \cdot \overrightarrow{v}=0</math>}}. | ||
| Línea 26: | Línea 27: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===Signo del producto escalar=== | ||
| {{Teorema||titulo=Signo del producto escalar|enunciado= | {{Teorema||titulo=Signo del producto escalar|enunciado= | ||
| El '''signo del producto escalar''' queda determinado por el ángulo que forman los vectores: | El '''signo del producto escalar''' queda determinado por el ángulo que forman los vectores: | ||
| Línea 34: | Línea 36: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema||titulo=Proyección de vectores|enunciado= | + | ===Operaciones con el producto escalar=== |
| - | + | ||
| - | |demo= | + | |
| - | }} | + | |
| - | {{p}} | + | |
| {{Teorema||titulo=Operaciones|enunciado= | {{Teorema||titulo=Operaciones|enunciado= | ||
| - | *'''Propiedad conmutativa:''' <math>\overrightarrow{u} \cdot \overrightarrow{v}=<math>\overrightarrow{v} \cdot \overrightarrow{u}</math>. | + | *'''Propiedad conmutativa:''' <math>\overrightarrow{u} \cdot \overrightarrow{v}=\overrightarrow{v} \cdot \overrightarrow{u}</math>. |
| *'''Propiedad asociativa:''' <math>\lambda (\overrightarrow{u} \cdot \overrightarrow{v})=(\lambda \overrightarrow{u}) \cdot \overrightarrow{v}= \overrightarrow{u} \cdot (\lambda \overrightarrow{v})</math>. | *'''Propiedad asociativa:''' <math>\lambda (\overrightarrow{u} \cdot \overrightarrow{v})=(\lambda \overrightarrow{u}) \cdot \overrightarrow{v}= \overrightarrow{u} \cdot (\lambda \overrightarrow{v})</math>. | ||
| *'''Propiedad distributiva:''' <math>\overrightarrow{u} \cdot (\overrightarrow{v} + \overrightarrow{w})=\overrightarrow{u} \cdot \overrightarrow{v} + \overrightarrow{u} \cdot \overrightarrow{w}</math>. | *'''Propiedad distributiva:''' <math>\overrightarrow{u} \cdot (\overrightarrow{v} + \overrightarrow{w})=\overrightarrow{u} \cdot \overrightarrow{v} + \overrightarrow{u} \cdot \overrightarrow{w}</math>. | ||
| Línea 48: | Línea 46: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===Proyección de vectores y producto escalar=== | ||
| + | {{Teorema||titulo=Proyección de vectores|enunciado=[[Imagen:proyeccion.png|right]] | ||
| + | *El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él. | ||
| + | <math>\overrightarrow{u} \cdot \overrightarrow{v}=|\overrightarrow{v}| \, proy_{\overrightarrow{v}}(\overrightarrow{u})=|\overrightarrow{u}| \, proy_{\overrightarrow{u}}(\overrightarrow{v})</math> | ||
| - | + | |demo= | |
| - | + | ||
| - | {{Teorema_sin_demo|titulo=Combinación lineal de vectores|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, se puede poner como combinación lineal de ellos: {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math>}}. | + | |
| - | *Esta combinación lineal es única, es decir, sólo existen dos números <math>a\,</math> y <math>b\,</math> para los que se cumple la igualdad anterior. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Estos resultados permiten dar la siguiente definición: | + | {{Teorema||titulo=Corolarios|enunciado= |
| - | {{p}} | + | 1. |
| - | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones. La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | + | 2. |
| + | |demo= | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | De esta manera, los resultados anteriores se pueden reenunciar de la siguiente manera: | ||
| - | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Teorema de la base|enunciado=Cualquier vector del plano se puede poner como combinación lineal de los vectores de una base, de forma única. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Caja_Amarilla|texto=Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una '''base ortogonal'''. Si además ambos tienen módulo 1, se dice que forman una '''base ortonormal''' | ||
| - | }} | ||
| - | {{p}} | ||
| - | ==Coordenadas de un vector respecto de una base== | ||
| - | {{Caja_Amarilla|texto=Dada una base del plano {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, cualquier vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} se puede poner como combinación lineal de los vectores de dicha base, de forma única: | ||
| - | <center><math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math></center> | ||
| - | *El par de números <math>(a,b)\,</math>, diremos que son las '''coordenadas''' del vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} y lo expresaremos {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}=(a,b)</math>}}, o bien, {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}(a,b)</math>}}. | ||
| - | *Las coordenadas de los vectores de la base son {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{x}(1,0)</math>}} e {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{y}(0,1)</math>}}, ya que <math>\overrightarrow{x}=1 \overrightarrow{x}+0 \overrightarrow{y}</math> y <math>\overrightarrow{y}=0 \overrightarrow{x}+1 \overrightarrow{y}</math>. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Coordenadas de un vector respecto de una base''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la escena siguiente vas a hallar las coordenadas de un vector respecto de una base ortogonal. | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | En esta escena tenemos la base ortogonal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} y el vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}}, que en principio tiene de coordenadas (2,3)\, respecto de dicha base, ya que {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}=2 \overrightarrow{x} + 3 \overrightarrow{y}</math>}}. | ||
| - | |||
| - | Cambiando los valores de '''a''' y '''b''' puedes ver las distintas coordenadas que va teniendo los distintos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}} y la combinación lineal de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}} que nos da {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}}, pues {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}=a \overrightarrow{x} + b \overrightarrow{y}</math>}}. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_1.html | ||
| - | width=450 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | '''Ejercicio:''' | ||
| - | Representa al menos los vectores de coordenadas: <math>(-2, -3)\,</math>, <math>(1, 1)\,</math> , <math>(1, -1)\,</math>, <math>(0.5, 2)\,</math>, <math>(-1, 2.5)\,</math>, respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' En la escena siguiente vas a hallar las coordenadas de un vector respecto de una base que no es ortogonal. | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_2.html | ||
| - | width=450 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Halla las coordenadas del vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{u},\overrightarrow{v})</math>}}: | ||
| - | |||
| - | #Hay que formar un paralelogramo con las prolongaciones de los vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} (Variando '''a''' y '''b'''), de tal forma que {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} sea una diagonal del mismo. Por tanto esta vez, te conviene prolongar {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} en el sentido opuesto y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} en su mismo sentido. | ||
| - | #A continuación tienes que trazar paralelas a {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} desde el extremo de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}}, '''A''', para completar el paralelogramo. | ||
| - | #Escribe en tu cuaderno {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} como combinación lineal de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}. | ||
| - | #Escribe las coordenadas de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{u},\overrightarrow{v})</math>}}. | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | ==Operaciones con coordenadas== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | Sean {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}=(x_1,y_1)</math>}} y {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{v}=(x_2,y_2)</math>}} dos vectores del plano: | ||
| - | *'''Suma de vectores:''' {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}+\overrightarrow{v}=(x_1+x_2,y_1+y_2)</math>}} | ||
| - | *'''Producto por un número k:''' {{sube|porcentaje=+25%|contenido=<math>k \overrightarrow{u}=(k \, x_1,k \, y_1)</math>}} | ||
| - | *'''Combinación lineal:''' {{sube|porcentaje=+25%|contenido=<math>a \overrightarrow{u}+b \overrightarrow{v}=(a \, x_1+ b \, x_2, a \, y_1+b \, y_2)</math>}} | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Operaciones con coordenadas''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Coordenadas de la suma de dos vectores. | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | Comprueba en la siguiente escena como se obtienen las coordenadas de la suma de dos vectores respecto de la base ortonormal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | ||
| - | |||
| - | <center><math>\overrightarrow{u}=(-2,3) \, \quad \overrightarrow{v}=(5,2) \quad \rightarrow \quad \overrightarrow{u}+\overrightarrow{v}=(-2+5,3+2)=(3,5)</math></center> | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_3.html | ||
| - | width=450 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_3.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | '''Ejercicio:''' | ||
| - | Cambia el valor de los controles o mueve con el ratón los extremos de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} para comprobar la suma para las siguientes coordenadas: {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=(-4,0)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(4,3)</math>}} | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' Coordenadas de la combinación lineal de dos vectores. | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | Comprueba en la siguiente escena como se obtienen las coordenadas de la combinación lineal de dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=(-2,2)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(-3,1)</math>}},respecto de la base ortonormal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | ||
| - | |||
| - | <center><math>1.5 \overrightarrow{u}+2 \overrightarrow{v}=1.5 \, (-2,2)+ 2 \, (-3,-1)=(-3,3)+(-6,2)=(-9,1)</math></center> | ||
| - | |||
| - | Este resultado lo puedes ver en la escena, si haces '''a=1.5''' y '''b=2''' | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_4.html | ||
| - | width=450 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_4.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | '''Ejercicio:''' | ||
| - | |||
| - | Calcula en tu cuaderno las coordenadas, respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, de los vectores: | ||
| - | |||
| - | '''a)''' {{sube|porcentaje=+30%|contenido=<math>-\overrightarrow{u}-\overrightarrow{v}</math>}} | ||
| - | '''b)''' {{sube|porcentaje=+30%|contenido=<math>2 \overrightarrow{u}-1.5 \overrightarrow{v}</math>}} | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 12:38 15 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Producto escalar de vectores
Se llama producto escalar de dos vectores 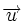 y
y 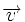 , al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
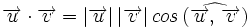
Propiedades del producto escalar
Perpendicularidad y producto escalar
Nulidad y perpendicularidad
1. Nulidad: Si cualquiera de los dos vectores, 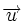 o
o 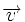 , es
, es 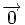 , entonces
, entonces 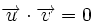 .
.
2. Perpendicularidad Dados dos vectores no nulos, 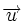 y
y 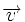 , se cumple que
, se cumple que
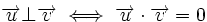
Demostración:
- Esta propiedad es inmediata.
- Si ambos vectores no son nulos, entonces, para que le productro escalar sea cero, debe ser cero el coseno del ángulo que forman esto ocurre sólo si el ángulo es de 90º.
Signo del producto escalar
Signo del producto escalar
El signo del producto escalar queda determinado por el ángulo que forman los vectores:
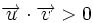 si
si 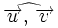 es agudo.
es agudo.
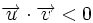 si
si 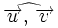 es obtuso.
es obtuso.
Demostración:
Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso.
Operaciones con el producto escalar
Operaciones
- Propiedad conmutativa:
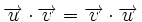 .
.
- Propiedad asociativa:
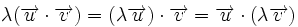 .
.
- Propiedad distributiva:
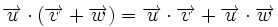 .
.
Demostración:
Proyección de vectores y producto escalar
Proyección de vectores
- El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él.
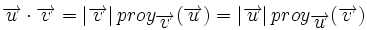
Demostración: