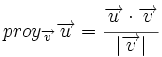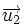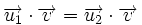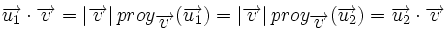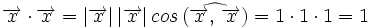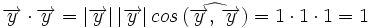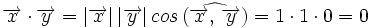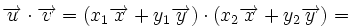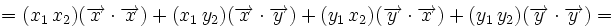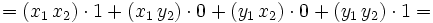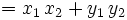Vectores: Producto escalar (1ºBach)
De Wikipedia
| Revisión de 08:13 16 mar 2009 Coordinador (Discusión | contribuciones) (→El producto escalar con bases ortonormales) ← Ir a diferencia anterior |
Revisión de 08:25 16 mar 2009 Coordinador (Discusión | contribuciones) (→El producto escalar con bases ortonormales) Ir a siguiente diferencia → |
||
| Línea 131: | Línea 131: | ||
| ===Módulo de un vector en una base ortonormal=== | ===Módulo de un vector en una base ortonormal=== | ||
| {{Teorema||titulo=Módulo de un vector|enunciado= | {{Teorema||titulo=Módulo de un vector|enunciado= | ||
| - | El módulo de un vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}(v_1,v_2)</math>}} respecto de una base otonormal {{sube|porcentaje=+15%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} es | + | El módulo de un vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}(v_1,v_2)</math>}}, respecto de una base otonormal, es |
| {{p}} | {{p}} | ||
| <center><math>|\overrightarrow{v}|=\sqrt{v_1^2+v_2^2}</math></center> | <center><math>|\overrightarrow{v}|=\sqrt{v_1^2+v_2^2}</math></center> | ||
| - | |demo=Si {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}(v_1,v_2)</math>}} respecto de una base otonormal, entonces: | + | |demo=Si {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(v_1,v_2)</math>}} respecto de una base otonormal, entonces: |
| <center><math>\overrightarrow{v} \cdot \overrightarrow{v}=v_1 \, v_1 + v_2 \, v_2=v_1^2+v_2^2</math></center> | <center><math>\overrightarrow{v} \cdot \overrightarrow{v}=v_1 \, v_1 + v_2 \, v_2=v_1^2+v_2^2</math></center> | ||
| Línea 146: | Línea 146: | ||
| Igualando ambos resultados tenemos lo que buscamos. | Igualando ambos resultados tenemos lo que buscamos. | ||
| }} | }} | ||
| + | {{p}} | ||
| ===Ángulo de dos vectores en una base ortonormal=== | ===Ángulo de dos vectores en una base ortonormal=== | ||
| + | {{Teorema||titulo=Ángulo entre dos vectores|enunciado= | ||
| + | Dados dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}(u_1,u_2)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}(v_1,v_2)</math>}}, respecto de una base otonormal, se cumple que | ||
| + | {{p}} | ||
| + | <center><math>cos \, (\widehat{\overrightarrow{u}, \, \overrightarrow{v}})=\cfrac{u_1 \, v_1 + u_2 \, v_2}{\sqrt{u_1^2+u_2^2} \, \sqrt{v_1^2+v_2^2}}</math></center> | ||
| + | |||
| + | |demo=Si {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=(u_1,u_2)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(v_1,v_2)</math>}}, respecto de una base otonormal, entonces: | ||
| + | |||
| + | <center><math>\overrightarrow{u} \cdot \overrightarrow{v}=u_1 \, v_1 + u_2 \, v_2 \qquad |\overrightarrow{u}|=\sqrt{u_1^2+u_2^2} \qquad |\overrightarrow{v}|=\sqrt{v_1^2+v_2^2}</math></center> | ||
| + | |||
| + | Por otro lado: | ||
| + | |||
| + | <center><math>\overrightarrow{u} \cdot \overrightarrow{v}=|\overrightarrow{u}| \, |\overrightarrow{v}| \, cos \, (\widehat{\overrightarrow{u}, \, \overrightarrow{v}}) \quad \rightarrow \quad cos \, (\widehat{\overrightarrow{u}, \, \overrightarrow{v}})=\cfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{|\overrightarrow{u}| \, |\overrightarrow{v}|}</math></center> | ||
| + | |||
| + | Sustituyendo en esta última expresión las anteriores, tenemos lo que buscamos. | ||
| + | }} | ||
| + | {{p}} | ||
| ===Vector ortogonal a otro=== | ===Vector ortogonal a otro=== | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 08:25 16 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Act. Interactivas | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Producto escalar de vectores
Se llama producto escalar de dos vectores 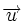 y
y 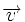 , al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
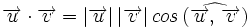
Propiedades del producto escalar
Propiedad fundamental del producto escalar
Propiedad fundamental
- Si cualquiera de los dos vectores,
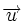 o
o 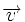 , es
, es 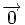 , entonces
, entonces 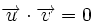 .
.
- Dados dos vectores no nulos,
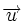 y
y 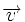 , se cumple que
, se cumple que
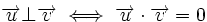
- La primera propiedad es inmediata.
- Para la segunda propiedad, si ambos vectores no son nulos, entonces, para que el producto escalar sea cero, debe ser cero el coseno del ángulo que forman, y esto ocurre sólo si el ángulo es de 90º.
Signo del producto escalar
Propiedades: signo del producto escalar
El signo del producto escalar queda determinado por el ángulo que forman los vectores:
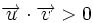 si
si 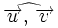 es agudo.
es agudo.
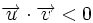 si
si 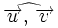 es obtuso.
es obtuso.
Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso.
Operaciones con el producto escalar
Propiedades de las operaciones
- Propiedad conmutativa:
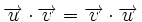 .
.
- Propiedad asociativa:
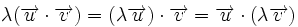 .
.
- Propiedad distributiva:
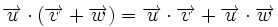 .
.
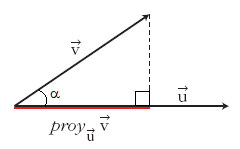
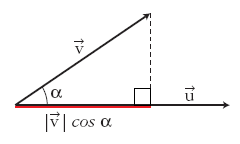
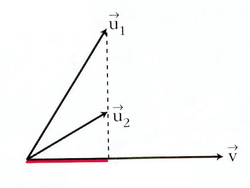
Proyección de vectores y producto escalar
Llamaremos proyección del vector 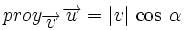 siendo Observa que la proyección es un número positivo o negativo según lo sea |
El producto escalar con bases ortonormales
Expresión analítica del producto escalar en bases ortonormales
Proposición
Sea 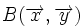 una base ortonormal, entonces
una base ortonormal, entonces
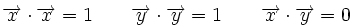
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
Proposición
Si las coordenadas de los vectores 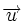 y
y 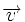 , respecto de una base otonormal
, respecto de una base otonormal 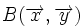 son
son 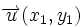 y
y 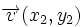 , entonces:
, entonces:
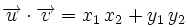
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
Módulo de un vector en una base ortonormal
Módulo de un vector
El módulo de un vector 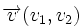 , respecto de una base otonormal, es
, respecto de una base otonormal, es
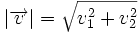
Si 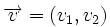 respecto de una base otonormal, entonces:
respecto de una base otonormal, entonces:
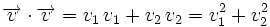
Por otro lado:
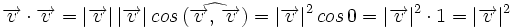
Ángulo de dos vectores en una base ortonormal
Ángulo entre dos vectores
Dados dos vectores, 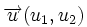 y
y 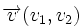 , respecto de una base otonormal, se cumple que
, respecto de una base otonormal, se cumple que
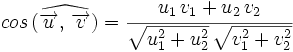
Si 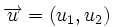 y
y 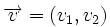 , respecto de una base otonormal, entonces:
, respecto de una base otonormal, entonces:
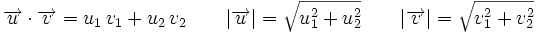
Por otro lado:
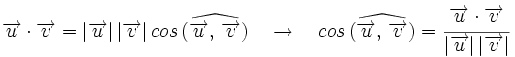
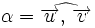
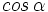 .
.
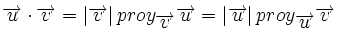
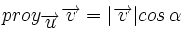
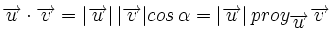
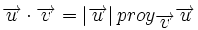 </center>
</center>