Vectores: Producto escalar (1ºBach)
De Wikipedia
| Revisión de 12:21 15 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) |
||
| Línea 2: | Línea 2: | ||
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| - | |repasar= | + | |repasar=[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Vectores_en_el_plano/Vectores6.htm#11producto Act. Interactivas] |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| ==Producto escalar de vectores== | ==Producto escalar de vectores== | ||
| - | '''Texto en negrita'''{{Caja_Amarilla|texto=Se llama '''producto escalar''' de dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman: | + | {{Caja_Amarilla|texto=Se llama '''producto escalar''' de dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman: |
| - | <center><math>\overrightarrow{u} \cdot \overrightarrow{v}=|\overrightarrow{u}| \, |\overrightarrow{v}| \, cos \, (\widehat{\overrightarrow{u}, \, \overrightarrow{v}})</math></center> | + | <center><math>\vec{u} \cdot \vec{v}=|\vec{u}| \, |\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})</math></center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades del producto escalar=== | + | {{Nota|titulo=Nota:|texto=Como dos vectores forman dos ángulos entre sí, tomaremos el menor de ellos. De todas formas, para el cálculo del producto escalar da igual que tomemos uno u otro, ya que ambos ángulos son opuestos y, por tanto, tienen el mismo coseno.}} |
| - | {{Teorema||titulo=Nulidad y perpendicularidad|enunciado= | + | {{p}} |
| - | '''1. Nulidad:''' Si cualquiera de los dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} o {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, es {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{0}</math>}}, entonces {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u} \cdot \overrightarrow{v}=0</math>}}. | + | {{Video_enlace |
| + | |titulo1=Producto escalar de dos vectores | ||
| + | |duracion=19´54" | ||
| + | |url1=https://youtu.be/ZpnRfRPGd1Y | ||
| + | |sinopsis=Vídeo que condensa los resultados más importantes que se van a desarrollar a lo largo de esta página sobre el producto escalar de dos vectores en el plano. | ||
| + | }} | ||
| - | '''2. Perpendicularidad''' Dados dos vectores no nulos, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, se cumple que | + | ==Propiedades del producto escalar== |
| + | ===Propiedad fundamental del producto escalar=== | ||
| + | {{Teorema||titulo=Propiedades (1)|enunciado= | ||
| + | *Si {{sube|porcentaje=+30%|contenido=<math>\vec{u}=\vec{0}</math>}} ó {{sube|porcentaje=+30%|contenido=<math>\vec{v}=\vec{0}</math>}} entonces {{sube|porcentaje=+30%|contenido=<math>\vec{u} \cdot \vec{v}=0</math>}}. | ||
| - | <center><math>\overrightarrow{u} \bot \overrightarrow{v} \iff \overrightarrow{u} \cdot \overrightarrow{v}=0</math></center> | + | * {{sube|porcentaje=+30%|contenido=<math>\forall \, \vec{u} \, , \vec{v} \ne \vec{0}</math>}} se cumple que {{sube|porcentaje=+30%|contenido=<math>\vec{u} \bot \vec{v} \iff \vec{u} \cdot \vec{v}=0</math>}} |
| |demo= | |demo= | ||
| - | #Esta propiedad es inmediata. | + | *La primera propiedad es inmediata. |
| - | #Si ambos vectores no son nulos, entonces, para que le productro escalar sea cero, debe ser cero el coseno del ángulo que forman esto ocurre sólo si el ángulo es de 90º. | + | *Para la segunda propiedad, si ambos vectores no son nulos, entonces, el producto escalar es cero si y solo si el coseno del ángulo que forman es cero, y esto ocurre si sólo si el ángulo es de 90º ó -90º. |
| - | # | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema||titulo=Signo del producto escalar|enunciado= | + | {{Video_enlace_matefacil |
| - | El signo del producto escalar queda determinado por el ángulo que forman los vectores: | + | |titulo1=Vectores ortogonales |
| - | :*<math>\overrightarrow{u} \cdot \overrightarrow{v}>0</math> si <math>\widehat{\overrightarrow{u}, \, \overrightarrow{v}}</math> es agudo. | + | |duracion=7´44" |
| - | :*<math>\overrightarrow{u} \cdot \overrightarrow{v}<0</math> si <math>\widehat{\overrightarrow{u}, \, \overrightarrow{v}}</math> es obtuso. | + | |url1=https://www.youtube.com/watch?v=wZT76JBC64A&index=35&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A |
| + | |sinopsis= | ||
| + | *Dos vectores son perpendiculares si y sólo si su producto escalar es cero | ||
| + | *Ejemplos. | ||
| + | {{p}} | ||
| + | Nota: A lo largo del video también se ven ejemplos con vectores tridimensionales. | ||
| + | }} | ||
| + | |||
| + | ===Signo del producto escalar=== | ||
| + | {{Teorema||titulo=Propiedades (2)|enunciado= | ||
| + | El '''signo del producto escalar''' queda determinado por el ángulo que forman los vectores: | ||
| + | *<math>\vec{u} \cdot \vec{v}>0</math> si <math>\widehat{\vec{u}, \, \vec{v}}</math> es agudo. | ||
| + | *<math>\vec{u} \cdot \vec{v}<0</math> si <math>\widehat{\vec{u}, \, \vec{v}}</math> es obtuso. | ||
| |demo= | |demo= | ||
| Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso. | Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema||titulo=Proyección de vectores|enunciado= | + | {{Geogebra_enlace |
| + | |descripcion=En esta escena podrás ver como se calcula el producto escalar de vectores y cómo es su signo. | ||
| + | |enlace=[https://ggbm.at/AutHpxv5 Signo del producto escalar de vectores] | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Propiedades del producto escalar=== | ||
| + | {{Teorema||titulo=Propiedades (3)|enunciado= | ||
| + | *'''Conmutativa:''' <math>\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{u}</math> | ||
| + | |||
| + | *'''Asociativa mixta:''' <math>\lambda (\vec{u} \cdot \vec{v})=(\lambda \vec{u}) \cdot \vec{v}= \vec{u} \cdot (\lambda \vec{v})\, , \quad \forall \lambda \in \mathbb{R}</math> | ||
| + | |||
| + | *'''Distributiva:''' <math>\vec{u} \cdot (\vec{v} + \vec{w})=\vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}</math> | ||
| + | |||
| + | *<math>\vec{v} \cdot \vec{v} = |\vec{v}|^2</math> | ||
| |demo= | |demo= | ||
| + | *'''Propiedad conmutativa:''' | ||
| + | :<math>\vec{u} \cdot \vec{v}=|\vec{u}| \, |\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})\begin{matrix} ~_{(1)}~ \\ = \\ ~ \end{matrix} |\vec{v}| \, |\vec{u}| \, cos \, (v,u)=\vec{v} \cdot \vec{u}</math> | ||
| + | |||
| + | <math>(1): \, cos \, \alpha=cos \, (-\alpha) \rightarrow cos \, (\widehat{\vec{u}, \, \vec{v}})=cos \, (\widehat{\vec{v}, \, \vec{u}})</math> | ||
| + | |||
| + | |||
| + | *'''Propiedad asociativa:''' | ||
| + | :<math>\lambda (\vec{u} \cdot \vec{v})=\lambda \, |\vec{u}| \, |\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})</math> | ||
| + | :<math>(\lambda \vec{u}) \cdot \vec{v}=|\lambda \, \vec{u}| \, |\vec{v}| \, cos \, (\widehat{\lambda \, \vec{u}, \, \vec{v}}) \begin{matrix} ~_{(2)}~ \\ = \\ ~ \end{matrix}|\lambda | \, |\vec{u}| \, |\vec{v}| \cdot \, signo(\lambda) \cdot cos \, (\widehat{\vec{u}, \, \vec{v}})=</math> | ||
| + | :<math>=\lambda \, |\vec{u}| \, |\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})</math> | ||
| + | |||
| + | <math>(2): \, cos \, (\widehat{\lambda \, \vec{u}, \, \vec{v}})=signo(\lambda) \cdot cos \, (\widehat{ \vec{u}, \, \vec{v}})</math>, ya que el ángulo es igual si <math>\lambda>0\,</math> y suplementario si <math>\lambda<0\,</math>.{{p}} | ||
| + | :(Recuerda que ángulos suplementarios tienen cosenos opuestos). | ||
| + | |||
| + | :Así tenemos una de las igualdades: <math>\lambda (\vec{u} \cdot \vec{v})=(\lambda \vec{u}) \cdot \vec{v}</math>. La otra igualdad se obtendría de forma similar. | ||
| + | |||
| + | |||
| + | *'''Propiedad distributiva:''' [[Imagen:distributivaescalar.png|right|250px]] | ||
| + | :<math>\vec{u} \cdot (\vec{v} + \vec{w})=|\vec{u}| |\vec{v} + \vec{u}| \, cos \, (\widehat{\vec{u}, \, \vec{v}+\vec{w}})=|\vec{u}| \cdot proy_\vec{u}(\vec{v}+\vec{w})</math> | ||
| + | :<math>\vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}=|\vec{u}||\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})+|\vec{u}||\vec{w}| \, cos \, (\widehat{\vec{u}, \, \vec{w}})=</math> | ||
| + | |||
| + | ::::::<math>=|\vec{u}|[|\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})+|\vec{w}| \, cos \, (\widehat{\vec{u}, \, \vec{w}})]=</math> | ||
| + | |||
| + | ::::::<math>=|\vec{u}| \cdot [proy_\vec{u} \vec{v}+proy_\vec{u} \vec{w}]=|\vec{u}| \cdot [proy_\vec{u} (\vec{v}+ \vec{w})]</math> | ||
| + | |||
| + | :Obteniendo la igualdad buscada. | ||
| + | |||
| + | *La última propiedad es fácil: | ||
| + | :<math>\vec{v} \cdot \vec{v}=|\vec{v}| \, |\vec{v}| \, cos \, (\widehat{\vec{v}, \, \vec{v}})=|\vec{v}|^2 \, cos \, 0^o=|\vec{v}|^2 \cdot 1=|\vec{v}|^2</math> | ||
| + | |||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema||titulo=Operaciones|enunciado= | ||
| - | *'''Propiedad conmutativa:''' <math>\overrightarrow{u} \cdot \overrightarrow{v}=<math>\overrightarrow{v} \cdot \overrightarrow{u}</math></math> | ||
| - | |demo=[http://maralboran.org/web_ma/Anaya/Anaya07/1BT_ALUMNO/Datos/Unidades/07/CDa_1bach_CC_t07_1_mec.pdf Ver demostración] | + | ===Proyección de vectores y producto escalar=== |
| + | {{Tabla75|celda2=<center>[[Imagen:proyeccion2.png]]<br>[[Imagen:proyeccion.png]]</center> | ||
| + | |celda1= | ||
| + | {{Caja_Amarilla|texto=Llamaremos '''proyección''' del vector {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}} sobre el vector {{sube|porcentaje=+30%|contenido=<math>\vec{u}</math>}}, al número | ||
| + | |||
| + | <center><math>proy_{\vec{u}}\, \vec{v}=|v| \, \cos \, \alpha \qquad</math></center> | ||
| + | |||
| + | siendo {{sube|porcentaje=+20%|contenido=<math>\alpha= \widehat{\vec{u}, \, \vec{v}}</math>}} el ángulo que forman los dos vectores. | ||
| + | Observa que la proyección es un número positivo o negativo según lo sea <math>cos \, \alpha</math>. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
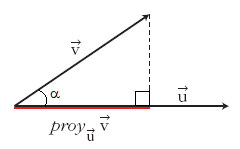
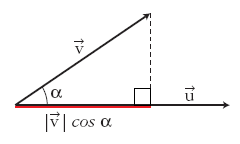
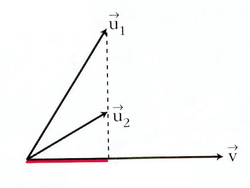
| + | Gráficamente es como la sombra (ver segmento rojo en figura adjunta) que proyecta <math>\vec{v}</math> perpendicularmente sobre <math>\vec{u}</math>, si pusieramos una luz encima de ellos. | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Nota:|texto=Aquí la proyección se define como un escalar (la medida del segmento rojo de la figura de la derecha). Otras veces, la proyección se define como el vector que determina la sombra tomando como origen, el origen común de los dos vectores, y como extremo, el de la intersección con la línea discontinua perpendicular al vector <math>\vec{u}</math> (ver figura adjunta). En tal caso, para obtener el vector proyección, deberíamos multiplicar el valor de la proyección (escalar) por el vector <math>\vec{u}</math> hecho unitario: | ||
| + | <center><math>\vec{proy}_{\vec{u}}\, \vec{v}=proy_{\vec{u}}\, \vec{v} \cdot \cfrac{\vec{u}}{|\vec{u}|}</math></center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema||titulo=Proposición (4)|enunciado= | ||
| + | El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él. | ||
| + | {{p}} | ||
| + | <center><math>\vec{u} \cdot \vec{v} \, = \, |\vec{v}| \, proy_{\vec{v}}\, \vec{u} \, = \, |\vec{u}| \, proy_{\vec{u}}\, \vec{v}</math></center> | ||
| + | {{p}} | ||
| + | En consecuencia: | ||
| + | {{p}} | ||
| + | <center><math>proy_{\vec{v}}\, \vec{u}=\cfrac{\vec{u} \cdot \vec{v}}{|\vec{v}|} \qquad proy_{\vec{u}}\, \vec{v}=\cfrac{\vec{u} \cdot \vec{v}}{|\vec{u}|}</math></center> | ||
| + | |demo= | ||
| + | Si observamos el dibujo de la derecha, tenemos que | ||
| + | {{p}} | ||
| + | <center><math>proy_{\vec{u}}\, \vec{v}=|\vec{v}|cos \, \alpha</math></center> | ||
| + | {{p}} | ||
| + | Entonces | ||
| + | {{p}} | ||
| + | <center><math>\vec{u} \cdot \vec{v}=|\vec{u}| \, |\vec{v}| cos \, \alpha=|\vec{u}| \, proy_{\vec{u}}\, \vec{v}</math></center> | ||
| + | {{p}} | ||
| + | De la misma manera se obtiene la otra relación: | ||
| + | {{p}} | ||
| + | <math>\vec{u} \cdot \vec{v}=|\vec{u}| \, proy_{\vec{v}}\, \vec{u}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Nota:|texto=Si consideramos la proyección como vector, tendremos: | ||
| + | |||
| + | <center><math>\vec{proy}_{\vec{u}}\, \vec{v}=proy_{\vec{u}}\, \vec{v} \cdot \cfrac{\vec{u}}{|\vec{u}|}=\cfrac{\vec{u} \cdot \vec{v}}{|\vec{u}|}\cdot \cfrac{\vec{u}}{|\vec{u}|}=\cfrac{\vec{u} \cdot \vec{v}}{\vec{u} \cdot \vec{u}}\cdot \vec{u}</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Proyección de vectores y producto escalar | ||
| + | |duracion=13´54" | ||
| + | |url1=https://youtu.be/VSuveo_lgKE?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Proyección de vectores y producto escalar. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=6´25" | ||
| + | |url1=https://www.youtube.com/watch?v=d4_6-kF1HdY | ||
| + | |sinopsis=Sean <math>\vec{v}=(3,1)</math> y <math>\vec{w}=(1,5)</math>. Halla el vector proyección <math>\vec{proy}_{\vec{v}}\, \vec{w}</math> y su módulo, es decir, <math>proy_{\vec{v}}\, \vec{w}</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Tabla75|celda2=<center>[[Imagen:proyeccion3.png|250px]]</center> | ||
| + | |celda1= | ||
| + | {{Teorema||titulo=Corolario (5): ''Proyecciones coincidentes''|enunciado= | ||
| + | Si las proyecciones sobre {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}} de {{sube|porcentaje=+30%|contenido=<math>\vec{u_1}</math>}} y de {{sube|porcentaje=+30%|contenido=<math>\vec{u_2}</math>}} coinciden, entonces: | ||
| + | {{p}} | ||
| + | <center><math>\vec{u_1} \cdot \vec{v}= \vec{u_2} \cdot \vec{v}</math></center> | ||
| + | |demo= | ||
| + | <math>\vec{u_1} \cdot \vec{v}=|\vec{v}| \, proy_{\vec{v}} \, (\vec{u_1})=|\vec{v}| \, proy_{\vec{v}}\, (\vec{u_2})=\vec{u_2} \cdot \vec{v}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver como se representa y calcula la proyección de un vector sobre otro. | ||
| + | |enlace=[https://ggbm.at/jrZA5bKp Proyecciones de vectores] | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Producto escalar'' | ||
| + | |cuerpo= | ||
| + | (Pág. 176) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 3, 4, 5 | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]] 1, 2 | ||
| - | {{Teorema_sin_demo|titulo=Combinación lineal de vectores|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, se puede poner como combinación lineal de ellos: {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math>}}. | ||
| - | *Esta combinación lineal es única, es decir, sólo existen dos números <math>a\,</math> y <math>b\,</math> para los que se cumple la igualdad anterior. | ||
| }} | }} | ||
| + | |||
| + | ==El producto escalar con bases ortonormales== | ||
| + | ===Expresión analítica del producto escalar en bases ortonormales=== | ||
| + | {{Teorema||titulo=Proposición (6)|enunciado= | ||
| + | Sea {{sube|porcentaje=+15%|contenido=<math>B(\vec{x},\vec{y})</math>}} una base ortonormal, entonces | ||
| {{p}} | {{p}} | ||
| - | Estos resultados permiten dar la siguiente definición: | + | <center><math>\vec{x} \cdot \vec{x}=1 \qquad \vec{y} \cdot \vec{y}=1 \qquad \vec{x} \cdot \vec{y}=0</math></center> |
| + | |||
| + | |demo=En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos: | ||
| + | |||
| + | :<math>\vec{x} \cdot \vec{x}=|\vec{x}| \, |\vec{x}| \, cos \, (\widehat{\vec{x}, \, \vec{x}})=1 \cdot 1 \cdot 1=1</math> | ||
| + | |||
| + | :<math>\vec{y} \cdot \vec{y}=|\vec{y}| \, |\vec{y}| \, cos \, (\widehat{\vec{y}, \, \vec{y}})=1 \cdot 1 \cdot 1=1</math> | ||
| + | |||
| + | :<math>\vec{x} \cdot \vec{y}=|\vec{x}| \, |\vec{y}| \, cos \, (\widehat{\vec{x}, \, \vec{y}})=1 \cdot 1 \cdot 0=0</math> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones. La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | + | {{Teorema||titulo=Proposición (7)|enunciado= |
| + | Si las coordenadas de los vectores {{sube|porcentaje=+30%|contenido=<math>\vec{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, respecto de una base otonormal {{sube|porcentaje=+15%|contenido=<math>B(\vec{x},\vec{y})</math>}} son {{sube|porcentaje=+10%|contenido=<math>\vec{u}(x_1,y_1)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}(x_2,y_2)</math>}}, entonces: | ||
| + | {{p}} | ||
| + | <center><math>\vec{u} \cdot \vec{v}=x_1 \, x_2 + y_1 \, y_2</math></center> | ||
| + | |||
| + | |demo=En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos: | ||
| + | |||
| + | :<math>\vec{u} \cdot \vec{v}=(x_1 \vec{x}+y_1 \vec{y}) \cdot (x_2 \vec{x}+y_2 \vec{y})=</math> | ||
| + | :::<math>=(x_1 \, x_2)(\vec{x} \cdot \vec{x})+(x_1 \, y_2)(\vec{x} \cdot \vec{y})+(y_1 \, x_2)(\vec{y} \cdot \vec{x})+(y_1 \, y_2)(\vec{y} \cdot \vec{y})=</math> | ||
| + | |||
| + | :::<math>=(x_1 \, x_2) \cdot 1+(x_1 \, y_2) \cdot 0+(y_1 \, x_2) \cdot 0+(y_1 \, y_2) \cdot 1=</math> | ||
| + | :::<math>=x_1 \, x_2 + y_1 \, y_2</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | De esta manera, los resultados anteriores se pueden reenunciar de la siguiente manera: | + | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Dados los vectores {{sube|porcentaje=+10%|contenido=<math>\vec{u}(2,-1)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}(3,2)</math>}}, respecto de una base otonormal, vamos a calcular {{sube|porcentaje=+20%|contenido=<math>\vec{u} \cdot \vec{v}</math>}}: |
| + | |||
| + | :<math>\vec{u} \cdot \vec{v}=(2,-1) \cdot (3,2)=2 \cdot 3 + (-1) \cdot 2=6-2=4</math> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Teorema de la base|enunciado=Cualquier vector del plano se puede poner como combinación lineal de los vectores de una base, de forma única. | + | {{Video_enlace_pablo |
| + | |titulo1=Base canónica. Producto escalar en la base canónica. | ||
| + | |duracion=12´16" | ||
| + | |url1=https://youtu.be/WpfLOZ2VuBo?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis= | ||
| + | *Base canónica. | ||
| + | *Cálculo del producto escalar de vectores del plano en la base canónica. | ||
| }} | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejemplo | ||
| + | |duracion=7´23" | ||
| + | |url1=https://www.youtube.com/watch?v=N5f7pYTNcFM&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A&index=31 | ||
| + | |sinopsis= | ||
| + | *Cálculo del producto escalar de vectores del plano. | ||
| + | *Ejemplos. | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una '''base ortogonal'''. Si además ambos tienen módulo 1, se dice que forman una '''base ortonormal''' | + | Nota: A lo largo del video también se trata el caso de vectores tridimensionales. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Coordenadas de un vector respecto de una base== | + | {{Geogebra_enlace |
| - | {{Caja_Amarilla|texto=Dada una base del plano {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, cualquier vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} se puede poner como combinación lineal de los vectores de dicha base, de forma única: | + | |descripcion=En esta escena podrás ver como se representa el producto escalar de dos vectores. |
| + | |enlace=[https://ggbm.at/MWQuD4ez Producto escalar de vectores] | ||
| + | }} | ||
| - | <center><math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math></center> | + | {{p}} |
| + | {{wolfram desplegable|titulo=Producto escalar de vectores|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Producto escalar de vectores'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | a) Sean <math>\vec{u} =(3,5)</math> y <math>\vec{v} =(3,4)</math>. Halla el producto escalar <math>\vec{u}\cdot \vec{v}</math> | ||
| + | |||
| + | b) Averigua el valor de <math>x\;</math> para que los vectores <math>\vec{u} =(x,5)</math> y <math>\vec{v} =(2,3)</math> sean ortogonales. | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | :a) {{consulta|texto=(3,5)·(3,4)}} | ||
| + | |||
| + | :b) {{consulta|texto=solve (x,5)·(2,3)=0}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | |||
| + | }} | ||
| - | *El par de números <math>(a,b)\,</math>, diremos que son las '''coordenadas''' del vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} y lo expresaremos {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}=(a,b)</math>}}, o bien, {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}(a,b)</math>}}. | ||
| - | *Las coordenadas de los vectores de la base son {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{x}(1,0)</math>}} e {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{y}(0,1)</math>}}, ya que <math>\overrightarrow{x}=1 \overrightarrow{x}+0 \overrightarrow{y}</math> y <math>\overrightarrow{y}=0 \overrightarrow{x}+1 \overrightarrow{y}</math>. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Coordenadas de un vector respecto de una base''|cuerpo= | + | |
| - | {{ai_cuerpo | + | ===Vector ortogonal a otro=== |
| - | |enunciado='''Actividad 1:''' En la escena siguiente vas a hallar las coordenadas de un vector respecto de una base ortogonal. | + | {{Teorema||titulo=Proposición (8)|enunciado=Los vectores de coordenadas {{sube|porcentaje=+10%|contenido=<math>\vec{u}(a,b)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}(-b,a)</math>}}, respecto de una base ortonormal, son ortogonales. |
| + | |demo=Por la propiedad fundamental, sabemos que: | ||
| + | |||
| + | <center><math>\vec{u} \bot \vec{v} \iff \vec{u} \cdot \vec{v}=0</math></center> | ||
| + | |||
| + | Por otro lado, como las base es ortonormal, la expresión analítica del producto escalar es | ||
| + | |||
| + | <center><math>\vec{u} \cdot \vec{v}=a \cdot (-b) + b \cdot a=0</math></center> | ||
| + | |||
| + | De manera que el producto escalar vale cero y, por tanto, los vectores son ortogonales. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | |actividad= | + | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Halla 3 vectores ortogonales a (2,3). |
| - | En esta escena tenemos la base ortogonal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} y el vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}}, que en principio tiene de coordenadas (2,3)\, respecto de dicha base, ya que {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}=2 \overrightarrow{x} + 3 \overrightarrow{y}</math>}}. | + | ---- |
| + | '''Solución:''' | ||
| + | Por la proposición anterior: (-3,2). | ||
| - | Cambiando los valores de '''a''' y '''b''' puedes ver las distintas coordenadas que va teniendo los distintos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}} y la combinación lineal de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}} que nos da {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}</math>}}, pues {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{z}=a \overrightarrow{x} + b \overrightarrow{y}</math>}}. | + | Cualquier múltiplo de (-3,2) también será ortogonal: (3,-2) y (-6,4) |
| - | <center><iframe> | + | }} |
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_1.html | + | {{p}} |
| - | width=450 | + | {{Ejemplo|titulo=Ejemplo:|enunciado=Calcula el valor de <math>x\,</math> para que el vector {{sube|porcentaje=+10%|contenido=<math>\vec{u}(x,1)</math>}} sea ortogonal a {{sube|porcentaje=+10%|contenido=<math>\vec{v}(-2,5)</math>}}, respecto de una base ortonormal. |
| - | height=410 | + | |sol= |
| - | name=myframe | + | Al venir dadas las coordenadas respecto de una base ortonormal, para que los vectores dados sean ortogonales, su producto escalar debe ser cero: |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | '''Ejercicio:''' | + | :<math>(x,1) \cdot (-2,5)=0 \quad \rightarrow \quad -2x+5=0 \quad \rightarrow \quad x=\cfrac{5}{2}</math> |
| - | Representa al menos los vectores de coordenadas: <math>(-2, -3)\,</math>, <math>(1, 1)\,</math> , <math>(1, -1)\,</math>, <math>(0.5, 2)\,</math>, <math>(-1, 2.5)\,</math>, respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | + | }} |
| + | {{p}} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Producto escalar de vectores ortogonales | ||
| + | |duracion=4´54" | ||
| + | |url1=https://youtu.be/hTpIPlPLm14?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | |sinopsis=Producto escalar de vectores ortogonales. Obtención de un vector ortogonal a uno dado. Ejemplos. | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{Geogebra_enlace |
| - | |enunciado='''Actividad 2:''' En la escena siguiente vas a hallar las coordenadas de un vector respecto de una base que no es ortogonal. | + | |descripcion=En esta escena podrás ver como es el producto escalar de vectores ortogonales. |
| + | |enlace=[https://ggbm.at/Pw67JAKs Producto escalar de vectores ortogonales] | ||
| + | }} | ||
| + | |||
| + | ===Módulo de un vector en una base ortonormal=== | ||
| + | {{Teorema||titulo=Proposición (9)|enunciado= | ||
| + | El módulo de un vector {{sube|porcentaje=+10%|contenido=<math>\vec{v}(v_1,v_2)</math>}}, respecto de una base otonormal, es | ||
| + | |||
| {{p}} | {{p}} | ||
| - | |actividad= | + | <center><math>|\vec{v}|=\sqrt{v_1^2+v_2^2}</math></center> |
| - | <center><iframe> | + | |demo=Si {{sube|porcentaje=+10%|contenido=<math>\vec{v}=(v_1,v_2)</math>}} respecto de una base otonormal, entonces, por la proposición (7): |
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_2.html | + | |
| - | width=450 | + | |
| - | height=410 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | Halla las coordenadas del vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{u},\overrightarrow{v})</math>}}: | + | <center><math>\vec{v} \cdot \vec{v}=v_1 \, v_1 + v_2 \, v_2=v_1^2+v_2^2</math></center> |
| - | #Hay que formar un paralelogramo con las prolongaciones de los vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} (Variando '''a''' y '''b'''), de tal forma que {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} sea una diagonal del mismo. Por tanto esta vez, te conviene prolongar {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} en el sentido opuesto y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} en su mismo sentido. | + | Por otro lado sabemos, por la cuarta propiedad de (3), que: |
| - | #A continuación tienes que trazar paralelas a {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} desde el extremo de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}}, '''A''', para completar el paralelogramo. | + | |
| - | #Escribe en tu cuaderno {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} como combinación lineal de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}. | + | |
| - | #Escribe las coordenadas de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{u},\overrightarrow{v})</math>}}. | + | |
| + | <center><math>\vec{v} \cdot \vec{v}=|\vec{v}|^2</math></center> | ||
| + | |||
| + | Igualando ambos resultados tenemos lo que buscamos. | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Dado el vector {{sube|porcentaje=+10%|contenido=<math>\vec{u}(2,-1)</math>}}, respecto de una base otonormal, vamos a calcular {{sube|porcentaje=+10%|contenido=<math>|\vec{u}|</math>}}: | ||
| + | |||
| + | :<math>|\vec{u}|=\sqrt{2^2+(-1)^2}=\sqrt{5}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Módulo de un vector|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=6'16" | ||
| + | |sinopsis=Módulo de un vector. | ||
| + | |url1=https://youtu.be/e0t3cQujJC4?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| }} | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Tutorial 2a | ||
| + | |duracion=6´18" | ||
| + | |url1=https://www.youtube.com/watch?v=OQ0mmEVw4hI&index=8&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A | ||
| + | |sinopsis= | ||
| + | *Módulo de un vector. | ||
| + | *Ejemplos. | ||
| {{p}} | {{p}} | ||
| - | ==Operaciones con coordenadas== | + | Nota: En la segunda parte del video se trata el caso de vectores tridimensionales. |
| - | {{Caja_Amarilla|texto= | + | |
| - | Sean {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}=(x_1,y_1)</math>}} y {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{v}=(x_2,y_2)</math>}} dos vectores del plano: | + | |
| - | *'''Suma de vectores:''' {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}+\overrightarrow{v}=(x_1+x_2,y_1+y_2)</math>}} | + | |
| - | *'''Producto por un número k:''' {{sube|porcentaje=+25%|contenido=<math>k \overrightarrow{u}=(k \, x_1,k \, y_1)</math>}} | + | |
| - | *'''Combinación lineal:''' {{sube|porcentaje=+25%|contenido=<math>a \overrightarrow{u}+b \overrightarrow{v}=(a \, x_1+ b \, x_2, a \, y_1+b \, y_2)</math>}} | + | |
| }} | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Tutorial 2b | ||
| + | |duracion=9´45" | ||
| + | |url1=https://www.youtube.com/watch?v=cfe-IS-gNoU&index=10&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A | ||
| + | |sinopsis= | ||
| + | *Vector unitario. | ||
| + | *Ejemplos de como calcularlos. | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Operaciones con coordenadas''|cuerpo= | + | Nota: En la segunda parte del video se trata el caso de vectores tridimensionales. |
| - | {{ai_cuerpo | + | }} |
| - | |enunciado='''Actividad 1:''' Coordenadas de la suma de dos vectores. | + | {{Video_enlace_fonemato |
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=14´13" | ||
| + | |url1=https://www.youtube.com/watch?v=_5Q6MkBK9xg&list=PL811F7AF8E8EC9655&index=11 | ||
| + | |sinopsis= | ||
| + | *Módulo de un vector. | ||
| + | *Ejemplos. | ||
| + | *Vectores unitarios. | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Tutorial 4 (Normalización de vectores) | ||
| + | |duracion=12´53" | ||
| + | |url1=https://youtu.be/9xSoSG-VT24?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Vectores unitarios. Normalización de vectores. Ejemplos. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=6´25" | ||
| + | |url1=https://www.youtube.com/watch?v=Rmx9LqcFLO8&index=16&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A | ||
| + | |sinopsis=Dados los vectores <math>\vec{u}=(5,-12)</math> y <math>\vec{v}=(-3,-6)</math>, calcula: | ||
| + | :a)<math>|\vec{u}|</math> | ||
| + | :b)<math>|\vec{v}|</math> | ||
| + | :c)<math>|\vec{u}-\vec{v}|</math> | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=4´02" | ||
| + | |url1=https://www.youtube.com/watch?v=ULSVQ7AIaJc&index=22&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A | ||
| + | |sinopsis=Encontrar un vector unitario en la dirección del vector <math>3\vec{i}+7\vec{j}</math>. | ||
| {{p}} | {{p}} | ||
| - | |actividad= | + | Nota: <math>B=\{\vec{i},\vec{j}\}</math> es la base canónica de los vectores del plano. |
| - | Comprueba en la siguiente escena como se obtienen las coordenadas de la suma de dos vectores respecto de la base ortonormal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | + | }} |
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=5'11" | ||
| + | |sinopsis=Calcula el perímetro de un triángulo conocidas las coordenadas de sus vértices. | ||
| + | |url1=https://youtu.be/YHX62KCS1SQ?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'11" | ||
| + | |sinopsis=Cálculo del módulo y de la dirección de vectores del plano. | ||
| + | |url1=https://youtu.be/dxtlmyPXvvo?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Vectores unitarios | ||
| + | |descripcion=Ejercicios de autoevaluación sobre vectores unitarios. | ||
| + | |url1=http://www.vitutor.com/geo/vec/b_1_e_2.html | ||
| + | }} | ||
| + | {{wolfram desplegable|titulo=Módulo de un vector|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Módulo de un vector'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado=Halla el módulo del vector <math>\vec{u} =(3,5)</math>. | ||
| - | <center><math>\overrightarrow{u}=(-2,3) \, \quad \overrightarrow{v}=(5,2) \quad \rightarrow \quad \overrightarrow{u}+\overrightarrow{v}=(-2+5,3+2)=(3,5)</math></center> | + | |sol= |
| + | Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: | ||
| - | <center><iframe> | + | {{consulta|texto=lenght vector (3,5)}} |
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_3.html | + | |
| - | width=450 | + | |
| - | height=410 | + | {{widget generico}} |
| - | name=myframe | + | }} |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | }} |
| - | '''Ejercicio:''' | ||
| - | Cambia el valor de los controles o mueve con el ratón los extremos de {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} para comprobar la suma para las siguientes coordenadas: {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=(-4,0)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(4,3)</math>}} | ||
| }} | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' Coordenadas de la combinación lineal de dos vectores. | ||
| {{p}} | {{p}} | ||
| - | |actividad= | ||
| - | Comprueba en la siguiente escena como se obtienen las coordenadas de la combinación lineal de dos vectores, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=(-2,2)</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=(-3,1)</math>}},respecto de la base ortonormal {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | ||
| - | <center><math>1.5 \overrightarrow{u}+2 \overrightarrow{v}=1.5 \, (-2,2)+ 2 \, (-3,-1)=(-3,3)+(-6,2)=(-9,1)</math></center> | + | ===Ángulo de dos vectores en una base ortonormal=== |
| + | {{Teorema||titulo=Proposición (9)|enunciado= | ||
| + | Dados dos vectores, {{sube|porcentaje=+10%|contenido=<math>\vec{u}(u_1,u_2)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}(v_1,v_2)</math>}}, respecto de una base otonormal, se cumple que | ||
| + | {{p}} | ||
| + | <center><math>cos \, (\widehat{\vec{u}, \, \vec{v}})=\cfrac{u_1 \, v_1 + u_2 \, v_2}{\sqrt{u_1^2+u_2^2} \, \sqrt{v_1^2+v_2^2}}</math></center> | ||
| - | Este resultado lo puedes ver en la escena, si haces '''a=1.5''' y '''b=2''' | + | |demo=Si {{sube|porcentaje=+10%|contenido=<math>\vec{u}=(u_1,u_2)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}=(v_1,v_2)</math>}}, respecto de una base otonormal, entonces: |
| - | <center><iframe> | + | <center><math>\vec{u} \cdot \vec{v}=u_1 \, v_1 + u_2 \, v_2 \qquad |\vec{u}|=\sqrt{u_1^2+u_2^2} \qquad |\vec{v}|=\sqrt{v_1^2+v_2^2}</math></center> |
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_4.html | + | |
| - | width=450 | + | |
| - | height=410 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores5_4.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | '''Ejercicio:''' | + | Por otro lado: |
| - | Calcula en tu cuaderno las coordenadas, respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, de los vectores: | + | <center><math>\vec{u} \cdot \vec{v}=|\vec{u}| \, |\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}}) \quad \rightarrow \quad cos \, (\widehat{\vec{u}, \, \vec{v}})=\cfrac{\vec{u} \cdot \vec{v}}{|\vec{u}| \, |\vec{v}|}</math></center> |
| - | '''a)''' {{sube|porcentaje=+30%|contenido=<math>-\overrightarrow{u}-\overrightarrow{v}</math>}} | + | Sustituyendo en esta última expresión las anteriores, tenemos lo que buscamos. |
| - | '''b)''' {{sube|porcentaje=+30%|contenido=<math>2 \overrightarrow{u}-1.5 \overrightarrow{v}</math>}} | + | |
| }} | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Dados los vectores {{sube|porcentaje=+10%|contenido=<math>\vec{u}(2,-1)</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{v}(3,2)</math>}}, respecto de una base otonormal, vamos a calcular el ángulo que forman: | ||
| + | |||
| + | :<math>cos \, (\widehat{\vec{u}, \, \vec{v}})=\cfrac{\vec{u} \cdot \vec{v}}{|\vec{u}| \, |\vec{v}|}=\cfrac{4}{\sqrt{5} \, \sqrt{13}}=0.4961 \quad \rightarrow \quad \widehat{\vec{u}, \, \vec{v}}=60^\circ 15' 20''</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Ángulo de dos vectores en una base ortonormal|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=9´31" | ||
| + | |url1=https://youtu.be/FyJLPLM7YeE?list=PLwCiNw1sXMSAMNnvvsBGpp778cpwcoDuV | ||
| + | |sinopsis=Producto escalar y ángulo entre dos vectores. Ejemplos. | ||
| + | }} | ||
| + | {{Video_enlace_pablo | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=10´00" | ||
| + | |url1=https://youtu.be/HDmcAi5MJPM?list=PLDofgcGDlFDP3PLa5X06SC7w-njU6albc | ||
| + | |sinopsis=Ángulo entre dos vectores del plano. Perpendicularidad. Ejemplos. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=5´35" | ||
| + | |url1=https://www.youtube.com/watch?v=jBoNqb6auhQ&index=48&list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9A | ||
| + | |sinopsis=Halla el ángulo que forman los vectores <math>\vec{A}=(4,3)</math> y <math>\vec{B}=(5,-2)</math> | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=9´05" | ||
| + | |url1=https://www.youtube.com/watch?v=Y53RziXh2UM&list=PL811F7AF8E8EC9655&index=26 | ||
| + | |sinopsis=3 ejercicios sobre ángulo entre dos vectores. | ||
| + | }} | ||
| + | }} | ||
| + | {{wolfram desplegable|titulo=Ángulo entre vectores|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Ángulo entre vectores'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado=Halla el ángulo que forman los vectores <math>\vec{u} =(3,5)</math> y <math>\vec{v} =(2,1)</math>. | ||
| + | |||
| + | |sol= | ||
| + | Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: | ||
| + | |||
| + | {{consulta|texto=angle between vectors (3,5), (2,1)}} | ||
| + | |||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Producto escalar con bases ortonormales'' | ||
| + | |cuerpo= | ||
| + | (Pág. 178) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 6 | ||
| + | |||
| + | }} | ||
| + | |||
| + | ==Producto escalar de vectores (enfoque alternativo)== | ||
| + | En estos videotutoriales se va partir de la proposición (7) como definición de producto escalar y se va a deducir como resultado la definición de la que hemos partido al comienzo de este capítulo. | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Producto escalar de vectores (enfoque alternativo)|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Producto escalar de vectores | ||
| + | |duracion=8´12" | ||
| + | |url1=https://www.youtube.com/watch?v=rU_J2qPNioA&list=PL811F7AF8E8EC9655&index=20 | ||
| + | |sinopsis= | ||
| + | *El "producto escalar" de los vectores <math>\vec{u} = (u_1;u_2)</math> y <math>\vec{v} = (v_1;v_2)</math> es el número real <math>u_1 \cdot v_1 + u_2 \cdot v_2</math>. Se denota <math>\vec{u} \cdot \vec{v}</math>. | ||
| + | *Dos vectores se dicen "ortogonales" si su producto escalar es 0. | ||
| + | *Dos vectores se dicen "ortonormales" si son ortogonales y tienen módulo 1. | ||
| + | *Al final del vídeo está la letanía que debes recitar a modo de mantra cuando aterrices en la Universidad. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=4 ejercicios | ||
| + | |duracion=6´07" | ||
| + | |url1=https://www.youtube.com/watch?v=-mTMQKWPyK0&list=PL811F7AF8E8EC9655&index=21 | ||
| + | |sinopsis=En este video jugamos con la suma de vectores y con el producto escalar de vectores. | ||
| + | }} | ||
| + | |||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Propiedades del producto escalar | ||
| + | |duracion=5'56" | ||
| + | |url1=https://www.youtube.com/watch?v=xomwigWaaPI&list=PL811F7AF8E8EC9655&index=23 | ||
| + | |sinopsis=VEl producto escalar goza de las propiedades conmutativa, asociativa mixta y distributiva respecto de la suma. El producto escalar de un vector por sí mismo es el cuadrado del módulo del vector. | ||
| + | No es admisible que las propiedades del producto escalar de vectores te dejen con el culo al aire. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=6 ejercicios | ||
| + | |duracion=10´31" | ||
| + | |url1=https://www.youtube.com/watch?v=y_8K1e3hTQA&list=PL811F7AF8E8EC9655&index=24 | ||
| + | |sinopsis=6 ejercicios sobre las propiedades del producto escalar. | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Angulo entre dos vectores | ||
| + | |duracion=9´28" | ||
| + | |url1=https://www.youtube.com/watch?v=9gzLIBQQKY0&list=PL811F7AF8E8EC9655&index=25 | ||
| + | |sinopsis=El coseno del ángulo que forman dos vectores es el cociente entre el producto escalar de los vectores y el producto de los módulos de los vectores. | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | ==Producto escalar en el espacio tridimensional (Ampliación)== | ||
| + | {{p}} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Producto escalar de dos vectores en el espacio | ||
| + | |duracion=19´58" | ||
| + | |url1=https://youtu.be/Vkj9w304n5o | ||
| + | |sinopsis=En el siguiente vídeo condensamos todo lo que hemos visto a lo largo de esta página sobre el producto escalar de vectores, pero trabajando con vectores tridimensionales. No obstante, lo que se explican son conceptos generales aplicables a vectores del plano. | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Act. Interactivas | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Producto escalar de vectores
Se llama producto escalar de dos vectores 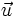 y
y 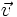 , al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
, al número real que se obtiene multiplicando los módulos de ambos vectores por el coseno del ángulo que forman:
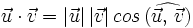
Como dos vectores forman dos ángulos entre sí, tomaremos el menor de ellos. De todas formas, para el cálculo del producto escalar da igual que tomemos uno u otro, ya que ambos ángulos son opuestos y, por tanto, tienen el mismo coseno.
Vídeo que condensa los resultados más importantes que se van a desarrollar a lo largo de esta página sobre el producto escalar de dos vectores en el plano.
Propiedades del producto escalar
Propiedad fundamental del producto escalar
Propiedades (1)
- Si
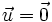 ó
ó 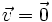 entonces
entonces 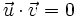 .
.
-
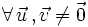 se cumple que
se cumple que 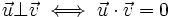
- La primera propiedad es inmediata.
- Para la segunda propiedad, si ambos vectores no son nulos, entonces, el producto escalar es cero si y solo si el coseno del ángulo que forman es cero, y esto ocurre si sólo si el ángulo es de 90º ó -90º.
- Dos vectores son perpendiculares si y sólo si su producto escalar es cero
- Ejemplos.
Nota: A lo largo del video también se ven ejemplos con vectores tridimensionales.
Signo del producto escalar
Propiedades (2)
El signo del producto escalar queda determinado por el ángulo que forman los vectores:
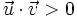 si
si 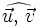 es agudo.
es agudo.
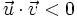 si
si 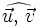 es obtuso.
es obtuso.
Esta propiedad es inmediata, ya que el coseno de un ángulo es positivo, si éste es agudo, y negativo, si es obtuso.
En esta escena podrás ver como se calcula el producto escalar de vectores y cómo es su signo.
Propiedades del producto escalar
Propiedades (3)
- Conmutativa:
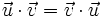
- Asociativa mixta:

- Distributiva:
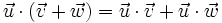
- Propiedad conmutativa:
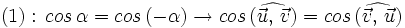
- Propiedad asociativa:
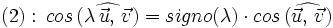 , ya que el ángulo es igual si
, ya que el ángulo es igual si 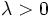 y suplementario si
y suplementario si 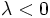 .
.
- (Recuerda que ángulos suplementarios tienen cosenos opuestos).
- Así tenemos una de las igualdades:
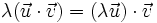 . La otra igualdad se obtendría de forma similar.
. La otra igualdad se obtendría de forma similar.
- Propiedad distributiva:
- Obteniendo la igualdad buscada.
- La última propiedad es fácil:
Proyección de vectores y producto escalar
Llamaremos proyección del vector 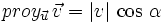 siendo Observa que la proyección es un número positivo o negativo según lo sea Gráficamente es como la sombra (ver segmento rojo en figura adjunta) que proyecta Aquí la proyección se define como un escalar (la medida del segmento rojo de la figura de la derecha). Otras veces, la proyección se define como el vector que determina la sombra tomando como origen, el origen común de los dos vectores, y como extremo, el de la intersección con la línea discontinua perpendicular al vector 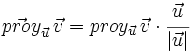 |
Proposición (4)
El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él.
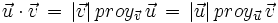
En consecuencia:
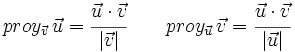
Si observamos el dibujo de la derecha, tenemos que
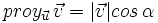
Entonces
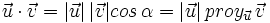
De la misma manera se obtiene la otra relación:
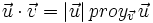
Proyección de vectores y producto escalar. Ejemplos.
Sean 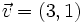 y
y 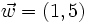 . Halla el vector proyección
. Halla el vector proyección 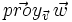 y su módulo, es decir,
y su módulo, es decir, 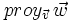 .
.
Corolario (5): Proyecciones coincidentes Si las proyecciones sobre 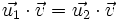 Demostración:  En esta escena podrás ver como se representa y calcula la proyección de un vector sobre otro. |
Ejercicios propuestos
|
Ejercicios propuestos: Producto escalar |
El producto escalar con bases ortonormales
Expresión analítica del producto escalar en bases ortonormales
Proposición (6)
Sea 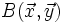 una base ortonormal, entonces
una base ortonormal, entonces
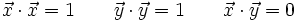
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
Proposición (7)
Si las coordenadas de los vectores 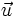 y
y 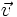 , respecto de una base otonormal
, respecto de una base otonormal 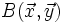 son
son 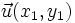 y
y 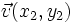 , entonces:
, entonces:
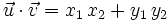
En efecto, al ser los vectores de la base unitarios y perpendiculares, tenemos:
- Base canónica.
- Cálculo del producto escalar de vectores del plano en la base canónica.
- Cálculo del producto escalar de vectores del plano.
- Ejemplos.
Nota: A lo largo del video también se trata el caso de vectores tridimensionales.
En esta escena podrás ver como se representa el producto escalar de dos vectores.
Vector ortogonal a otro
Proposición (8)
Los vectores de coordenadas 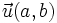 y
y 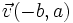 , respecto de una base ortonormal, son ortogonales.
, respecto de una base ortonormal, son ortogonales.
Por la propiedad fundamental, sabemos que:
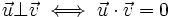
Por otro lado, como las base es ortonormal, la expresión analítica del producto escalar es

Halla 3 vectores ortogonales a (2,3).
Solución: Por la proposición anterior: (-3,2).
Cualquier múltiplo de (-3,2) también será ortogonal: (3,-2) y (-6,4)
Ejemplo:
Calcula el valor de 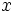 para que el vector
para que el vector 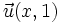 sea ortogonal a
sea ortogonal a 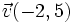 , respecto de una base ortonormal.
, respecto de una base ortonormal.
Al venir dadas las coordenadas respecto de una base ortonormal, para que los vectores dados sean ortogonales, su producto escalar debe ser cero:
Producto escalar de vectores ortogonales. Obtención de un vector ortogonal a uno dado. Ejemplos.
En esta escena podrás ver como es el producto escalar de vectores ortogonales.
Módulo de un vector en una base ortonormal
Proposición (9)
El módulo de un vector 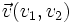 , respecto de una base otonormal, es
, respecto de una base otonormal, es
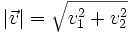
Si 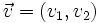 respecto de una base otonormal, entonces, por la proposición (7):
respecto de una base otonormal, entonces, por la proposición (7):
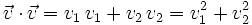
Por otro lado sabemos, por la cuarta propiedad de (3), que:
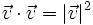
Módulo de un vector.
- Módulo de un vector.
- Ejemplos.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
- Vector unitario.
- Ejemplos de como calcularlos.
Nota: En la segunda parte del video se trata el caso de vectores tridimensionales.
- Módulo de un vector.
- Ejemplos.
- Vectores unitarios.
Vectores unitarios. Normalización de vectores. Ejemplos.
Dados los vectores 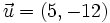 y
y 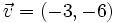 , calcula:
, calcula:
- a)
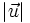
- b)
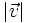
- c)
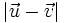
Encontrar un vector unitario en la dirección del vector 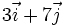 .
.
Nota: 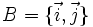 es la base canónica de los vectores del plano.
es la base canónica de los vectores del plano.
Calcula el perímetro de un triángulo conocidas las coordenadas de sus vértices.
Cálculo del módulo y de la dirección de vectores del plano.
Ejercicios de autoevaluación sobre vectores unitarios.
Ángulo de dos vectores en una base ortonormal
Proposición (9)
Dados dos vectores, 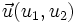 y
y 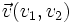 , respecto de una base otonormal, se cumple que
, respecto de una base otonormal, se cumple que
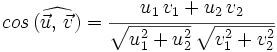
Si 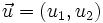 y
y 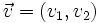 , respecto de una base otonormal, entonces:
, respecto de una base otonormal, entonces:
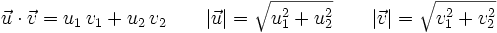
Por otro lado:
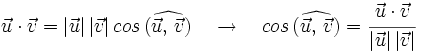
Dados los vectores 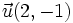 y
y 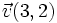 , respecto de una base otonormal, vamos a calcular el ángulo que forman:
, respecto de una base otonormal, vamos a calcular el ángulo que forman:
Producto escalar y ángulo entre dos vectores. Ejemplos.
Ángulo entre dos vectores del plano. Perpendicularidad. Ejemplos.
Halla el ángulo que forman los vectores 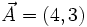 y
y 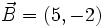
3 ejercicios sobre ángulo entre dos vectores.
Ejercicios propuestos
|
Ejercicios propuestos: Producto escalar con bases ortonormales |
Producto escalar de vectores (enfoque alternativo)
En estos videotutoriales se va partir de la proposición (7) como definición de producto escalar y se va a deducir como resultado la definición de la que hemos partido al comienzo de este capítulo.
- El "producto escalar" de los vectores
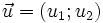 y
y 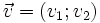 es el número real
es el número real 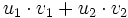 . Se denota
. Se denota 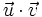 .
.
- Dos vectores se dicen "ortogonales" si su producto escalar es 0.
- Dos vectores se dicen "ortonormales" si son ortogonales y tienen módulo 1.
- Al final del vídeo está la letanía que debes recitar a modo de mantra cuando aterrices en la Universidad.
En este video jugamos con la suma de vectores y con el producto escalar de vectores.
VEl producto escalar goza de las propiedades conmutativa, asociativa mixta y distributiva respecto de la suma. El producto escalar de un vector por sí mismo es el cuadrado del módulo del vector. No es admisible que las propiedades del producto escalar de vectores te dejen con el culo al aire.
6 ejercicios sobre las propiedades del producto escalar.
El coseno del ángulo que forman dos vectores es el cociente entre el producto escalar de los vectores y el producto de los módulos de los vectores.
Producto escalar en el espacio tridimensional (Ampliación)
En el siguiente vídeo condensamos todo lo que hemos visto a lo largo de esta página sobre el producto escalar de vectores, pero trabajando con vectores tridimensionales. No obstante, lo que se explican son conceptos generales aplicables a vectores del plano.
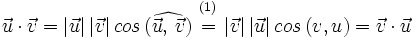
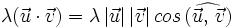
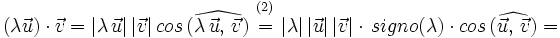
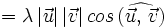

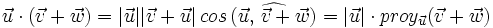
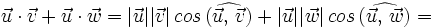
![=|\vec{u}|[|\vec{v}| \, cos \, (\widehat{\vec{u}, \, \vec{v}})+|\vec{w}| \, cos \, (\widehat{\vec{u}, \, \vec{w}})]=](/wikipedia/images/math/f/3/b/f3b89089f996e680f6647e40232d1b7a.png)
![=|\vec{u}| \cdot [proy_\vec{u} \vec{v}+proy_\vec{u} \vec{w}]=|\vec{u}| \cdot [proy_\vec{u} (\vec{v}+ \vec{w})]](/wikipedia/images/math/a/4/6/a466b34f8c309d0f85cdbd073cd479e5.png)
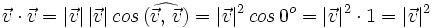
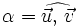
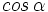 .
.
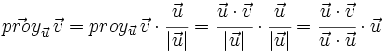
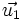
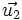
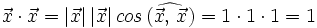
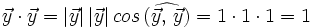
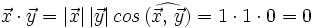
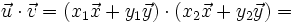
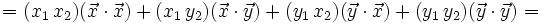
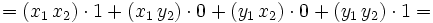
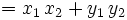
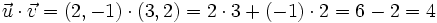
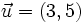 y
y 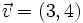 . Halla el producto escalar
. Halla el producto escalar  para que los vectores
para que los vectores 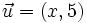 y
y 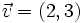 sean ortogonales.
sean ortogonales.
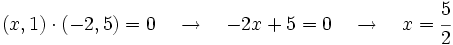
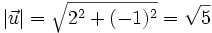
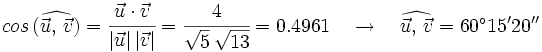
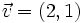 .
.
