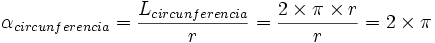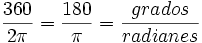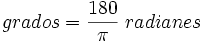Ángulos. Medidas (PACS)
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Trigonometría (ppt) | WIRIS Calculadora |
Tabla de contenidos |
Ángulo
Se denomina ángulo, en el plano, a la porción de éste comprendida entre dos semirrectas que tienen un origen común denominado vértice. Coloquialmente, ángulo es la figura formada por dos rayos con origen común. Así, un ángulo determina una superficie abierta (subconjunto abierto de puntos del plano), al estar definido por dos semirrectas, denominándose medida del ángulo a la amplitud de estas semirrectas.
Las unidades de medida de ángulos
Las unidades utilizadas para la medida de los ángulos del plano son:
- Radián (usado oficialmente en el sistema internacional de unidades)
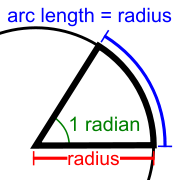
El radián se define como el ángulo que limita un arco de circunferencia cuya longitud es igual al radio de la circunferencia. Una definición más general, indica que el ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco formado sobre el radio, es decir, θ = s /r, donde θ es el ángulo, s es la longitud del arco y r es el radio. Por tanto, el ángulo, α, completo en radianes de una circunferencia de radio, r, es:
Su símbolo es rad.
- Grado sexagesimal
El grado sexagesimal, como unidad del sistema de medida de ángulos sexagesimal, esta definido partiendo de que un ángulo recto tiene 90° (90 grados sexagesimales), y sus divisores el minuto sexagesimal, y el segundo sexagesimal, están definidos del siguiente modo:
- 1 ángulo recto = 90° (grados sexagesimales).
- 1 grado sexagesimal = 60′ (minutos sexagesimales).
- 1 minuto sexagesimal = 60″ (segundos sexagesimales).
Notación decimal
Una cantidad en grados se puede expresar en forma decimal, separando la parte entera de la decimal con la coma decimal, en la forma normal de expresar cantidades decimales, por ejemplo.
- 23,2345°
- 12,32°
- -50,265°
- 123,696°
Notación sexagesimal
Podemos expresar una cantidad en grados minutos y segundos, las partes de grado inferiores al segundo se expresan como parte decimal de segundo, ejemplo:
- 12°34′34″
- 13°3′23,8″
- 124°45′34,70″
- -2°34′10″
Teniendo cuidado como norma de notación, no dejar espacio entre las cifras, es decir:
escribir 12°34′34,2″ y no 12° 34′ 34″
Relación ente radianes y grados sexagesimales
Se parte de la base de que una circunferencia completa tiene 2π radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
luego tenemos que:
La tabla muestra la conversión de los ángulos más comunes.
| Grados | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
Clasificación de ángulos planos
Ángulo agudo
Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de 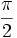 rad (mayor de 0º y menor de 90º).
rad (mayor de 0º y menor de 90º).
Al punto de inicio o de encuentro, se le llama vértice.
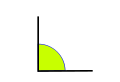
Ángulo recto
- Un ángulo recto es de amplitud igual a
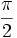 rad (equivalente a 90º).
rad (equivalente a 90º).
- Un ángulo recto es de amplitud igual a
- Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
- Los dos lados de un ángulo recto son perpendiculares entre sí.
Ángulo obtuso
Un ángulo obtuso es aquel cuya amplitud es mayor a 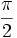 rad y menor a
rad y menor a 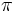 rad (mayor a 90º y menor a 180º).
rad (mayor a 90º y menor a 180º).
Ángulo llano o extendido
El ángulo llano tiene una amplitud de 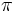 rad (equivalente a 180º).
rad (equivalente a 180º).
Ángulo cóncavo o reflejo
El ángulo cóncavo, externo o reflejo, es el que mide más de 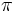 rad y menos de
rad y menos de 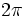 rad (esto es, más de 180º y menos de 360°)
rad (esto es, más de 180º y menos de 360°)
Ángulo completo o perigonal
Un ángulo completo o perigonal, tiene una amplitud de 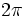 rad (equivalente a 360º)
rad (equivalente a 360º)