Ángulos en los polígonos (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ángulos interiores y exteriores
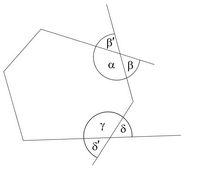
En el dibujo de la derecha, el ángulo |
Polígonos cóncavos y convexos
- Un polígono es convexo si todos sus ángulos interiores miden menos de 180º.
- Un polígono es cóncavo si alguno de sus ángulos interiores mide más de 180º.
Ángulos en un triángulo
Propiedad
Los tres ángulos interiores de un triángulo suman 180º.
Demostración de que la suma de los ángulos de un triángulo es un ángulo llano (180º).
En esta escena podrás ver como se obtiene la suma de los ángulos triángulo.
Ejemplos que ilustran la propiedad de que la suma de los ángulos internos de un triángulo es 180º.
Los ángulos de un triángulo miden 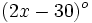 ,
, 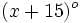 y
y 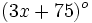 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un cuadrilátero
Propiedad
Los cuatro ángulos interiores de un cuadrilátero suman 360º.
En la siguiente escena de Geogebra.
En esta escena podrás ver como se calcula la suma de los ángulos interiores de un cuadrilátero.
Halla el ángulo que falta en los siguientes cuadriláteros.
Halla los ángulos que faltan en los siguientes cuadriláteros.
Halla el ángulo que falta en el siguiente cuadrilátero.
Los ángulos de un cuadrilátero miden 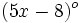 ,
, 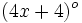 ,
, 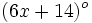 y
y 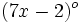 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un polígono de n lados
Propiedades
- La suma de los ángulos interiores de un polígono de
 lados es igual a
lados es igual a 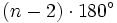 .
.
- Si el polígono de
 lados es regular:
lados es regular:
- Cada ángulo interior mide
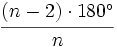 .
.
- Cada ángulo exterior mide
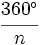 .
.
- Cada ángulo interior mide
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
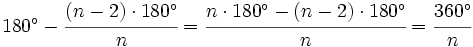
- Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular.
Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Suma de los ángulos interiores de un polígono.
- Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de su suma.
Ángulos interiores de un cuadrado y de un hexágono regular.
¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulo exterior de un polígono regular
Actividades
Ejercicios de autoevaluación sobre los ángulos en los polígonos.
Ejercicios de autoevaluación sobre los ángulos en los polígonos.
 es interno y los ángulos
es interno y los ángulos 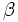 y
y 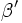 son sus correspondientes ángulos externos.
son sus correspondientes ángulos externos.