Diofanto

De Wikipedia

Portada de la obra de Diofanto, Arithmetica

Diofanto de Alejandría (c. 200 - c. 284) fue un antiguo matemático griego, considerado el padre del álgebra.

Vida

Nacido en Alejandría, nada se conoce con seguridad sobre su vida salvo la edad a la que falleció, gracias a este epitafio redactado en forma de problema y conservado en la antología griega:

"Transeúnte, esta es la tumba de Diofanto: es él quien con esta sorprendente distribución te dice el número de años que vivió. Su niñez ocupó la sexta parte de su vida; después, durante la doceava parte su mejilla se cubrió con el primer bozo. Pasó aún una séptima parte de su vida antes de tomar esposa y, cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole, durante cuatro años. De todo esto se deduce su edad."

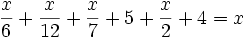
donde es la edad que vivió Diofanto

Según esto, Diofanto falleció a la edad de 84 años. Se ignora, sin embargo en qué siglo vivió. Si es el mismo astrónomo Diofanto que comentó Hipatia (fallecida en 415), habría fallecido antes del siglo V, pero si se trata de personas distintas cabe pensar que vivía a finales de dicho siglo, ya que ni Proclo ni Pappus le citan, lo que resulta difícil de entender tratándose de un matemático que pasa por ser el inventor del álgebra. En opinión de Albufaraga, Diofanto vivía en los tiempos del emperador Juliano, hacia el año 365, fecha que aceptan los historiadores.

Obra

Aritmetica, su gran obra

El matemático alejandrino debe su renombre a su obra Aritmetica. Este libro, que constaba de trece libros de los que sólo se han hallado seis. Los libros que faltan parece que se perdieron tempranamente ya que no hay razones para suponer que los traductores y comentaristas árabes dispusieran de otros manuscritos además de los que aún se conservan.

Fue traducido al latín por Bombelli en 1570, pero la traducción no se publicó. Sin embargo, Bombelli prestado muchos de los problemas de su propio libro de álgebra. La primera traducción publicada fue la de Guilielmus Xylander en 1575 a partir de unos manuscritos de la universidad de Wittenberg, añadiendo el editor un manuscrito sobre números poligonales, fragmento de otro tratado del mismo autor. La traducción latina de Arithmetica más conocida es la que hizo Bachet en 1621, que se convirtió en la primera edición latina ampliamente disponible. Pierre de Fermat poseía una copia, la estudió e hizo anotaciones en sus márgenes. Una edición reimpresa con posterioridad en 1670 por el hijo de Fermat, incluía los comentarios que el célebre matemático francés había realizado en los márgenes de su ejemplar de la edición de Bachet. En una de dichas anotaciones se exponía, sin demostración, el último teorema de Fermat. En el precioso ejemplar de la edición de Bachet que Fermat poseía, él dijo "haber encontrado una gran luz".

En esta obra realiza sus estudios de ecuaciones con variables que toman valores racionales, las ecuaciones diofánticas, aunque no es una obra de carácter teórico sino una colección de problemas. En el uso moderno, las ecuaciones diofánticas son ecuaciones algebraicas con coeficientes enteros, para lo cual se buscan soluciones enteras. El estudio de las ecuaciones diofánticas y de las aproximaciones diofánticas siguen siendo aspectos importantes de la investigación matemática.

Diofanto fue el primer matemático griego que reconoció a las fracciones como números.

Notación matemática

Importante fue también su contribución en el campo de la notación. Si bien los símbolos empleados por Diofanto no son como los concebimos actualmente, introdujo importantes novedades como el empleo de un símbolo único para la variable desconocida (στ) y para la sustracción, aunque conservó las abreviaturas para las potencias de la incógnita (δς para el cuadrado, δδς para el duplo del cuadrado, χς para el cubo, δχς para la quinta potencia, etc.).

Análisis diofántico

Actualmente, el análisis diofántico es el área de estudio donde se buscan soluciones enteras para las ecuaciones, y las ecuaciones diofánticas son aquellas ecuaciones polinómicas con coeficientes enteros de las que sólo se buscan soluciones enteras. Por lo general, es bastante difícil decir si una determinada ecuación diofántica tiene solución. La mayoría de los problemas en Aritmetica llevaban a ecuaciones cuadráticas. Diofanto consideró 3 tipos diferentes de ecuaciones de segundo grado:

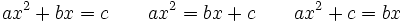
La razón por la cual él consideró tres casos, mientras que hoy sólo tenemos uno, es que él no tenía ninguna noción de cero y que evitaba los coeficientes negativos, considerando que los números a, b, c eran positivos en cada uno de los tres casos anteriores. Diofanto siempre se quedaba satisfecho con una solución racional y no requería un número entero como solución, aceptando las fracciones como soluciones a sus problemas. Diofanto considera las soluciones negativas y las raíces cuadradas irracionales como "inútiles", "sin sentido" e incluso "absurdas". Para dar un ejemplo concreto, que él llama a la ecuación 4 = 4x + 20 "absurda" porque conduciría a un valor negativo de x. El sólo buscaba una solución en las ecuaciones de segundo gardo. No hay evidencia que sugiera que Diofanto alguna vez se diera cuenta de que podía haber dos soluciones en una ecuación cuadrática. También consideró ecuaciones cuadráticas simultaneas.

Otras obras

Diofanto escribió varias obras además de Aritmetica, pero muy pocas han sobrevivido.

• Los Porismas

Diofanto se refiere a un trabajo que consiste en una colección de lemas llamados Los Porismas (o Porismata), pero este libro se perdió por completo. Algunos estudiosos piensan que Los Porismas pueden haber sido realmente una sección de Aritmetica que se perdió.

Aunque Los Porismas se perdieron, conocemos tres de sus lemas porque Diofanto se refiere a ellos en Aritmetica. Uo de los lemas dice que la diferencia de los cubos de dos números racionales es igual a la suma de los cubos de otros dos números racionales, es decir:

"Dados y , , 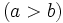existen y 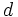, todos positivos y racionales, tales que: "

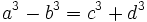• Números poligonales y elementos geométricos

Se sabe que Diofanto también escribió sobre números poligonales, tema de gran interés para Pitágoras y los pitagóricos.

• Preliminares a los Elementos Geométricos

Un libro llamado Preliminares a los Elementos Geométricos ha sido atribuido tradicionalmente a Herón de Alejandría. Recientemente, estudios de Wilbur Knorr, sugieren que el autor real es Diofanto.