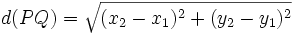Distancia entre dos Puntos (4ºESO-B)
De Wikipedia
Distancia entre dos puntos
Conocidas las coordenadas de dos puntos del plano, el teorema de Pitágoras nos permite calcular la distancia entre ambos:
Proposición
La distancia entre dos puntos 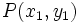 y
y 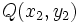 es igual a:
es igual a:
|
|
Demostración:
Ver el siguiente videotutorial.- Módulo de un vector = distancia entre dos puntos. Demostración de la fórmula.
- Ejemplos y ejercicios.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
- Fórmula de la distancia euclidea entre dos puntos del plano. Ejemplos.
- Otra distancia: la "distancia de Manhattan".
Cálculo de distancias:
Halla la distancia entre los puntos A(7,3) y B(3,-1).
Halla la distancia entre los puntos A(3,1/2) y B(4/3,-1).
Halla la distancia entre los puntos A(3/2,-1/6) y B(-1/2,1/3).
Halla la distancia entre los puntos 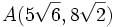 y
y 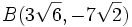 .
.
Halla la distancia entre los puntos 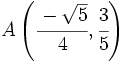 y
y 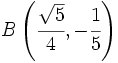 .
.
Halla la coordenada que falta:
Halla el valor de "x" para que la distancia entre los puntos A(x,-1) y B(9,4) sea 13.
Halla el valor de "y" para que la distancia entre los puntos P(7,1) y Q(3,y) sea 5.
Halla el punto Q el eje Y que equidista de A(4,2) y B(5,5).
Halla el punto P el eje X que equidista de A(5,1) y B(0,6).
Halla el punto P que equidista de A(7,-3), B(8,-2) y C(0,-2).
La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P.
Sean los puntos M(5,2) y N(1,k). Determina "k" en cada uno de los siguientes casos:
a) d(M,N)=4; b) d(M,N)=6; c) d(M,N)=1
Polígonos:
Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1).
Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1).
Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón.
Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón.
Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos 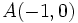 ,
, 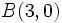 y
y 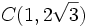 forman un triángulo equilátero.
forman un triángulo equilátero.
Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles.
Analizar si el triángulo A(7,3), B(1,-4) y C(3,5) es equilátero.
Puntos colineales:
Determina si los puntos A(-3,1), B(0,2) y C(6,4) son colineales, usando distancias.
Determina si los puntos A(321), B(0,0) y C(9,6) son colineales, usando distancias.
Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias.
Otros:
Determina los puntos del plano cuya distancia al punto M(3,-5) sea 2.
En esta escena podrás ver como se calcula la distancia entre dos puntos del plano.