Distribuciones bidimensionales. Nubes de puntos. Correlación (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Distribuciones bidimensionales
Una distribución bidimensional o de dos variables es aquella en la que para cada elemento de la población o muestra se consideran dos caracteres cuantitativos distintos, 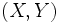 . Así, a cada individuo le corresponden los valores de dos variables que representamos mediante el par ordenado
. Así, a cada individuo le corresponden los valores de dos variables que representamos mediante el par ordenado 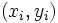 , siendo
, siendo 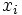 el valor del primer carácter e
el valor del primer carácter e 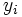 el del segundo.
el del segundo.
Ejemplos: Distribuciones bidimensionales
- Notas obtenidas en las asignaturas de Matemáticas y Física por los alumnos de una clase.
- Estatura y peso de los alumnos del instituto.
Nube de puntos
Si representamos cada par 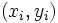 de valores de una distribución bidimensional como un punto del plano, obtendremos lo que se llama una nube de puntos o diagrama de dispersión. A partir de ella podemos observar como se relacionan las dos variables de forma intuitiva.
de valores de una distribución bidimensional como un punto del plano, obtendremos lo que se llama una nube de puntos o diagrama de dispersión. A partir de ella podemos observar como se relacionan las dos variables de forma intuitiva.
Nota: Si algún par de puntos se repite, el punto correspondiente de la nube se representará con mayor grosor, proporcional al número de repeticiones.
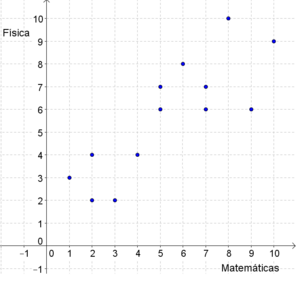
En el anterior ejemplo sobre las notas de Matemáticas y Física, teníamos la siguiente tabla de observaciones:
| Matemáticas (X) | 3 | 2 | 5 | 1 | 7 | 6 | 2 | 4 | 8 | 9 | 5 | 10 | 7 |
| Física (Y) | 2 | 2 | 6 | 3 | 6 | 8 | 4 | 4 | 10 | 6 | 7 | 9 | 7 |
Su correspondiente nube de puntos será:
Diagrama de dispersión o nube de puntos. Ejemplos de distintos tipos de nubes.
Correlación
A partir de la nube de puntos podemos observar como se relacionan las dos variables. Si al aumentar o disminuir una de ellas, aumenta o disminuye la otra de forma sistemática, diremos que existe correlación entre las dos variables.
La correlación puede ser:
- Fuerte: Si hay mayor alineamiento de los puntos de la nube.
- Débil: Si el alineamiento es menor, hay mas "dispersión" de los puntos.
La correlación (fuerte o débil), además puede ser:
- Positiva: Si al aumentar X aumenta Y
- Negativa: Si al aumentar X, disminuye Y
La correlación más o menos fuerte viene, por tanto, determinada por lo apretados que estén los puntos de la nube en torno a una recta que llamaremos recta de regresión. El signo de la pendiente de esta recta determina si la correlación es positiva (pendiente positiva) o negativa (pendiente negativa).
En el anterior ejemplo, las notas de Matemáticas y Física mantienen una correlación positiva ya que al aumentar las de Matemáticas, aumentan las de Física. Además es una correlación relativamente fuerte dado el alineamiento de los puntos.
Entre dos variables estadísticas unidimensionales puede existir una relación funcional, una relación estadística o ninguna relación. Además, de existir una relación estadística, esta puede ser fuerte o débil.
|
Actividad: Nube de puntos y recta de regresión de distribuciones bidimensionales
(X,Y)=(Matemáticas,Física)={(3,2),(2,2),(5,6),(1,3),(7,6),(6,8),(2,4),(4,4),(8,10),(9,6),(5,7),(10,9),(7,7)}
(X,Y)=(Distancia, Hoyos)={(1,10),(2,10),(4,8),(6,7),(8,6),(10,3),(12,4),(15,3),(18,1),(20,0)}
Solución: Para averiguar las solución debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
WolframAlpha utilizará el método de mínimos cuadrados para hallar la recta de regresión. Este método lo estudiaremos más adelante. |
|
Actividad Interactiva: Nube de puntos y recta de regresión de distribuciones bidimensionales La siguiente escena muestra una nube de puntos y una tabla con las notas obtenidas por 12 alumnos en las asignaturas de Lengua Española (X) y Literatura (Y). Mueve los puntos de la nube y observa como afecta a la correlación. También puedes ver la recta de regresión marcando la casilla correspondiente. Puedes añadir o quitar puntos de la tabla y adapatar la escena para otras variables bidimensionales que quieras. Puedes cambiar los valores de las notas para adaptarlo al ejemplo de las notas de Matemáticas y Física o al ejemplo del jugador de golf que vimos anteriormente. |