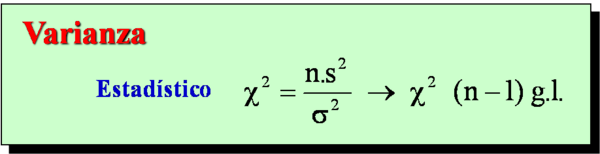Estadísticos
De Wikipedia
| Ir a | Para repasar | Para ampliar | Enlaces externos |
| Indice Casio | {{{ampliar}}} | WIRIS Calculadora Descartes |
Tabla de contenidos |
Introducción
La estadística nos proporciona herramientas que formalizan y uniforman los procedimientos para sacar conclusiones siempre que las muestras seleccionadas sean representativas de la población que han sido extraídas. Esta representatividad permite extender los valores que describen a las muestras (estadísticos), tales como la media, la desviación típica, un coeficiente de correlación, a la población correspondiente, es decir, la media o la desviación típica (estadísticos) pueden tomarse como estimadores de los parámetros μ y σ, valores que caracterizan a la población.
Los estadísticos, valores obtenidos en la muestra, son, pues, estimadores de los parámetros correspondientes (valores de la población)
Características de los estimadores
Conviene que los estadísticos, en su función de estimadores de los correspondientes parámetros, reúnan determinados requisitos. Fundamentalmente son:
- a)CARENCIA DE SESGO.
Un estimador (estadístico) carece de sesgo si el promedio (media) de todos los valores posibles de todas las muestras posibles de tamaño n de una población es igual al parámetro, es decir, si la media de la distribución muestral del estadístico considerado es igual al valor del parámetro. Así, la media es un estimador insesgado de μ porque se puede demostrar que la media aritmética de una distribución muestral coincide con el valor del parámetro, algo que no puede decirse, por ejemplo, o de la varianza o de la mediana de una población no distribuida normalmente.
- b) CONSISTENCIA.
Un estimador es consistente en la medida en que, al aumentar el tamaño de la muestra, (n) su valor se acerca cada vez más al parámetro correspondiente o lo que es lo mismo, si a medida que aumenta el tamaño de la muestra, las estimaciones que ésta proporciona son cada vez más próximas al valor del parámetro.
Algunos estimadores sesgados son consistentes, acercándose cada vez más sus valores a los de sus respectivos parámetros a medida que el tamaño de la muestra (n) aumenta, tal es el caso de s o s2 que son estimadores sesgados pero consistentes de la desviación típica (σ) o de la varianza (σ2) de la población.
- c) EFICIENCIA
La 3ª propiedad de los estimadores es su eficiencia, que se refiere a la precisión que alcanzan los estadísticos en la estimación de los parámetros, es decir, un estimador será tanto más eficiente cuanto menos varíe de muestra a muestra de una misma población. Como la variabilidad de una distribución muestral viene dada por su error típico, un buen estimador será aquel que menor error típico alcanza. Así, entre la media y la mediana, la primera es claramente más eficiente. La varianza de la distribución muestral de la mediana es mayor que la de la media, lo que significa que la mediana fluctúa más que la media en muestras sucesivas de la misma población.
En general, para escoger un óptimo estimador de un parámetro, deben combinarse los criterios de no tendenciosidad (carencia de sesgo) y de eficiencia. Ante dos estimadores insesgados del mismo parámetro, se preferirá aquel que tenga mayor eficiencia, es decir, que tenga el mínimo error en términos de varianza.
- • Estimadores insesgados: Media, Mediana, Moda, la desviación típica cuando n es tiende a infinito, la cuasivarianza muestral
- • Estimadores sesgados: la varianza muestral.
- • Estimadores consistentes: Proporciones, la media, la varianza y desviación típìca.
- • Estimadores insesgados y no eficientes: Mediana muestral (estimador insesgado de μ]

|
Actividad 1 |
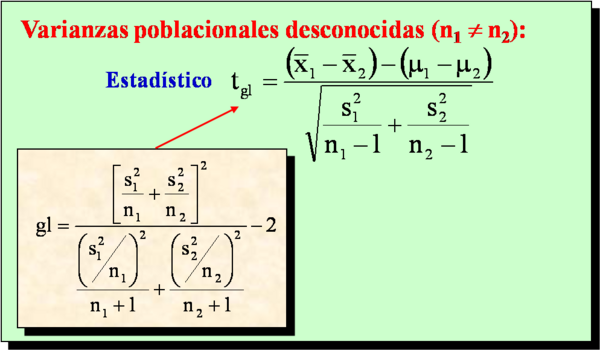
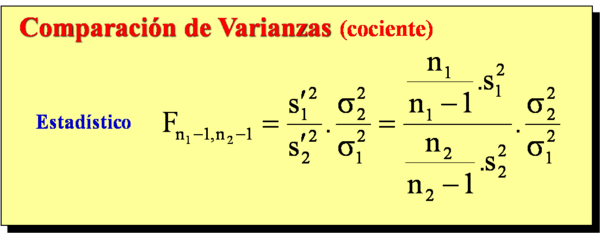
Ejemplos de estadísticos