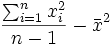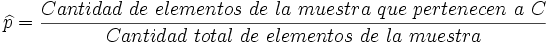Estimación puntual
De Wikipedia
| Ir a | Para repasar | Para ampliar | Enlaces externos |
| Indice Casio | WIRIS Calculadora Descartes |
Tabla de contenidos |
Introducción
Puede decirse que la Estadística es la ciencia que se preocupa de la recogida de datos, su organización y análisis, así como de las predicciones que, a partir de estos datos, pueden hacerse. Los aspectos anteriores hacen que pueda hablarse de dos tipos de Estadística: Descriptiva e Inferencial.
La Estadísitica Descriptiva se ocupa de tomar los datos de un conjunto dado, organizarlos en tablas o representaciones gráficas y del cálculo de unos números que nos informen de manera global del conjunto estudiado.
La Estadística Inferencial estudia cómo sacar conclusiones generales para toda la población a partir del estudio de una muestra.
Existen dos formas de hacer Inferencia Estadística:
- La estimación de parámetros.
- Las pruebas de hipótesis.
En la Inferencia Estadística hay varios métodos, pero en cualquier caso es necesario utilizar una muestra que represente a la población, esto se consigue con las Técnicas de muestreo.
A partir de una muestra nos proponemos dos objetivos:
- Obtener valores aproximados de parámetros poblacionales: Estimación puntual.
- La estimación por intervalos de confianza tiene por objeto proporcionar, a partir de la información recogida en la muestra, un intervalo que contenga con alto nivel de confianza (probabilidad), al parámetro objeto de nuestro interés. A partir de dicho intervalo obtendremos una medida del error máximo cometido al aproximar puntualmente el parámetro.
Estimación puntual
Esencialmente son tres los parámetros de interés:
- En el caso de que investiguemos una variable cuantitativa:
- a) Para la media de la población μ tomaremos como aproximación la media de la muestra.
|
|
- b) Para la varianza de la población σ2 tomaremos la cuasivarianza de la muestra.
|
|
- Si el estudio se centra en el estudio de un carácter cualitativo el parámetro de interés será la proporción de elementos de la población que pertenecen a cierta categoría C que lo aproximaremos con la correspondiente proporción en la muestra.
|
|
|
Actividades Interactivas:Estimación puntual Actividad 1.Se sabe que la longitud en centímetros de una determinada especie de coleópteros sigue una distribución normal. Capturados varios ejemplares de dicha especie, sus longitudes fueron: 6 ejemplares de 1.85 m; 6 ejemplares de 2.71 m; 5 ejemplares de 2.91 m; 8 ejemplares de 2.7 m; 9 ejemplares de 2.64 m; 5 ejemplares de 3.25 m; Vamos a aproximar la media y la varianza de la población. Introduce los datos en la escena y se calcularán ambas aproximaciones. Pasa los datos obtenidos a tu cuaderno de trabajo. Observar que el valor de la media es la suma de todos los datos dividido entre el tamaño de la muestra. Y que el valor de la cuasivarianza es la suma de todos los datos al cuadrado dividido entre el tamaño de la muestra menos la media al cuadrado.Actividad: Actividad 2. En una región se seleccionó aleatoriamente una muestra de 120 personas. A todas ellas se les preguntó si fumaban o no. 36 contestaron que no. A partir de dicha información, vamos a estimar el porcentaje de fumadores en dicha región. Introduce los datos en la escena siguiente y se obtendrá la aproximación. Observa que basta dividir el número de fumadores entre el total de la muestra. Pasa los datos obtenidos a tu cuaderno de trabajo.Actividad: |
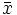 =
= 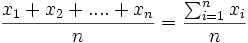
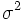 =
=