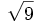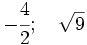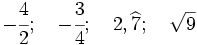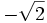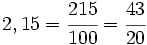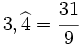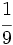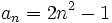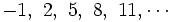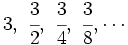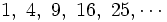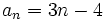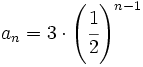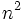Examen: Los números y sus utilidades I y II; Progresiones (Ene 08)
De Wikipedia
|
Examen: Los números y sus utilidades I y II; Progresiones (Ene 08) Ejercicio 1: (1,5 ptos) 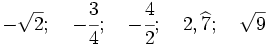 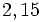 y y 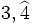 Solución: a)
b) Ejercicio 2: (1,5 ptos) 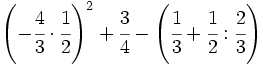
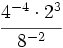 Solución: a)  Ejercicio 3: (1,5 ptos) Solución: a) 288 €, 403,2 € y 316,8 € Ejercicio 4: (2 ptos) a) En unos zapatos de 65 € nos aplican un descuento del 15%. Calcula el precio que pagamos por los zapatos. b) Se han pagado 1202 € por un ordenador. Si el IVA aplicado ha sido del 16%, ¿cuál era el precio inicial del ordenador?Solución: a) 55,25 € b)1036,21 € Ejercicio 5: (2 ptos) a) Escribe los cinco primeros términos de la sucesión b) Calcula el término general de las sucesiones:
Solución: a) 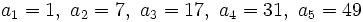
b)
Ejercicio 6: (1,5 ptos) a) ¿Cuántos ejercicios realizó cada uno de los primeros cinco días? b)¿Cuántos ejercicios le tocará hacer al cabo de 100 días? c) ¿Cuántos ejercicios hará en total esos 100 días?Solución: a) 1, 3, 5, 7, 9 ejercicios b) 199 ejercicios c) 10000 ejercicios |