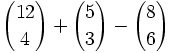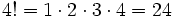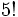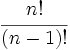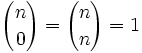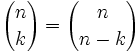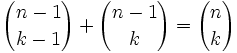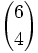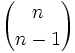Factoriales y números combinatorios (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 43)
Factoriales
Sea 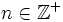 , se define el factorial de
, se define el factorial de  como
como
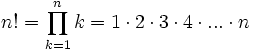
y se define, por convenio:
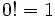 .
.La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en combinatoria y análisis matemático. De manera fundamental el factorial de n representa el número de formas distintas de ordenar n objetos distintos (permutaciones). Este hecho ya era conocido en el siglo XII por los hindúes.
La notación matemática actual, 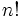 , fue usada por primera vez en 1808 por Christian Kramp (1760–1826), un matemático francés que trabajó, en especial, sobre los factoriales durante toda su vida.
, fue usada por primera vez en 1808 por Christian Kramp (1760–1826), un matemático francés que trabajó, en especial, sobre los factoriales durante toda su vida.
El factorial de un número. Ejemplos. Obtención del factorial de un número con la calculadora.
Calcula 10!
Calcula 8!
Calcula 5!
Factorial de un número. Ejemplos.
a) Halla "x": 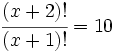
b) Halla "a": 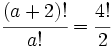
a) Calcula 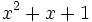 sabiendo que
sabiendo que 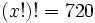
b) Simplifica: 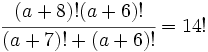
a) Halla "a": 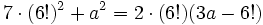
b) Halla "x": 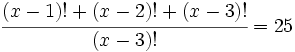
(Pág. 43)
Números combinatorios
Coeficiente binomial
Sean 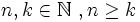 . Se llama coeficiente binomial, y lo representaremos por
. Se llama coeficiente binomial, y lo representaremos por 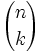 , al número de subconjuntos de
, al número de subconjuntos de  elementos escogidos de un conjunto con
elementos escogidos de un conjunto con  elementos. Se lee "n sobre k".
elementos. Se lee "n sobre k".
También se suele decir que es el "número de combinaciones de  elementos tomados de
elementos tomados de  en
en  " y, por tanto, que se le conozca también como "número combinatorio".
" y, por tanto, que se le conozca también como "número combinatorio".
Proposición
El coeficiente binomial viene dado por la fórmula:
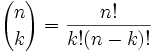
Demostración:
Si se tiene un conjunto con n elementos, de los cuales se van a escoger k de ellos, la selección (ordenada) puede hacerse de
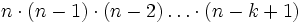
formas, ya que en el primer paso se tienen n opciones, en el segundo se tienen n-1, en el tercero n-2, y así sucesivamente, terminando en el paso k que tendrá n-k+1 opciones.
Ahora, para eliminar los conjuntos repetidos, hay que dividir el producto anterior entre el número de selecciones "equivalentes" (conjuntos con los mismos elementos en distinto orden). Pero si se tiene k objetos, hay k! formas de permutarlos, es decir, k! formas de listarlos en distinto orden.
Concluimos que el número de subconjuntos con k elementos, escogidos de un conjunto con n elementos es
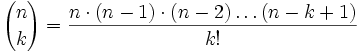
Multiplicando el numerador y el denominador por 
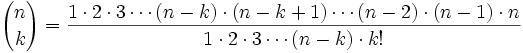
o lo que es lo mismo, expresado con factoriales:
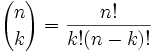
Propiedades de los números combinatorios
Propiedades
Demostración:
- En un conjunto con n elementos se puede extraer sólo un conjunto con 1 elemento (sólo el
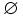 ) y solo un conjunto con n elementos (el propio conjunto de partida).
) y solo un conjunto con n elementos (el propio conjunto de partida).
- En un conjunto con n elementos, cada subconjunto con k elementos tiene un complementario con n-k elementos.
- Esta demostración podéis verla en el siguiente vídeo:
Demostración de las propiedades de los números combinatorios.
Los 8 últimos minutos de este tutorial tratan sobre números combinatorios.
Ejemplos de cálculo de números combinatorios. Obtención con la calculadora.
Ejemplos de cálculo de números combinatorios.
Calcula: 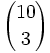
Calcula: 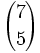
Calcula: 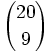
Comprueba que: 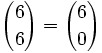
Comprueba que: 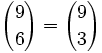
Comprueba que: 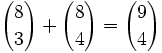
Calcula: