Funciones: Crecimiento, Máximos y Mínimos (4ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
(Pág. 89)
Tabla de contenidos |
Crecimiento y variación de una función
- Una función es creciente en un intervalo I cuando al aumentar la variable independiente
 en ese intervalo, aumenta la variable dependiente
en ese intervalo, aumenta la variable dependiente  .
.
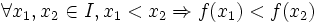
- Una función es decreciente en un intervalo cuando al aumentar la variable independiente
 en ese intervalo, disminuye la variable dependiente
en ese intervalo, disminuye la variable dependiente  .
.
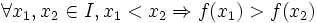
- Una función es constante en un intervalo cuando al aumentar la variable independiente
 en ese intervalo, la variable dependiente
en ese intervalo, la variable dependiente  no varía, siempre toma un mismo valor
no varía, siempre toma un mismo valor  .
.
Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
Conceptos de función creciente, decreciente y constante.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Actividades con las que aprenderás a determinar los intervalos de crecimiento y decrecimiento de una función.
En esta escena podrás ver cuando una función es creciente, decreciente o constante.
Determina los intervalos de crecimiento y decrecimiento de una función.
Se llama variación de una función  en un intervalo
en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) , a lo que varía la variable dependiente de un extremo a otro del intervalo:
, a lo que varía la variable dependiente de un extremo a otro del intervalo:
![\Delta f_{[a,b]}=f(b)-f(a)\;](/wikipedia/images/math/f/1/e/f1ebdfa1d125fb540c0cf9d9b00d9152.png)
Extremos relativos de una función
- Una función
 tiene un máximo relativo en un punto
tiene un máximo relativo en un punto 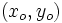 cuando
cuando 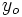 es mayor que los valores que toma la variable
es mayor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
- Una función
 tiene un mínimo relativo en un punto
tiene un mínimo relativo en un punto 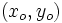 cuando
cuando 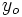 es menor que los valores que toma la variable
es menor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
Tutorial en el que se explica el estudio de máximos y mínimos (relativos y absolutos) de una función dada su gráfica.
Tutorial en el que se explica el estudio de máximos y mínimos (relativos y absolutos) de una función dada su gráfica.
Conceptos de máximo y mínimo relativos.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Actividades con las que aprenderás a determinar los máximos y mínimos de una función dada gráficamente.
En esta escena podrás ver cuando una función alcanza un máximo o un mínimo.
Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. Averigua sus máximos y mínimos relativos.
Construye una gráfica que cumpla ciertas condiciones sobre los puntos por los que pasa. Se exigira, por ejemplo, que tenga máximos o mínimos en ciertos puntos, que tenga ciertos puntos de corte con los ejes, etc.
Unos alumnos de E.S.O. disponen de una cuerda de 80 metros de longitud con la que quieren construir rectángulos en el patio de su centro.
- Haz una tabla de valores donde se relacione la base de los rectángulos y su área.
- Representa gráficamente la función.
- Halla una expresión que te permita calcular el área de cualquiera de esos rectángulos, conocida su base.
- ¿Cuál es el dominio de esta función?
- ¿Para qué valor del lado se consigue un rectángulo de área máxima? ¿Qué tiene de peculiar ese valor?
Máximos y mínimos relativos o locales.
Máximos y mínimos absolutos.
|
Actividad: Extremos relativos Nota para los cursos de secundaria: Algunas de las siguientes actividades son sólo ilustrativas ya que su resolución manual requiere conocimientos de 1º de bachillerato.
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Actividades y videotutoriales
Interpreta la gráfica dada.
Interpreta la gráfica dada.
Problemas verbales de interpretación de gráficas.
|
Ejercicios resueltos: Crecimiento. Máximos y mínimos |
Ejercicios propuestos
|
Ejercicios propuestos: Crecimiento, Máximos y Mínimos |
Tasa de variación media
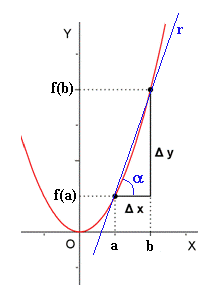
Para medir el crecimiento medio de una función en un intervalo [a,b], se utiliza la tasa de variación media (T.V.M.) o tasa de cambio, que se define como el cociente de la variación de y entre la variación de x:
Si hacemos
Proposición La T.V.M. de una función en un intervalo |
- Definición de tasa de variación media de una función.
- Ejemplo a partir de la gráfica de la función.
- Ejemplo a partir de la expresión analítica de la función.
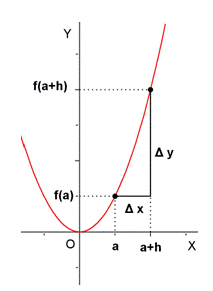
- Definición de tasa de variación media o tasa de cambio de una función f en el intervalo [a,a+h].
- Interpretación geométrica.
- Ejemplos
Algunos ejemplos que relacionan el concepto de tasa de variación media con el de velocidad media.
Tasa de variación media de una recta
Tasa de variación media de una parábola. Interpretación con un ejemplo de la vida cotidiana.
Calcula la T.V.M. de f(x) = x2 + 2; en [1,4].
Calcula la T.V.M. de:
- a) d(t) = 3t + 1; en [0,1] y [1,2].
- b) d(t) = t2 + 1; en [0,3] y [2,3].
A partir de la gráfica, determina el intervalo en el cual la T.V.M. de la función es -4.
A partir de la tabla, determina la T.V.M. de la función en el intervalo [-5, -2].
Dada la función 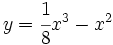 , ¿sobre cuál de los siguientes intervalos tiene T.V.M. igual a 1/2: [-2, 2], [0, 4], [-3, 2], [-4, 1] ?
, ¿sobre cuál de los siguientes intervalos tiene T.V.M. igual a 1/2: [-2, 2], [0, 4], [-3, 2], [-4, 1] ?
Cálcula la T.V.M. de 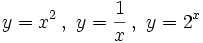 en el intervalo [x, x+h].
en el intervalo [x, x+h].
Problema sobre el cálculo de la tasa de variación media a partir de una tabla.
Problema sobre el cálculo de la tasa de variación media a partir de una gráfica.
Problema sobre el cálculo de la tasa de variación media.
Tasa de variación media.
En esta escena podrás calcular la T.V.M. de la función que tú quieras.
Tasa de variación media.
Problemas verbales sobre la tasa de variación media.
Ejercicios propuestos
|
Ejercicios propuestos: Tasa de variación media |
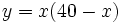
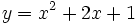
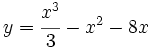 .
.
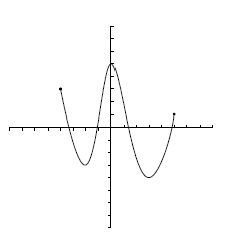
![[-2, 0] \cup [3, 5]\;\!](/wikipedia/images/math/0/1/2/012762c2d4663dd7895b4f06b3648f3b.png)
![[-4, -2] \cup [0, 3]\;\!](/wikipedia/images/math/9/8/5/98539f209bd8b0dbd0bc02fec7106551.png)
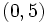
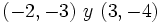
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(b)-f(a)}{b-a}](/wikipedia/images/math/8/9/c/89c85ce438b13f83f07e3480026d5be8.png)
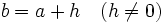 , la expresión anterior queda como sigue:
, la expresión anterior queda como sigue:
![T.V.M._f \,[a,a+h]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(a+h)-f(a)}{h}](/wikipedia/images/math/c/8/1/c81e647a1a3e3e683857d6714eed390f.png)
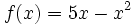 , su T.V.M. en el intervalo [1,2] es:
, su T.V.M. en el intervalo [1,2] es:
![T.V.M._f \,[1,2]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(2)-f(1)}{2-1}=\cfrac{6-4}{1}=2](/wikipedia/images/math/1/4/1/141dc581dee9a22c26e10a24407de907.png)
 y
y  .
.
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=tg\, \alpha=m](/wikipedia/images/math/6/b/7/6b761a6a89fc5990f82ffd9ae6ec3b0e.png)
 es la pendiente de la recta r.
es la pendiente de la recta r.