Funciones Logarítmicas (4ºESO Académicas)
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
[editar]
Funciones logarítmicas
Sea 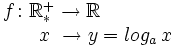
|
[editar]
Propiedades de la función logarítmica
Propiedades de la función logarítmica Las funciones exponenciales de base
|
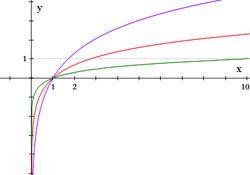
Representación de la familia de funciones logarítmicas.
Representación conjunta de las funciones logarítmica y exponencial.
[editar]
Utilidad de la función logarítmica
[editar]
Ejercicios propuestos
|
Ejercicios propuestos: Funciones logarítmicas |
 . Se define la función logarítmica de base
. Se define la función logarítmica de base  como:
como:
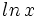 .
.
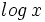 (sin especificar la base).
(sin especificar la base).
 .
.
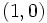 y
y 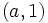 .
.
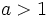 son crecientes.
son crecientes.
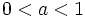 son decrecientes.
son decrecientes.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
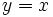 .
.