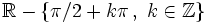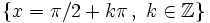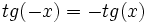Funciones trigonométricas. El radián (4ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
El radián
Equivalencia entre radianes y grados sexagesimales
Equivalencia entre radianes y grados sexagesimales
|
|
En consecuencia:

Como la longitud de una circunferencia de radio
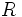 es
es 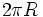 , tenemos que una circunferencia contiene
, tenemos que una circunferencia contiene 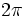 veces a la radio. Por tanto, 360º equivalen a
veces a la radio. Por tanto, 360º equivalen a 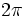 rad y , dividiendo por 2, 180º equivalen a
rad y , dividiendo por 2, 180º equivalen a 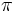 rad.
rad.Utilizando la equivalencia anterior, y mediante una regla de tres, podemos obtener las siguientes equivalencias:
| Grados | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
Equivalencia entre grados sexagesimales y radianes.
El sistema radial o circular. Equivalencias con el sistema sexagesimal.
Ejemplos:
- Expresa el ángulo 32,56º (32 grados y 56 centésimas de grado) en grados, minutos y segundos.
- Expresa el ángulo 46º15'36" en grados sexagesimales.
- Expresa el ángulo 2,6 rad. en grados, minutos y segundos.
- Expresa en radianes el ángulo 72º.
Introducción a los radianes.
Conversión entre radianes y grados. Ejemplos.
Conversión entre radianes y grados. Ejemplos.
Convertir grados sexagesimales a radianes:
Expresa 200º en radianes.
Expresa 135º en radianes.
Expresa 45.32º en radianes.
Expresa 16.142º en radianes.
Expresa 132º 42' 37" en radianes.
Expresa 12º 45" en radianes.
Expresa 750º en radianes.
Expresa 150º y -45º en radianes.
Convertir radianes a grados sexagesimales:
Expresa 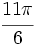 radianes en grados.
radianes en grados.
Expresa 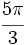 radianes en grados.
radianes en grados.
Expresa 8 radianes en grados.
Expresa 0.5 radianes en grados.
Expresa 5.214 radianes en grados.
Expresa 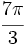 radianes en grados.
radianes en grados.
Expresa 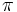 radianes y
radianes y 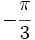 radianes en grados.
radianes en grados.
Otros ejercicios:
Indica en que cuadrante está cada uno de los siguientes ángulos: 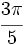 radianes,
radianes, 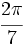 radianes y 3 radianes.
radianes y 3 radianes.
Conversión ente grados a radianes.
Ejercicios de autoevaluación sobre equivalencia entre radianes y grados sexagesimales.
Ejercicios de autoevaluación sobre equivalencia entre radianes y grados sexagesimales.
Ejercicios propuestos
|
Ejercicios propuestos: El radián |
Funciones trigonométricas
Vamos a estudiar las funciones que se obtienen a partir de las razones trigonométricas de un ángulo x al hacer variar éste. Dicho ángulo se suele expresar en radianes.
En esta escena podrás ver como se representan las funciones trigonométricas.
Estudio gráfico de las funciones seno y coseno.
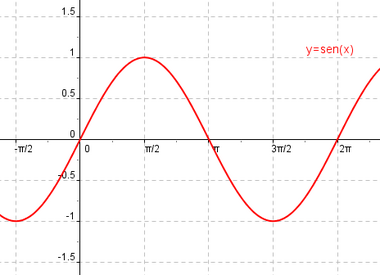
Función seno
Se define la función seno como 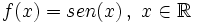 |
Definición, representación y análisis de la función seno.
Definición, representación y análisis de la función seno. Ejercicios.
Dominio, rango y representación de la función seno.
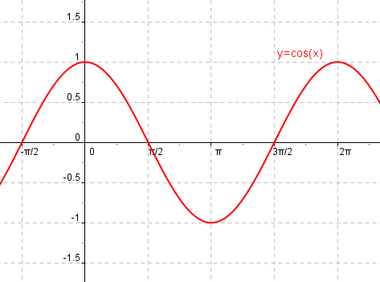
Función coseno
Se define la función coseno como 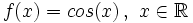 |
Definición, representación y análisis de la función coseno.
Definición, representación y análisis de la función coseno. Ejercicios.
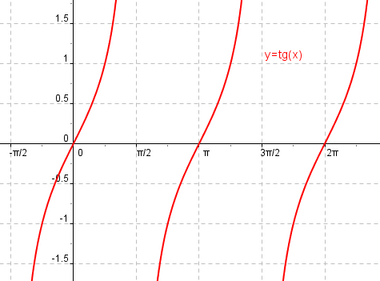
Función tangente
Se define la función coseno como 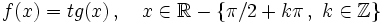 Propiedades de la función tangente
|
Definición, representación y análisis de la función tangente. Ejercicios.
Representación de la función tangente
Ejercicios propuestos
|
Ejercicios propuestos: Funciones trigonométricas. El radián |
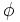 mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
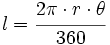
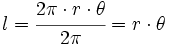
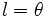
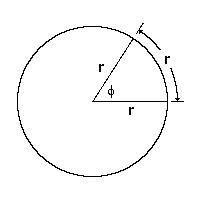
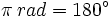

![[-1, 1]\,](/wikipedia/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png)
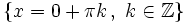
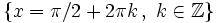

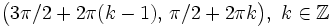 .
.
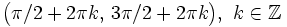 .
.
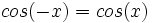
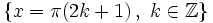
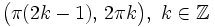 .
.
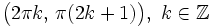 .
.