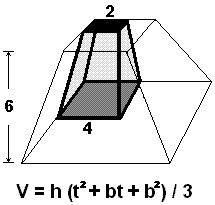Las matemáticas en Mesopotamia y antiguo Egipto (c. 1800-500 a.C.)

De Wikipedia

Mesopotamia

Las matemáticas babilónicas se refieren a la de los pueblos de Mesopotamia (Irak moderno) desde los días de los primeros sumerios hasta el comienzo del período helenístico. El nombre de matemáticas babilónicas es debido al papel central de Babilonia como un lugar de estudio, que dejó de existir durante el período helenístico. Desde este punto, la matemática babilónica se fusionó con las matemáticas griegas y egipcias para dar lugar a las matemáticas helenísticas. Más tarde, bajo el imperio árabe, Irak (Mesopotamia), especialmente Bagdad, una vez más se convirtió en un importante centro de estudio de la matemática islámica.

Tabla de arcilla mesopotámica, fechada en el año 492 a.C.

En contraste con la escasez de fuentes egipcias en matemáticas, el conocimiento de las matemáticas babilonicas se deriva de más de 400 tablillas de arcilla descubiertas desde 1850. Escritas en escritura cuneiforme, las tablillas se inscribieron mientras la arcilla estaba húmeda, y posteriormente horneadas en un horno o por el calor del sol.

La primera prueba escrita de matemáticas se remonta a los antiguos sumerios, que crearon la primera civilización de Mesopotamia. Estos desarrollaron un complejo sistema de medida desde el 3000 a.C. Desde alrededor de 2500 a.C. en adelante, los sumerios escribieron tablas de multiplicar en tablillas de arcilla y realizaron ejercicios geométricos y problemas de divisiones. Los primeros rastros de los números de Babilonia también se remontan a este período.

La mayoría de las tablillas de arcilla recuperadas datan de 1800 a 1600 a.C., y abarcan temas que incluyen fracciones, álgebra, ecuaciones cuadráticas, cúbicas y el cálculo de ternas pitagóricas. La tablilla mesopotámica Plimpton 322, que data de 1900 a.C., registra un número de ternas pitagóricas, y aunque esto no sea una formulación abstracta del teorema de Pitágoras, se adelantó milenios a éste. Las tablillas también contienen tablas de multiplicar, tablas trigonométricas y métodos para resolver ecuaciones lineales y cuadráticas. La tablilla babilónica YBC 7289 da una aproximación de $\sqrt{2}$ con una precisión de cinco decimales.

Las matemáticas babilónicas fueron escritas utilizando un sistema de unumeración sexagesimal (base 60). De esto se deriva el uso actual de los 60 segundos en un minuto, 60 minutos en una hora, y 360 (60 x 6) grados en un círculo. Los avances babilónicos en matemáticas se vieron facilitados por el hecho de que el 60 tiene muchos divisores. Además, a diferencia de los egipcios, griegos y romanos, los babilonios tenían un verdadero sistema posicional, donde los dígitos escritos en la columna de la izquierda representa los valores más grandes, como en el sistema decimal. Ellos carecían, sin embargo, un equivalente del punto decimal, por lo que el valor posicional de un símbolo, a menudo, tenía que ser deducido por el contexto.

[editar]

Egipto

Volumen del tronco de pirámide

Las matemáticas egipcias se refieren a aquellas escritas en el idioma egipcio. A partir del período helenístico, el griego sustituyó al egipcio como lengua escrita de los estudiosos de Egipto, y desde este punto las matemáticas egipcias se fusionaron con las griegas y las babilonicas para dar lugar a las matemáticas helenísticas. El estudio matemático en Egipto más tarde continuó bajo el imperio árabe como parte de las matemáticas islámicas, cuando el árabe se convirtió en la lengua escrita de los estudiosos de Egipto.

El papiro de Moscú es el texto matemático más antiguo descubierto hasta ahora. Es un papiro del Imperio Medio egipcio, de la dinastía XII, que data de c. 2000-1800 a.C. Con cinco metros de longitud y tan sólo ocho centímetros de anchura consta de 25 problemas matemáticos, aunque algunos se encuentran demasiado dañados para poder ser interpretados. El papiro fue escrito en escritura hierática por un escriba egipcio desconocido, que no era tan meticuloso como Ahmes, el escriba del papiro Rhind. Se desconoce el objetivo con el que fue escrito. Al igual que muchos antiguos textos matemáticos, se compone de lo que hoy se denomina "problemas de palabra" o "problemas historia", destinados, al parecer, al entretenimiento. El problema número 10 versa sobre el área de una figura parecida a una cesta, pero no está claro y resulta difícil de entender. Otro, el número 14, es considerado de particular importancia porque da un método para encontrar el volumen de un tronco de pirámide: "Sea un tronco de pirámide de 6 de altura por 4 de base y por 2 en la parte superior. Hallas el cuadrado de 4, da 16. Hallas el doble de 4, da 8. Hallas el cuadrado de 2, da 4. Sumas 16, 8 y 4, da 28. Tomas un tercio de 6, da 2. Tomas el doble de 28, da 56. Ves, es 56. Lo has calculado correctamente."

Detalle del papiro Rhind

El papiro Rhind (c. 1650 a.C.) es otro de los grandes textos matemáticos de Egipto. Fue escrito por el escriba Ahmes aproximadamente en 1650 a. C., a partir de escritos de doscientos años de antigüedad, según reivindica Ahmes al principio del texto, aunque resulta imposible saber qué partes del papiro corresponden a estos textos anteriores. Es un papiro de unos seis metros de longitud y 33 cm de anchura, en un buen estado de conservación, con escritura hierática y contenidos matemáticos: un manual de instrucciones sobre aritmética y geometría. Contiene 87 problemas matemáticos en los que aparecen fórmulas de áreas y volúmenes, progresiones, repartos proporcionales, reglas de tres, trigonometría básica. También encontramos como trabajar con fracciones unitarias (las inversas de los números naturales: 1/n), numeros primos y compuestos; media aritmética, geométrica y armónica; interpretaciones sencillas de la Criba de Eratóstenes y de la teoría del número perfecto (del número 6). Muestra la forma de resolver ecuaciones lineales de primer grado, así como las serie aritméticas y geométricas. Además, tres elementos geométricos que figuran en el papiro Rhind sugieren el más simple de los fundamentos de la geometría analítica: