Las matemáticas en el siglo XVIII
De Wikipedia
<<< Historia de las Matemáticas
Como hemos visto, el conocimiento de los números naturales, 1, 2, 3 ,..., que aparece en las estructuras monolíticas, es más antiguo que cualquier texto escrito que se conserve. Las primeras civilizaciones - en Mesopotamia, Egipto, India y China - sabían aritmética.
Una forma de ver el desarrollo de los distintos sistemas de numeración de la matemática moderna, es ver los nuevos números estudiados e investigados para responder a preguntas sobre aritmética sbre números mas antiguos. En tiempos prehistóricos, las fracciones daban respuesta a la pregunta: ¿qué número, multiplicado por 3, da 1? En la India y China, y mucho más tarde en Alemania, los números negativos se desarrollaron para responder a la pregunta: ¿qué obtienes cuando se resta un número mayor a otro menor?
Otra pregunta natural es: ¿qué tipo de número es la raíz cuadrada de dos? Los griegos sabían que no era una fracción, y esta cuestión puede haber desempeñado un papel en el desarrollo de la fracción continua. Sin embargo, una mejor respuesta vino con la invención de los decimales, desarrollados por John Neper (1550-1617) y perfeccionados más tarde por Simon Stevin. Usando decimales, y una idea que anticipa el concepto de límite, Neper estudió una nueva constante, que Leonard Euler (1707-1783) llamó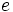 
Euler fue muy influyente en la normalización de otros términos matemáticos y notaciones. El nombró a la raíz cuadrada de menos 1 con el símbolo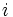 
(unidad imaginaria). También popularizó el uso de la letra griega π al enunciar la razón entre la circunferencia de un círculo y su diámetro. Posteriormente, obtuvo una de las más notables identidades de las matemáticas, la identidad de Euler.
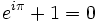
Hacia finales del siglo XVIII, Lagrange iniciaría una rigurosa teoría de funciones y de la mecánica. Ese periodo vio la gran obra de Laplace sobre mecánica celeste así como grandes progresos de Monge y Carnot en la geometría sintética.
Videos
Euler, el genio más prolífico (22´) Sinopsis: Euler es un matemático entrañable, y no sólo por sus trabajos. A lo largo del siglo XVIII ensanchó las fronteras del conocimiento matemático en todos sus campos. Sus obras completas, Opera Omnia, ocupan más de 87 grandes volúmenes, y la importancia de sus descubrimientos nos hacen dudar a veces que puedan ser obra de una sola persona. Aunque Euler no era una persona normal: era un genio.A los 19 años ganó el premio de la Academia de Ciencias de Francia por un trabajo sobre la mejor ubicación de los mástiles de los barcos. Esto no es sorprendente, salvo por el hecho de que Euler nació en Basilea ( Suiza) y no había visto un barco en su vida. Volvería a ganar otros once premios de la Academia. Euler recogió el guante de todos los retos planteados por Fermat y dio respuesta satisfactoria a todos menos uno, el último teorema. Hoy su nombre está asociado a resultados de casi todas las ramas de las matemáticas: análisis, álgebra, teoría de números, series, geometría, astronomía… Lo más sorprendente es que Euler escribió más de la mitad de su obra completamente ciego realizando sus cálculo mentalmente. Nada extraño para alguien que era capaz de recitar la Eneida completa y en latín.
Un número llamado e (13') Sinopsis: Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿ Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e.
Las matemáticas en la revolución francesa (20´) Sinopsis: En 1791, haciendo un alto en sus disputas políticas, la Asamblea Nacional Francesa define lo que con los años se convertirá en la medida de longitud universal: el metro. La diezmillonésima parte del cuadrante del meridiano terrestre. Gracias a los matemáticos franceses hoy compramos en kilos y viajamos kilómetros.Una pléyade de notables matemáticos como nunca antes habían convivido en Francia, va a vivir de forma intensa los acontecimientos de la Revolución Francesa: Joseph Louis Lagrange, Gaspard Monge, Peirre Simon de Laplace, Adrien Marie Legendre, y el marqués de Condorcet, van a llevar a la matemática francesa a su más alta cima. Ellos van a poner los fundamentos científicos del Análisis, del cálculo de probabilidades, de la Geometría descriptiva y de la Astronomía moderna. Pero van a hacer algo más: van a crear el modelo de la moderna enseñanza de las matemáticas superiores, un modelo que pervivirá más de dos siglos. 14 de julio, fiesta nacional francesa. Los franceses celebran el nacimiento del Estado moderno. El resto del mundo deberíamos celebrar con ellos algo quizás más importante: uno de los momentos más brillantes de la Ciencia Moderna.
