Método de reducción al absurdo
De Wikipedia
En latín, "Reductio ad absurdum", es un método lógico de demostración.
Para demostrar la validez de una proposición, se supone que la tesis de la proposición a demostrar es falsa, y mediante una concatenación de inferencias lógicas válidas se deriva una contradicción lógica, un absurdo. Así se concluye que la hipótesis de partida (la negación de la tesis) ha de ser falsa, y que la proposición es válida.
A este método también se le conoce como prueba por contradicción o prueba ad absurdum. Parte de la base es el cumplimiento del principio de exclusión de intermedios: "una proposición que no puede ser falsa es necesariamente verdadera, y una proposición que no puede ser verdadera es necesariamente falsa".
Considérese la proposición: "No existe un número racional mínimo mayor que cero".
En una reducción al absurdo se comenzaría por asumir lo contrario, es decir, supongamos que existe un racional mínimo mayor que cero: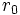 
.
Ahora consideremos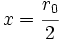 
. Se trata de un número racional mayor que cero, y menor que 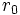. Eso es absurdo, pues contradice la hipótesis de partida de que 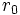era el número racional mínimo mayor que cero. Por lo tanto se debe concluir que la proposición asumida como cierta, «hay un número racional mínimo mayor que cero», es falsa.
