Mínimo común múltiplo (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 20)
Mínimo común múltiplo
El mínimo común múltiplo (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números, distinto de cero.
Propiedad
- Si a es múltiplo de b, entonces
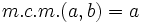 .
.
- Los múltiplos comunes de varios números son también múltiplos del m.c.m.
- Cualquier múltiplo del m.c.m. de varios números también lo es de dichos números.
- Dados varios números, si se multiplican o dividen por otro número entonces su m.c.m también queda dividido o multiplicado por el mismo número.
Cálculo del mínimo común múltiplo
Nos preguntamos a continuación por los múltiplos comunes de dos o más números? ¿Nos interesa encontrar el mayor o el menor? ¿Será útil?.
En el caso de los múltiplos, nos interesará encontrar el común más pequeño. No tiene sentido preguntarse por el mayor, pues hay infinitos múltiplos comunes a varios números. Una vez encontrado el más pequeño, se pueden conseguir tantos como quieras, sólo tienes que multiplicarlo por cualquier número natural.
Una posible estrategia sería buscar múltiplos de los números por separado hasta que lleguemos a encontrar el primero que sea igual para todos. A este procedimiento lo llamaremos 2método artesanal".
Procedimiento artesanal
Para calcular el mínimo común múltiplo de dos o más números obtendremos los múltiplos de dichos números y seleccionaremos el primero que se repita en todos ellos.
Calcula el m.c.m.(24,60) por el método artesanal:
- Múltiplos de 24: 24, 48, 72, 96, 120, 144,...
- Múltiplos de 60: 60, 120, 180, ...
- m.c.m.(24,60)= 120
Problemas prácticos en los que calcularemos el m.c.m. por el método artesanal.
1) Dados los números del 1 al 20:
- a) Rodea de rojo los múltiplos de 3 y de azul los de 6.
- b) ¿Cuáles son múltiplos comunes de 3 y 6?
- c) ¿Cuál es el m.c.m. de 3 y 6?
2) Calcula hallando los múltiplos comunes:
- a) m.c.m.(3, 5)
- b) m.c.m.(4, 5)
- c) m.c.m.(3, 7)
- d) m.c.m.(4, 6)
- e) m.c.m.(3, 9)
3) Calcula hallando los múltiplos comunes:
- a) m.c.m.(10, 20, 8)
- b) m.c.m.(2, 4, 5)
- c) m.c.m.(3, 4, 6)
Calcula m.c.m.(15, 6, 10)
Actividad en la que podrás obtener el m.c.m. de dos números por el método artesanal.
El método artesanal es lento y puede llegar a exigir escribir mucho. No es un buen método para números grandes. A continuación presentamos un método mejor, que llamaremos "método óptimo", y que se apoya en la factorización.
Sabemos que cada múltiplo de un número entero contiene a todos los factores primos de dicho número. Entonces, lo lógico sería coger todos los factores que aparezcan en las descomposiciones de los números con los que trabajemos. Lógicamente, si hay factores repetidos, los escogeremos una sola vez, ya que queremos que nuestro múltiplo común sea el menor de todos los que hay.
Procedimiento óptimo
Para obtener el m.c.m. de dos o más números se siguen los siguientes pasos:
- Se descomponen los números en factores primos.
- Se toman los factores comunes y no comunes con mayor exponente.
- Se multiplican dichos factores y el resultado obtenido es el m.c.m.
Calcula el m.c.m.(24,60) por el método óptimo:
- Descomponemos 24 y 60 en sus factores primos:
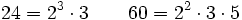
- Multiplicando todos los factores elevados al mayor exponente:
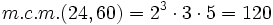
Tutorial que explica el significado del mínimo común múltiplo con un simpático ejemplo.
Tutorial que explica el significado del mínimo común múltiplo, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los múltiplos de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 06:33: ¿Qué es el Mínimo Común Múltiplo? Método de extracción de múltiplos.
- 06:33 a 11:18: Método general para calcular el MCM. Ejemplos.
Tutorial que explica qué es y cómo se calcula el mínimo común múltiplo de dos o tres números.
Mínimo común múltiplo de dos números enteros. Ejemplo.
Tutorial que explica qué es y cómo se calcula el mínimo común múltiplo de dos números. Desarrolla un ejemplo en el que calcula el m.c.m. mediante el método artesanal.
Cálcula el mínimo común múltiplo de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Cálcula el mínimo común múltiplo de:
a) 4 y 3
b) 4 y 30
c) 75, 25 y 15
d) 98, 10 y 45
Cálcula el mínimo común múltiplo de:
a) 6 y 8
b) 14, 21 y 28
Cálcula el mínimo común múltiplo de:
a) 4 y 6
b) 9, 10 y 15
Calcula el mínimo común múltiplo de 28 y 21 por el método artesanal y el método óptimo.
Calcula:
- m.c.m.(6, 8)
- m.c.m.(2, 4, 10)
- m.c.m.(10, 15)
- m.c.m.(2, 5, 30)
Calcula:
- m.c.m.(4, 10)
- m.c.m.(8, 14, 20)
Calcula: m.c.m.(72, 108).
Calcula: m.c.d.(336, 540).
Calcula: m.c.d.(12, 9, 108).
Calcula:
- a) m.c.m.(20, 2)
- b) m.c.m.(24, 18)
Calcula m.c.m.(20, 18)
- Actividad en la que podrás obtener el m.c.m. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.m. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.m. de tres números por descomposición factorial.
Actividades sobre cómo se calcula el mínimo común múltiplo.
Cálculo del mínimo común múltiplo de dos números
Ejercicios de cálculo del mínimo común múltiplo de dos números
Ejercicios de autoevaluación sobre el m.c.m.
Problemas
Problema resuelto: m.c.m.
Un distribuidor de electrodomésticos desea cargar dos palés, uno con lavavajillas de 45 kg y otro con frigoríficos de 40 kg, de forma que ambos pesen lo mismo y lo menos posible. ¿Cuánto pesará cada palé?
Solución: 360 Kg
María tarda 6 min en dar una vuelta al barrio corriendo y Pedro 8 min. ¿Cuándo coincidirán de nuevo en la plaza si han salido juntos de ella a las 10:15?
Un viajero va a Brasil cada 18 días y otro cada 24. Si hoy han estado los dos en Brasil, ¿cuántos días pasarán para que vuelvan a coincidir?
Necesitamos hacer bolsitas con 3 caramelos de los colores de las luces de un semáforo (rojo, verde y amarillo). En la tienda donde venden los caramelos me dicen que los caramelos rojos vienen en paquetes de 6, los amarillos en paquetes de 5 y los verdes en paquetes de 10. ¿Cuántos paquetes, como mínimo, tenemos que usar para hacer bolsitas con cada uno de los tres colores sin que nos sobre ninguno?.¿Cuántas bolsitas nos saldrán?
Cuatro ciclistas compiten en una pista circular y la recorren totalmente en 8, 10, 12 y 15 segundos, respectivamente. Si parten juntos, ¿en cuantos minutos se encontraran en la partida?
A) 120; B) 1; C) 2; D) 3
De los 630 primeros números enteros positivos, ¿cuántos son múltiplos de 3 y 7 a la vez?
A) 10; B) 21; C) 20; D) 30
El número de páginas de un libro está comprendido entre 300 y 350. Si se cuentan de 3 en 3, sobran 2; de 4 en 4 sobran 3 y de 7 en 7 sobran 6. ¿Cuántas páginas tiene el libro?
A) 325; B) 345; C) 315; D) 335
Claudia va al hospital cada 15 días, Joaquín cada 12 y Ángel cada 18. Si hoy es 05 de Septiembre y se encontraron en el hospital, entonces la fecha más próxima en la cual se encontrarán los tres nuevamente será:
A) 5 de Enero; B) 5 de Diciembre; C) 4 de Marzo; D) 4 de Febrero; E) 2 de Marzo
Antonio va al piscina cada 6 días y Alba cada 4 días. ¿Cuántos días, pasarán para que vuelvan a coincidir por primera vez? ¿Qué día de la semana será?
Nivel más avanzado:
Se compran televisores de 17 pulgadas a 3 por 1200 dólares y se venden a 4 por 2400 dólares. Para ganar 3000 dólares, ¿cuántos se debe vender?
A) 12; B) 15; C) 14; D) 8; E) 10
Un vendedor tiene entre 600 y 800 naranjas. Si se puede agruparlas de 15 en 15, de 18 en 18 y de 24 en 24 sin que sobre alguna, ¿cuántas naranjas tiene el vendedor?
A) 640; B) 6800; C) 720; D) 760; E) 800
Se tiene tres reglas calibradas, de 48 cm cada una. La primera está calibrada con divisiones de 4/21 cm; la segunda, con divisiones de 24/35 cm; y la tercera, con divisiones de 8/7 cm. Si se hace coincidir las tres reglas en sus extremos de calibración, ¿cuántas coincidencias de calibración hay en las tres reglas?
A) 13; B) 14; C) 4; D) 15; E) 12
Marina tiene una planta que riega cada 3 días y otra que riega cada 5. Si el lunes ha regado las dos, ¿qué día de la semana volverá a regar otra vez las dos?
En una parada de autobús comienzan dos líneas. Los autobuses de una línea salen cada 6 minutos, y los de la otra, cada 8. Si dos autobuses de distintas líneas salen a la misma hora, ¿Cuántos minutos tardarán en volver a coincidir en la salida?
Un faro se enciende cada 12 segundos, otro cada 18 segundos, y un tercero cada minuto. A las 6:30 de la tarde los tres coinciden. Averigua las veces que volverán a coincidir durante los próximos 5 minutos.
Tres ciclistas tardan en dar la vuelta a un velódromo 48, 56 y 72 segundos, respectivamente. Si salen a la vez, ¿al cabo de cuántos segundos volverán a coincidir en la salida?
Ejercicios propuestos
|
Ejercicios propuestos: Mínimo común múltiplo |

