Magnitudes directamente proporcionales (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 91)
Relación de proporcionalidad directa
Actividad Descripción: Cálculo del valor de varios a partir del valor de uno
Dos magnitudes son directamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda multiplicada (resp. dividida) por el mismo número.
Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar (resp. disminuir) una de ellas, aumenta (resp. disminuye) la otra. No es exactamente así. No es suficiente con que aumente (resp. disminuya) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se multiplica (resp. divide) la otra, por el mismo número.
La capacidad de un depósito de agua y el tiempo que tarda en llenarse son magnitudes directamente proporcionales, ya que si el depósito tiene el doble (o el triple,...) de capacidad, el tiempo que tarda en llenarse es el doble (o el triple,...).
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
Tutorial 1 (1'00") Sinopsis: Magnitudes directamente proporcionales. Ejemplo.
Tutorial 2 (4'16") Sinopsis:Magnitudes directamente proporcionales. Ejemplos.
Tutorial 3 (4'31") Sinopsis: Relaciones directamente proporcionales. Ejemplo.
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Ejercicio 1 (3'01") Sinopsis: Hoy Nate tiene 100 plátanos. Él va a comer 2 plátanos de ellos cada día.
- a) ¿El número de plátanos que Nate deja sin comer es directamente proporcional al número de días transcurridos?
- b) ¿Y el número de plátanos que come cada día?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Ejercicio 2 (1'56") Sinopsis: Un cine cobra $10.50 por boleto y $5 por bolsa de palomitas. Tú nunca compras las palomitas porque te parece que son muy caras. ¿El precio total de lo que pagas es directamente proporcional al número de boletos que compras?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Magnitudes directamente proporcionales Descripción: Actividades para aprender que son magnitudes directamente proporcionales.
Actividad 1 Descripción: Actividades sobre magnitudes directamente proporcionales.
Actividad 2 Descripción: Completa las tablas de manera que las magnitudes sean directamente proporcionales.
Actividad 3 Descripción: Actividades sobre magnitudes directamente proporcionales.
Autoevaluación 1 Descripción: Actividad sobre magnitudes directamente proporcionales.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Autoevaluación 3 Descripción: Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Constante de proporcionalidad directa
Al dividir dos magnitudes directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama constante o razón de proporcionalidad.
En el ejemplo anterior, en el que relacionabamos la capacidad de un depósito con el tiempo que tardaba en llenarse
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
se observa que:
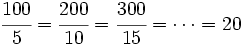
La constante de proporcinalidad es 20.
Constante de proporcionalidad directa (0'44") Sinopsis: Razón de proporcionalidad directa. Ejemplo.
Constante de proporcionalidad directa (I) Descripción: Actividades para aprender a calcular la constante de proporcionalidad directa.
Constante de proporcionalidad directa (II) Descripción: Actividades para aprender a calcular la constante de proporcionalidad directa.
Ejercicio Descripción: Halla la constante de proporcionalidad.
(Pág. 91)
Método de reducción a la unidad
Método de reducción a la unidad
Dadas dos magnitudes directamente proporcionales, el método de reducción a la unidad consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). Ese valor obtenido es la constante de proporcionalidad. A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que multiplicar la primera magnitud por dicha constante.
Compramos 4 kg de plátanos por 6 €. ¿Cuánto costarán 7 kg?
Solución:
Primero averiguamos lo que cuesta 1 kg (la unidad):
Peso (kg) Coste (€)
---------- ----------
4 --------> 6
1 --------> x
€
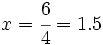A partir del precio de 1 kg es fácil sacar el precio 7 kg:
Peso (kg) Coste (€)
---------- ----------
1 --------> 1.5
7 --------> x
€
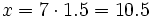Método de reducción a la unidad (3'59") Sinopsis:Ejemplo de reducción a la unidad con magnitudes directamente proporcionales.
Actividad 1 Descripción: Actividad para aprender el método de reducción a la unidad.
Actividad 2 Descripción: Actividad para aprender el método de reducción a la unidad.
Actividad 3 Descripción: Actividad para aprender el método de reducción a la unidad.
Ejercicios propuestos
 Ejercicios propuestos: Relación de proporcionalidad directa (Pág. 91)
|
(Pág. 92)
Regla de tres directa
Procedimiento
La regla de tres directa es un método que se apoya en el hecho de que al dividir dos magnitudes directamente proporcionales el cociente no varía. Esto permite establecer una igualdad entre dos fracciones, de la cual se despeja el valor desconocido.
Compramos 4 kg de plátanos por 6 €. ¿Cuánto costarán 7 kg?
Solución:
Peso (kg) Coste (€)
---------- ----------
4 --------> 6
7 --------> x
€
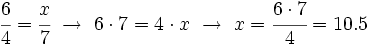Problema 1 (1'32") Sinopsis: Una paleta de jamón de 4 kg cuesta40 €. ¿Cuánto costará otra paleta de igual calidad de 5 kg?
Problema 2 (2'43") Sinopsis:En un día de trabajo de 8 horas, un obrero ha hecho 10 cajas. ¿Cuántas horas tardará en hacer 25 cajas similares?
Regla de tres simple directa (I) Descripción: Actividades para aprender y practicar la regla de tres simple directa.
Regla de tres simple directa (II) Descripción: Actividades para aprender y practicar la regla de tres simple directa.
Problema 1 Descripción: Por 3 horas trabajando he ganado 60 €. ¿Cuánto ganaré por 8 horas?
Problema 2 Descripción: 600 gramos de queso cuestan 12 €. ¿Cuánto gramos podré comprar con 4.50 €?
Test: Problemas Descripción: Problemas de regla de tres.
Actividades y videotutoriales
Tutorial 1 (15'51") Sinopsis:Tutorial que explica los problemas de proporcionalidad directa, viendo los métodos de igualdad de cocientes, método general, reducción a la unidad y regla de tres directa.
Tutorial 2 (7'05") Sinopsis:Problemas de proporcionalidad directa:
- Me han dado 4.20 € como paga de los últimos 7 días. ¿Cuánto me darán por 15 días?
- A una fábrica de muebles han llegado 840 camiones de madera en 60 días. Si el flujo de camiones se mantiene, ¿cuántos camiones recibirá en un año?
- Hemos tardado 2 horas y media en recorrer un trayecto de 125 km. Si seguimos a la misma velocidad constante, ¿cuánto tiempo tardaremos si la ruta de regreso es de 225 km?
Tutorial 3 (6'04") Sinopsis:Tutorial que explica el concepto de magnitudes directamente proporcionales.
Tutorial 4 (6'04") Sinopsis:Tutorial que explica los problemas de proporcionalidad directa.
Problema 1 (3'02") Sinopsis: Se necesitan 70 galones de pintura para embellecer 5 casas de un condominio. ¿Que cantidad de pintura se requiere para 12 casas similares?
Problema 2 (2'31") Sinopsis: Si una máquina copiadora tarda 8 segundos en sacar 20 copias, ¿cuánto tiempo tardará en sacar 45 copias?
Problema 3 (5'32") Sinopsis: Plantea la proporción sin resolverla:
- a) 9 marcadores cuestan $115. ¿Cuánto cuestan 7 marcadores?
- b) 7 manzanas cuestan %50. ¿Cuántas manzanas puedo comprar por $80?
- c) Una receta de pastel para 5 personas requiere 2 huevos. ¿Cuántos huevos requiere la misma receta para 15 personas?
Problema 4 (6'03") Sinopsis: Mica puede comer 21 tacos en 66 minutos. Ella quiere saber cuántos minutos tardará en comer 35 tacos si puede mantener el mismo ritmo.
Problema 5 (5'49") Sinopsis: Una receta para galletas de avena contiene 2 tazas de harina por cada 3 tazas de avena. ¿Cuánta harina se necesita para elaborar una gran cantidad de galletas que requieren 9 tazas de avena?
Problema 6 (4'05") Sinopsis: Tu carro puede recorrer 25 millas por galón de combustible, y quieres hacer un viaje de 400 millas. Justo ahora la gasolina cuesta 30 pesos por galón. ¿Cuánto te va a acostar la gasolina para el vaije?
Problemas 1 Descripción: Practica distintos problemas de proporcionalidad directa.
Problemas 2 Descripción: Practica distintos problemas de proporcionalidad directa.
Problemas 3 (guiados) Descripción: Problemas 4 Descripción: Problemas de regla de tres simple directa con pistas.
Actividad Descripción: Tasas.
Autoevaluación 1 Descripción: Actividades para practicar la regla de tres simple directa.
Autoevaluación 2 Descripción: Actividades para practicar la regla de tres simple directa.
Autoevaluación 3 Descripción: Actividades para practicar la regla de tres simple directa.
Autoevaluación 4 Descripción: Escribir proporciones.
Autoevaluación 5 Descripción: Problemas verbales de proporciones.
Autoevaluación 6 Descripción: Problemas verbales de varias unidades.
Autoevaluación 7 Descripción: Problemas de autoevaluación sobre la regla de tres simple directa.
Autoevaluación 8 Descripción: Ejercicios y problemas de autoevaluación sobre proporcionalidad directa.
Autoevaluación 9 Descripción: Tasas unitarias.
Autoevaluación 10 Descripción: Problemas de tasas.
Autoevaluación 11 Descripción: Comparar tasas.
Ejercicios propuestos
Ejercicios propuestos: Relación de proporcionalidad directa (Pág. 93)
|
