Números naturales
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | Tablas de multiplicar | WIRIS Geogebra Calculadora |
Tabla de contenidos
|
Números naturales
El conjunto de los números naturales es:
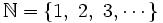
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Representación de los números naturales
Representación de los números naturales
Orden en los números naturales
En la representación de los números naturales en la recta numérica se observa la relación de orden que existe en dicho conjunto. Diremos que los números naturales están ordenados (véase números ordinales), lo que nos permite comparar dos números naturales entre sí.
Un número natural es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Orden en el conjunto de los números naturales
Dados dos números naturales cualesquiera,  y
y  , se dará uno de los siguientes casos:
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
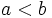 (Se lee "a es menor que b").
(Se lee "a es menor que b").
- El primero es igual que el segundo:
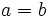 (Se lee "a es igual que b").
(Se lee "a es igual que b").
- El primero es mayor que el segundo:
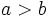 (Se lee "a es mayor que b").
(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
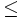 )
)
- Mayor o igual que (
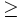 )
)
- Distinto (
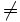 )
)
Comparación de números naturales.
Orden y comparación de números naturales.
Igualdad y desigualdad de números naturales. Simbología. Ejemplos.
Completa el hueco con el signo "mayor que" (>), "menor que" (<) o "igual" (=):
- siete millares + nueve centenas + siete unidades ___ 7000 + 970
¿Cuál es el menor número con 5 cifras? (los ceros a la izquierda no cuentan)
¿Cuál es el mayor número de 6 cifras?
Escribe el mayor número posible con las cifras 3, 5, 2, 8, 9 y 6.
Compara números de 2 dígitos.
Notación desarrollada de un número natural
La notación desarrollada de un número natural consiste en expresarlo como suma de los valores relativos de cada uno de sus dígitos.
Notación desarrollada de números naturales.
Notación desarrollada.
Ejemplos de notación desarrollada de un número natural
Escribe en notación desarrollada los números:
a) 385
b) 1834
Escribe en notación desarrollada los números:
a) 672
b) 4521
Escribe en notación desarrollada los números:
a) 23 772
b) 127 050
Escribe en notación desarrollada el número 14 897.
Lectura y escritura de números naturales
Reglas
- Al leer números, primero se separan las cifras, de tres en tres, empezando por la derecha. Después se leen de izquierda a derecha, como si fuesen números de tres cifras, y se añaden las palabras mil, millones, billones, trillones,... donde corresponda.
- Hasta el número treinta siempre se escribe con una sola palabra.
- Según indica la Real Academia Española, al escribir números de más de cuatro cifras, se agruparán estas de tres en tres, empezando por la derecha, y separando los grupos por espacios en blanco y no por puntos o comas (8 327 451). Los números de cuatro cifras se escriben sin espacios de separación (2458).
Lectura y escritura de números naturales
Escribe cómo se lee el número 3 454 783 215 571 247 869 523
Escribe cómo se leen los números:
- a) 12 529 345 897 883 143
- b) 1 450 937 845 967 388 492 123
Escribe el número "seiscientos cuarenta y cinco millones, quinientos ochenta y cuatro mil, cuatrocientos sesenta y dos".
Practica la lectura y escritura de números naturales.
Autoevaluación sobre lectura y escritura de números naturales y sobre cómo expresarlos en forma desarrollada.
Los números grandes
Los números naturales son infinitos y nuestro sistema de numeración decimal nos permite representar cualquiera de ellos por muy grandes que sean.
Los números grandes más usuales son:
- 1 millón = 1 000 000 (1 seguido de 6 ceros)
- 1 billón = 1 millón de millones = 1 000 000 000 000 (1 seguido de 12 ceros)
- 1 trillón = 1 millón de billones = 1 000 000 000 000 000 000 (1 seguido de 18 ceros)
- 1 millardo = Mil millones = 1 000 000 000 (1 seguido de 9 ceros)
Exposición interactiva de la representación de números grandes en el sistema de numeración decimal.
Desde el millón hasta el quintillón.
¿Hasta qué número es posible contar? ¿Hay un número mayor que todos, o la cuenta no acaba nunca y es infinita? ¿Cuál es el número más grande que alguien haya podido imaginar? Errata en minuto 1:05 -> en realidad ese número se lee "setenta mil trillones" en español y en inglés si sería "seventy sextillion" por lo que hay un error en el vídeo.
Aunque parezca que los grandes números son muy modernos, no es así en absoluto. En la Universidad de Oxford se conserva una pieza egipcia de unos 5000 años de antigüedad que registra la victoria del rey Narmer sobre los libaneses al oeste del delta del Nilo; en ella se describe que Egipto se cobró 120 000 prisioneros, 400 000 bueyes y 1 422 000 cabras. Los centenares de miles y los millones también se hallan mencionados en el egipcio "Libro de los muertos".
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 12)"
Operaciones con naturales
- Sabrías sumar de forma fácil y sin calculadora los 100 primeros números naturales?
- El misterioso número 6174.
Suma y resta de números naturales
Videotutorial que resume lo que vamos a ver en este apartado sobre la suma y resta de números naturales y sus propiedades.
Practica con las operaciones de suma y resta de números naturales y con sus propiedades.
Suma
- Sumar es unir, juntar, añadir.
- La suma o adición de dos números naturales, a y b, da como resultado otro número natural, c. Se representa: a+b=c.
- a y b reciben el nombre de sumandos.
- El resultado, c, se denomina suma.
El concepto de adición o suma en el conjunto de los números naturales.
El concepto de adición o suma en el conjunto de los números naturales.
Calcula:
a) 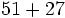
b) 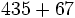
c) 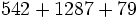
d) 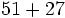
Calcula: 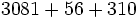
Calcula: 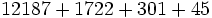
Calcula: 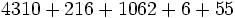
Cálculo mental con sumas.
Propiedades de la suma de números naturales
Propiedades de la suma
- Operación interna: el resultado de sumar dos números naturales es otro número natural.
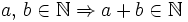
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
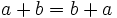
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
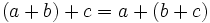
- Elemento neutro: El elemento neutro para la suma es el 0.
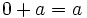
Propiedades de la suma de números naturales. Ejemplos.
Propiedades de la suma de números naturales. Ejemplos.
Propiedades conmutativa y asociativa de la suma de números naturales. Ejemplos.
El elemento neutro de la suma y del producto de números naturales. Ejemplos.
A look behind the fundamental properties of the most basic arithmetic operation, addition.
(Disponibles los subtítulos en inglés)
Aplicación de las propiedades asociativa y conmutativa de la suma. Ejemplos.
Usa la propiedad conmutativa de la suma para escribir la expresión 5 + 8 + 5 de una manera diferente. Comprueba que ambas expresiones dan el mismo resultado.
Usa la propiedad asociativa de la suma para escribir la expresión (77 + 2) + 2 de una manera diferente. Comprueba que ambas expresiones dan el mismo resultado.
Propiedades de la suma de números naturales.
Propiedades de la suma de números naturales.
Resta
- Restar es quitar, hallar lo que falta o lo que sobra, es decir, calcular la diferencia.
- La resta o sustracción de dos números naturales, a y b, se representa: a-b=c
- a es el minuendo, b el sustraendo y c la diferencia.
La resta de números naturales no cumple las propiedades de la suma:
- No es operación interna:
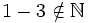 .
.
- No cumple la propiedad conmutativa:
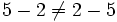
- No cumple la propiedad asociativa:
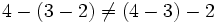
El concepto de sustracción en el conjunto de los números naturales.
Repaso de primaria sobre resta de números naturales.
Calcula:
a) 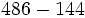
b) 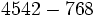
Calcula: 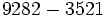
Calcula: 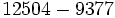
Calcula: 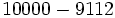
Cálculo mental con restas.
Ejercicios de autoevaluación sobre la resta de números naturales.
Multiplicación o producto de números naturales
Multiplicar es una forma abreviada de realizar una suma de sumandos iguales.
Videotutorial que resume lo que vamos a ver en este apartado sobre la multiplicación de números naturales y sus propiedades.
- Multiplicar dos números naturales consiste en sumar uno de los factores consigo mismo tantas veces como indica el otro factor.
- La multiplicación o producto de dos números naturales,
 y
y  , se representa
, se representa 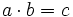 .
.
 y
y  se llaman factores y c se denomina producto.
se llaman factores y c se denomina producto.
El concepto de multiplicación en el conjunto de los números naturales.
Calcula:
a) 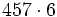
b) 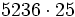
Calcula: 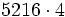
Calcula: 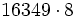
Calcula: 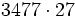
Calcula: 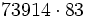
Calcula: 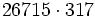
Calcula: 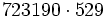
Cálculo mental con multiplicaciones.
Para construir con palillos una fila de cuatro cuadrados contiguos se necesitan 13 palillos. ¿Cuántos palillos se necesitarán para construir una fila de 26 cuadrados contiguos?
Si 8 máquinas producen 1500 piezas, ¿cuántas piezas fabricarán 40 máquinas del mismo tipo?
Propiedades de la multiplicación de números naturales
Propiedades de la multiplicación
- Operación interna: El producto de dos números naturales es otro número natural:
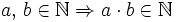
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
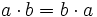
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
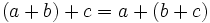
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
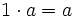
Propiedades conmutativa y asociativa del producto de números naturales. Ejemplos.
Propiedad distributiva de los números naturales. Ejemplos.
El elemento neutro de la suma y del producto de números naturales. Ejemplos.
Ejemplos de uso de la propiedad distributiva y de cómo se saca factor común.
Propiedad asociativa y conmutativa de forma visual.
Propiedad distributiva de forma visual.
Más formas de pensar en la multiplicación. Multiplicando usando la propiedad asociativa.
Otra forma de multiplicar usando la propiedad distributiva.
El elemento neutro de la multiplicación de números naturales es el 1.
The commutative property is common to the operations of both addition and multiplication and is an important property of many mathematical systems.
(Disponibles los subtítulos en inglés)
A look at the logic behind the associative and distributive properties of multiplication.
(Disponibles los subtítulos en inglés)
Usa la propiedad conmutativa de la multiplicación para multiplicar 2 · 34 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad asociativa de la multiplicación para multiplicar (12 · 3) · 10 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad distributiva de la multiplicación sobre la suma para calcular 4·(8 + 3).
Usa la propiedad distributiva de la multiplicación sobre la resta para calcular 5·(9 - 4).
Usa la propiedad distributiva de la multiplicación sobre la suma para sacar factor común en las siguientes expresiones:
- a) 20 + 30
- b) 90 + 27
- c) 55 + 35
- d) 12 + 75
Multiplica 6 · 7981 usando la propiedad distributiva.
Multiplica 78 · 65 usando la propiedad distributiva.
Propiedad conmutativa:
Introducción a la propiedad conmutativa del producto de números naturales.
Resumen de la propiedad conmutativa del producto de números naturales.
Propiedad conmutativa del producto de números naturales.
Propiedad asociativa:
Introducción a la propiedad asociativa del producto de números naturales.
Resumen de la propiedad asociativa del producto de números naturales.
Propiedad asociativa del producto de números naturales.
Propiedad distributiva:
Introducción a la propiedad distributiva del producto sobre la suma de números naturales.
Resumen de la propiedad distributiva del producto sobre la suma de números naturales.
Propiedad distributiva del producto sobre la suma de números naturales.
Saca factor común usando la propiedad distributiva del producto sobre la suma de números naturales.
Propiedades de la multiplicación:
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Ejemplo: Propiedad distributiva del producto
Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
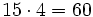
- Teresa------>
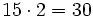
- Total--------->
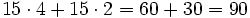 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
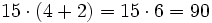 €
€
Producto por 10, 100, 1000, ....
Para multiplicar un número por la unidad seguida de ceros (10, 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).
Multiplicar números de 1 dígito por 10, 100 y 1000.
Multiplicando números de 1 dígito por múltiplos de 10.
Multiplicar números de 1 dígito por múltiplos de 10, 100 y 1000.
Multiplicando dos múltiplos de 10.
Multiplica números de 1 dígito por 10, 100 y 1000.
Multiplica por decenas.
Multiplica dos múltiplos de 10.
Multiplica números de 1 dígito por un múltiplo de 10, 100 y 1000
División o cociente de números naturales
El siguiente video resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Videotutorial que resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
El concepto de división exacta en el conjunto de los números naturales.
División exacta y entera de números naturales. Algoritmo de la división. Ejemplos.
Repaso sobre divisiones de números naturales por 1 o 2 cifras.
Aprende a dividir por una cifra
Aprende a dividir por dos cifras
Ejercicios de divisiones por 1, 2 o 3 cifras.
En esta actividad podrás comprobar si una división dada es exacta o no.
Cálculo con divisiones.
En una división con resto 24, ¿cuál es el valor mínimo del divisor?
Ejercicios de autoevaluación sobre la división de números naturales y sus propiedades.
|
Actividad: Cociente y resto Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Ejercicio: División con naturales
Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división) |
Cociente por defecto y por exceso
Ejemplo: Cociente por defecto y por exceso
Un autobús con 43 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.
- a) ¿Cuántos taxis completarán?
- b) ¿Cuántos taxis se necesitan?
- c) ¿cuál es el cociente por defecto y por exceso?
a) Completan 10 taxis y sobran 3 turistas. (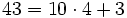 )
)
b) Se necesitan 11 taxis, aunque en el último taxi quede un asiento libre.
Propiedades de la división de números naturales
Propiedades
- No es una operación interna: La división de de números naturales no siempre es un número natural
- La división no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
- Si dividimos 0 por cualquier número distinto de 0, el resultado es 0.
- Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número.
Veamos ejemplos que ilustren estas propiedades:
- La división de números naturales no es una operación interna:
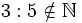
- La división de números naturales no cumple la propiedad conmutativa:
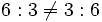
- La división de números naturales no cumple la propiedad asociativa:
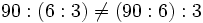
- La división de números naturales no cumple la propiedad distributiva:
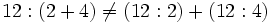
- Si dividimos 0 por cualquier número distinto de 0, el resultado es 0.:
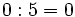
Para la última propiedad veremos un ejemplo:
Hagamos la división 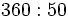
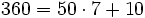 (Cociente=7; Resto=10)
(Cociente=7; Resto=10)Ahora dividimos el dividendo y el divisor por 10:
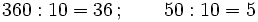
y volvemos a hacer la división:
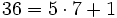 (Cociente=7; Resto=1)
(Cociente=7; Resto=1)Potenciación de naturales
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
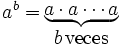 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
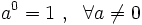 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
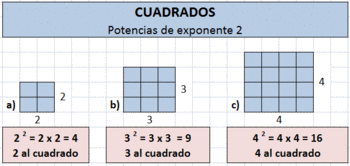
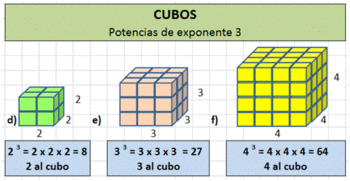
Cómo se leen las potencias:
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
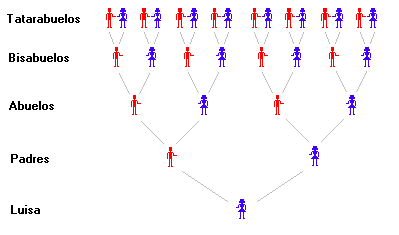
Luisa quiere saber cuántos bisabuelos y tatarabuelos ha tenido. Para contarlos dibuja en su cuaderno su árbol genealógico:
Ella tiene 2 padres (un padre y una madre): 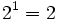 padres.
padres.
Cada uno de ellos tiene 2 padres. Por tanto, ella tiene  abuelos.
abuelos.
Cada abuelo tiene a su vez 2 padres, luego ella tiene 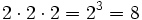 bisabuelos.
bisabuelos.
Cada bisabuelo tiene a su vez 2 padres; ella tiene 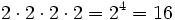 tatarabuelos.
tatarabuelos.
Potencias de números naturales con exponente natural.
Potencias de números naturales con exponente natural.
Potencias de números naturales con exponente natural. Ejemplos.
Potencias de números naturales con exponente natural. Ejemplos.
Potencias de números naturales con exponente natural. Ejemplos
Potencias de números naturales con exponente cero. Ejemplos
Potencias de números naturales. Ejemplos
Potencias de números naturales con exponente natural. Ejemplos.
Practica con las potencias de números naturales.
Introducción a las potencias.
Elevar números al cuadrado.
Repaso de potencias.
Observa cómo varía el resultado al modificar la base y el exponente.
Actividades:
Haz uso de la escena anterior y contesta en tu cuaderno:
- ¿Qué valor tiene una las potencia cuya base es el número 0, sea cual sea el exponente?
- ¿Qué valor tiene una potencia cuya base es el número 1, sea cual sea el exponente?
- ¿Qué valor tiene una potencia cuyo exponente es el número 1, sea cual sea la base?
- Calcula 100, 101, 102, 103, 104.
- Las potencias de exponente 2 se llaman cuadrados perfectos. Calcula los cuadrados de los primeros 15 números naturales.
- Las potencias de exponente 3 se llaman cubos perfectos. Calcula los cubos de los primeros 15 números naturales.
Potencias de números naturales (I)
Potencias (básico)
Potencias
Elementos de una potencia:
Rellena todas las cajas inferiores y pulsa "intro" al final. Cuando hayas marcado correctamente los tres aparecerá el mensaje CORRECTO, pero si marcas antes un número equivocado ya no aparecerá ese mensaje, por eso, no emplees los triángulos arriba y abajo para variar el número.
Expresa productos de números como potencias.
- Asocia los resultados de estas potencias:
Rellena todas las cajas inferiores y pulsa "intro" al final. Cuando hayas marcado correctamente los tres aparecerá el mensaje CORRECTO, pero si marcas antes un número equivocado ya no aparecerá ese mensaje, por eso, no emplees los triángulos arriba y abajo para variar el número.
Ana tiene 5 cajas de bombones. cada caja tiene 5 filas de bombones y cada fila tiene 5 bombones. ¿Cuántos bombones tiene Ana en total?
|
Calculadora: Potencias |
Operaciones con potencias de naturales. Propiedades
En este videotutorial haremos una introducción a las operaciones con potencias más usuales.
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
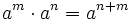
- 2. Cociente de potencias de la misma base:
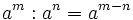
- 3. Potencia de un producto:
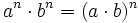
- 4. Potencia de un cociente:
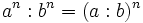
- 5. Potencia de otra potencia:
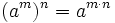
- Producto de potencias de la misma base:
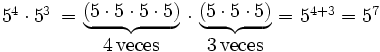
- Cociente de potencias de la misma base:
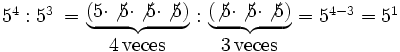
- Potencia de un producto:
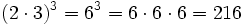
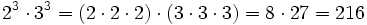
- Potencia de un cociente:
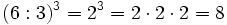
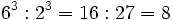
- Potencia de otra potencia:
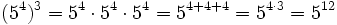
- Potencia cero: Cuando se vio la definición de potencia, dijimos que
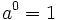 por convenio. Expliquemos ésto ahora un poco mejor:
por convenio. Expliquemos ésto ahora un poco mejor:
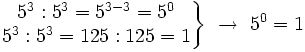
Potencias de números naturales con exponente natural.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
- Potencia de otra potencia.
- Ejemplos.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de otra potencia.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de un producto.
Aprende a calcular la potencia de un cociente.
Aprende a calcular la potencia de una potencia.
Enunciados de las propiedades de las potencias de números naturales.
Ejemplos de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Actividades
Potencias de 10
Potencia de base 10
Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente
Esto permite expresar números grandes con muchos ceros como producto de un número por una potencia de 10.
Potencias de 10.
Números naturales expresados como potencias de 10.
Escribe potencias de 10 en forma de número con todas sus cifras.
Expresa cantidades mediante potencias de base 10.
Descomposición polinómica de un número
La descomposición polinómica de un número consiste en expresar dicho número como una suma, en la que cada sumando es cada cifra del número multiplicada por una potencia de 10, cuyo exponente es una unidad menos de la posición que ocupa la cifra que la multiplica.
Actividades para aprender a hallar la descomposición polinómica de un número.
Descomposición polinómica de un número natural. Ejemplos.
Obtén la descomposición polinómica de los siguientes números naturales:
a) 928 b) 5400 c) 208 563 d) 86 324 642
Raíz cuadrada de un número natural
La raíz cuadrada es la operación inversa de elevar al cuadrado:
La raíz cuadrada de un número  es otro número
es otro número  que elevado al cuadrado da
que elevado al cuadrado da  . Simbólicamente:
. Simbólicamente:
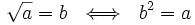
Al número  se le llama radicando y al número
se le llama radicando y al número  se le llama raíz.
se le llama raíz.
Raíz cuadrada de un número natural. Ejemplos. Obtención con la calculadora.
Raíz cuadrada de un número natural. Algoritmo para su cálculo.
Ejemplos de raíces cuadradas.
Raíces exactas y raíces enteras
Los cuadrados perfectos son los cuadrados de los números naturales:
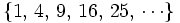
- Raíz cuadrada exacta es aquella cuyo radicando es un cuadrado perfecto.
- Raíz cuadrada inexacta es aquella cuyo radicando no es un cuadrado perfecto.
- Raíz cuadrada entera de un número es el mayor número natural cuyo cuadrado es menor o igual que dicho número. Se llama resto de la raíz cuadrada entera de un número a la diferencia entre dicho número y el cuadrado de su raíz cuadrada entera.
- La raíz cuadrada de 16 es exacta y su valor es 4, porque 16 es un cuadrado perfecto:
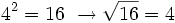
- La raíz cuadrada de 26 no es exacta y su raíz cuadrada entera es 5, porque:
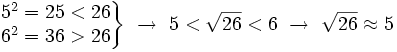
Nota: El símbolo 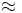 significa "aproximadamente igual".
significa "aproximadamente igual".
- Raíces cuadradas sencillas.
- Raíces cuadradas exactas y no exactas. Cálculo por exceso y por defecto.
- Ráices enteras y resto.
4 ejemplos.
Tutorial que explica el cálculo de la raíz cuadrada entera y su resto.
Halla 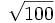 .
.
Tutorial que explica qué son los cuadrados perfectos y pone ejemplos con números menores que 100.
Tutorial que explica qué son los cuadrados perfectos y pone ejemplos con números mayores que 100.
Tutorial que explica qué son los cuadrados perfectos. La segunda parte del tutorial requiere conocer la descomposición en factores primos.
Practica con las raíces cuadradas exactas.
Practica con las raíces cuadradas enteras.
Actividad para que aprendas los cuadrados perfectos.
Raíces cuadradas de cuadrados perfectos.
Raíces cuadradas factorizando.
Raíces cuadradas exactas.
Ejercicios de autoevaluación sobre raíces cuadradas de números naturales.
Ejercicios de autoevaluación sobre raíces cuadradas exactas.
Ejercicios de autoevaluación sobre raíces cuadradas enteras.
Juego de tres en raya matemático para practicar las raíces cuadradas.
Cálculo de la raíz cuadrada por tanteo
Calcular una ráiz cuadrada por tanteo consiste en ir probando con distintos números, viendo si sus cuadrados son menores, mayores o iguales que el radicando, hasta averiguar entre qué dos cuadrados perfectos se encuentra el radicando.
Cálculo de la raíz cuadrada de un número usando el método de tanteo. Ejemplos.
|
Actividad: Raíces cuadradas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Algoritmo de la raíz cuadrada
Cálculo de la raíz cuadrada de un número natural usando el algoritmo. Ejemplos.
Raíces de números enteros. Algoritmo.
Cómo se calculan las raíces cuadradas. Algoritmo para calcular las raíces cuadradas, paso a paso.
Ejemplos de cálculo de raíces cuadradas exactas de un número natural usando el algoritmo.
Ejemplos de cálculo de raíces cuadradas enteras de un número natural usando el algoritmo.
Calcula: 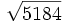
Calcula: 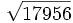
Calcula: 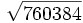
Actividades para aprender a calcular raíces cuadradas mediante el algoritmo.
En esta escena podrás practicar con el algoritmo de la raíz cuadrada.
Actividades para aprender a calcular raíces cuadradas mediante el algoritmo.
Ejercicios resueltos sobre el cálculo de raíces cuadradas usando el algoritmo.
Jerarquía de las operaciones con naturales
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Efectúa las siguientes operaciones: 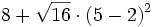
- Los paréntesis:
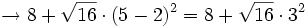
- Las potencias y las raíces:
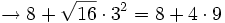
- Las multiplicaciones y divisiones:
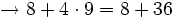
- Las sumas y restas:
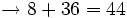
Aprende el orden en que han de hacerse las distintas operaciones con números naturales: sumas, restas, multiplicaciones, divisiones, potencias, raíces, paréntesis. Ejemplos.
Aprende el orden en que han de hacerse las distintas operaciones con números naturales.
Aprende el orden en que han de hacerse las distintas operaciones con números naturales.
¿Cuánto es 6÷2(1+2)? ¿9 ó 1?
En esta escena podrás practicar las operaciones con números naturales: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis, simples o dobles.
Ejercicios de autoevaluación sobre operaciones combinadas con números naturales.
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |
Raíz cuadrada
|
Calculadora: Raíz cuadrada |
Ejercicios y problemas
Descomposición de un número en sus distintas unidades
Problemas resueltos sobre números naturales
Autoevaluación sobre números naturales.
Amplia tus conocimientos sobre números naturales.
Control para enviar a tu profesor por correo.
Ejercicios sobre potencias y raíces cuadradas.
Test sobre potencias y raíces cuadradas.
Test sobre potencias y raíces cuadradas.
|
Ejercicios 1. Calcula:
Solución: a) 20 b) 48 c) 16 d) 30 2. Simplifica:
Solución: a) 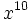 b) b) 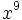 c) c) 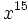 3. Simplifica:
Solución: a) 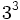 b) b) 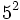 c) c) 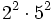 4. Extrae factor común:
Solución: a) 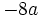 b) b) 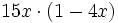 c) c) 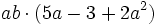 |
|
Problemas
1. Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división)
2. Una empresa compra una máquina de café por 6.000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio mensual le ha aportado la máquina?
Solución: 214 € |

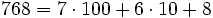
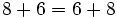
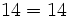
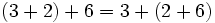
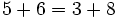
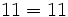
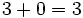
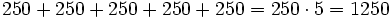 €
€
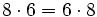
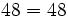
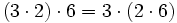

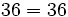
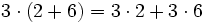
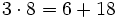
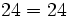
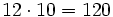
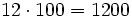
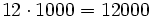
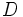 y
y 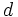 dos números naturales, con
dos números naturales, con 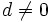 .
.
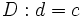
 , cociente.
, cociente.
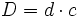 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 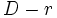 entre
entre 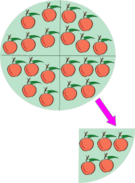
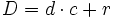

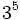 .
.
 .
.
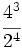
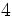


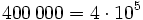
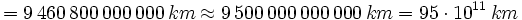
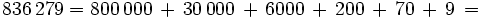
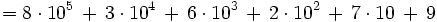
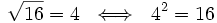
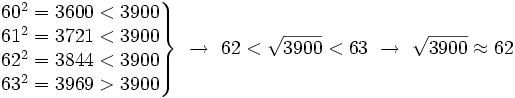 (sería la raíz entera de 3900)
(sería la raíz entera de 3900)
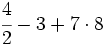
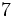
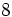
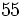
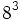
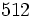
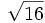
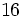
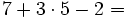
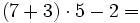
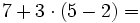
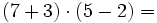
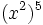 b)
b) 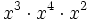 c)
c) 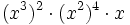
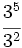 b)
b)  c)
c) 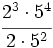
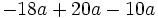 b)
b) 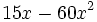 c)
c)