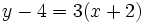Plantilla:Ecuación punto-pendiente de una recta
De Wikipedia
Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado:
Ecuación punto-pendiente
Sea 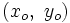 un punto de una recta y
un punto de una recta y  su pendiente, entonces su ecuación viene dada por:
su pendiente, entonces su ecuación viene dada por:
|
|
expresión que se denomina ecuación punto-pendiente de la recta.
Para comprobar que esta es la ecuación de la recta, comprobaremos que su pendiente es  y que pasa por el punto dado
y que pasa por el punto dado 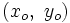 .
En efecto:
.
En efecto:
- Si desarrollamos la expresión de la ecuación punto-pendiente, se obtiene:
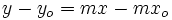
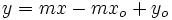
de donde se observa que el coeficiente e la x es  , y por tanto, la pendiente de la recta.
, y por tanto, la pendiente de la recta.
- Si sustituimos el punto
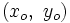 en la ecuación punto-pendiente, es decir, hacemos
en la ecuación punto-pendiente, es decir, hacemos 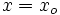 e
e 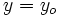 , se obtiene
, se obtiene
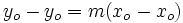
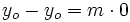
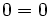
Ejemplo: Ecuación punto-pendiente
Halla la ecuación punto-pendiente de la recta que pasa por el punto (-2, 4) y tiene pendiente 3.
En la ecuación punto-pendiente:
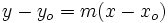
sustituimos 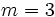 ,
, 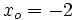 ,
, 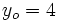 , obteniendo:
, obteniendo:
|
|
Introducción a la forma punto-pendiente de la ecuación de la recta.
Determina la ecuación general de la recta que pasa por el punto (-2,3) y es paralela a la recta 2x-3y=0.
Halla la ecuación de la recta que pasa por el origen de coordenadas y es paralela a al recta de ecuación 2x-y+3=0.
Actividades en las que aprenderás obtener la ecuación punto-pendiente de una recta.
En esta escena podrás practicar el cálculo de la ecuación de la recta con una cierta pendiente y que pasa por un punto dado.