Plantilla:Fenómenos que crecen de forma exponencial
De Wikipedia
Tabla de contenidos |
El crecimiento exponencial
La expresión crecimiento exponencial se aplica a una magnitud tal que varía en el tiempo de acuerdo a la ecuación: 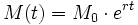
[editar] El modelo exponencialUn caso particular de crecimiento exponencial es el llamado modelo exponencial: El modelo exponencial es un modelo demográfico y ecológico para representar el crecimiento de las poblaciones y la difusión epidémica de un rasgo entre una población, basado en el crecimiento exponencial. Su ecuación es como la del crecicmiento exponencial 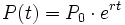 donde |
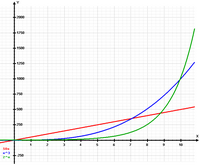
Algunos fenómenos que pueden ser descritos por un crecimiento exponencial, al menos durante un cierto intervalo de tiempo, son:
- El número de células de un embrión mientras se desarrolla en el útero materno.
- En una economía sin trastornos, los precios crecen exponencialmente, donde la tasa coincide con el índice de inflación.
- El crecicmiento de un capital a interés compuesto en un periodo de tiempo con amortizaciones periódicas.
- El crecicmiento de un capital a interés continuo (interés compuesto con amortizaciones instantáneas) en un periodo de tiempo.
- El número de contraseñas posibles con n dígitos crece exponencialmente con n.
- El número de bacterias que se reproducen por fisión binaria.
- El número de miembros en poblaciones de ecosistemas cuando carecen de predador y los recursos son ilimitados (no existe competencia intraespecífica).
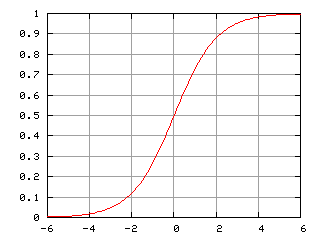
La función logística
La función logística, curva logística o curva en forma de S es una función matemática que aparece en diversos modelos de crecimiento de poblaciones, propagación de enfermedades epidémicas y difusión en redes sociales. Dicha función constituye un refinamiento del modelo exponencial para el crecimiento de una magnitud. Su gráfica pertenece al conjunto de las funciones sigmoideas.
El estudio inicial de crecimiento es aproximadamente exponencial; al cabo de un tiempo, aparece la competencia entre algunos miembros de la población por algún recurso crítico y la tasa de crecimiento disminuye; finalmente, en la madurez, el crecimiento se detiene.
La función logística simple se define mediante la expresión matemática:
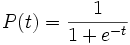
donde la variable P puede ser considerada o denotada como población, donde e es la constante de Euler (númerto e) y la variable t puede ser considerada el tiempo.
En su forma más general, la función logística se define por la fórmula matemática:
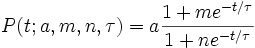
para parámetros reales a, m, n, y τ. Estas funciones tienen un campo de aplicación muy amplio, desde la biología a la economía.
Como ejemplo tenemos el desarrollo embrionario. En el desarrollo de un embrión, el óvulo fecundado comienza a dividirse y el número de células empieza a crecer: 1, 2, 4, 8, 16, 32, 64, etc. Éste es un crecimiento exponencial. Pero el feto sólo puede crecer hasta un tamaño que el útero pueda soportar; así, otros factores comienzan a disminuir el incremento del número de células, y la tasa de crecimiento disminuye. Después de un tiempo, el niño nace y continúa creciendo. Finalmente, el número de células se estabiliza y la estatura del individuo se hace constante. Se ha alcanzado la madurez, en la que el crecimiento se detiene.
La ecuación Verhulst y la catástrofe malthusiana
Una típica aplicación de la ecuación logística es un modelo común del crecimiento poblacional según el cual:
- La tasa de reproducción es proporcional a la población existente.
- La tasa de reproducción es proporcional a la cantidad de recursos disponibles.
El segundo término modela, por tanto, la competición por los recursos disponibles, que tiende a limitar el crecimiento poblacional.
Su ecuación viene dada por:
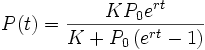
donde la constante 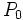 es la población inicial, la constante
es la población inicial, la constante  define la tasa de crecimiento y
define la tasa de crecimiento y 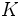 es la capacidad de persistencia o capacidad de carga. La capacidad de carga de una especie biológica en un ambiente es el tamaño máximo de población que el ambiente puede soportar indefinidamente en un periodo determinado, teniendo en cuenta el alimento, agua, hábitat, y otros elementos necesarios disponibles en ese ambiente.
es la capacidad de persistencia o capacidad de carga. La capacidad de carga de una especie biológica en un ambiente es el tamaño máximo de población que el ambiente puede soportar indefinidamente en un periodo determinado, teniendo en cuenta el alimento, agua, hábitat, y otros elementos necesarios disponibles en ese ambiente.
La ecuación Verhulst fue publicada por primera vez por Pierre François Verhulst en 1838 después de haber leído el "Ensayo sobre el principio de población" del demógrafo y economista político conservador Thomas Malthus. En este ensayo Malthus expone lo que se pasará a conocer como "la catástrofe malthusiana", una visión pesimista del crecimiento de población. Las tesis de Malthus aunque desajustadas a los hechos, tuvieron gran influencia política. Malthus llegó a afirmar que el crecimiento de la población libre de contenciones era un crecimiento exponencial, mientras que la producción de alimentos según su argumento era un crecimiento lineal. Puesto que la tasa de crecimiento de la población era más acelerada que la de alimentos a partir de un cierto umbral de población, Malthus pronosticó que habría una escasez de alimentos y una gran hambruna hacia mediados del siglo XIX. La gran hambruna predicha por Malthus jamás se produjo mostrando que los presupuestos lógicos de Malthus eran simplistas y en ocasiones hasta erróneos.
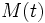 es valor de la magnitud en el instante
es valor de la magnitud en el instante 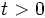 .
.
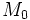 es el valor inicial de la variable, valor en
es el valor inicial de la variable, valor en 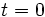 , cuando empezamos a medirla.
, cuando empezamos a medirla.
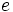 = 2,718281828459...
= 2,718281828459...
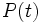 es el tamaño de la población en un instante t;
es el tamaño de la población en un instante t;