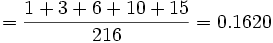Plantilla:Ley de laplace

De Wikipedia

El matemático francés Laplace da la siguiente definición de probabilidad para el caso en el que los sucesos elementales del espacio muestral sean equiprobables. Este resultado se conoce como ley o regla de Laplace.

Regla de Laplace:

En el caso de que todos los sucesos elementales del espacio muestral sean equiprobables, Laplace define la probabilidad del suceso A como el cociente entre el número de resultados favorables a que ocurra el suceso A en el experimento y el número de resultados posibles del experimento.

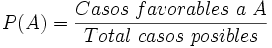
$P(A)= \frac{Casos\ favorables\ a\ A} {Total\ casos\ posibles}$

Se trata, por tanto, de un número comprendido entre 0 y 1.

Ejemplo: Regla de Laplace

En una baraja de 40 cartas, ¿cuál es la probabilidad de " salir AS"?, ¿Y de "salir ORO"?

Solución:

$P(AS)=\cfrac{n^\circ \ de \ ases}{n^\circ \ total \ de \ cartas}=\cfrac{4}{40}=0.1$

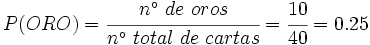
$P(ORO)=\cfrac{n^\circ \ de \ oros}{n^\circ \ total \ de \ cartas}=\cfrac{10}{40}=0.25$

Regla de Laplace Descripción:

Actividades en las que podrás aprender a utilizar la ley de Laplace.

Regla de Laplace

Tutorial 1 (5'52") Sinopsis:

Probabilidad de sucesos equiprobables. Ejemplos

Tutorial 2 (7'22") Sinopsis:

Cálculo de probabilidades usando la ley de Laplace
Ejemplos.

Tutorial 3 (13'37") Sinopsis:

La tercera parte de este videotutorial de 33'20" dura 14'00" y trata sobre:

Ley de Laplace.
Ejemplos.

Ejercicio 1 (5'28") Sinopsis:

Ejercicio 1: En el experimento de lanzar un dado de 6 caras, calcula la probabilidad de los siguientes sucesos:

a) Sacar el número 1.

b) Sacar un múltiplo de 3.

c) Sacar un número par.

d) Sacar el número 8.

e) Sacar un número del 1 al 6.

Ejercicio 2 (8'00") Sinopsis:

Ejercicio 2: En el experimento de lanzar un dado de 6 caras, se consideran los sucesos

A = Sacar un número impar.

B = Sacar un 2.

C = Sacar un 5.

Calcula las siguientes probabilidades:

a) 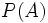$P(A)\;$

b) 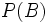$P(B)\;$

c) 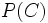$P(C)\;$

d) 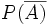$P(\ove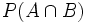rline{A)}\;$

e) $P(A \cap B)$ . ¿Son A y B incompatibles?

f) 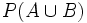$P(A \cup B)$

g) 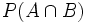$P(A \cap B)$ . ¿Son A y C incompatibles?

Ejercicios: Cálculo de probabilidades

Ejercicio 1. Si escogemos al azar dos números de teléfono y observamos la última cifra de cada uno, determina las probabilidades siguientes:

a) Que las dos cifras sean iguales

b) Que su suma sea 11

c) Que su suma sea mayor que 7 y menor que 13

Solución:

Solución 1:

El espacio muestral de este experimento está formado por los cien sucesos elementales: 00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, ..., 98, 99. Para cada suceso del enunciado calculamos sus casos favorables, aplicamos la regla de Laplace y obtenemos:

a) Los casos favorables son: 00, 11, 22, ..., 99. Son 10 casos. Así, la probabilidad de que las últimas cifras sean iguales es:

P(últimas cifras iguales) = 10/100 = 1/10 = 0.1

b) Los casos favorables a que la suma de las últimas cifras sea 11 son: 29, 38, 47, 56, 65, 74, 83 y 92. Por tanto,

P(últimas cifras suman once) = 8/100 = 0.08

c) Deben contarse los números de dos cifras cuya suma sea 8, 9, 10, 11 y 12. Haciendo un recuento ordenado, se obtienen 43 casos favorables. La probabilidad buscada es:

P(últimas cifras suman un valor mayor que 7 y menor que 13) = 43/100 = 0.43

Ejercicio 2. Se lanzan dos dados equilibrados con seis caras marcadas con los números del 1 al 6. Se pide:

a) Halla la probabilidad de que la suma de los valores que aparecen en la cara superior sea múltiplo de tres.

b) ¿Cuál es la probabilidad de que los valores obtenidos difieran en una cantidad mayor de dos?

Solución:

Solución 2:

El espacio muestral del experimento es:

E = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); ...; (6,6)}

y está formado por 36 sucesos elementales equiprobables. Constituyen el número de casos posibles del experimento.

Utilizando la regla de Laplace, calculamos las probabilidades de los sucesos que nos piden:

a) Si llamamos A al suceso "obtener una suma múltiplo de 3", los casos favorables al suceso A son:

A = {(1,2); (2,1); (1,5); (2,4); (3,3); (4,2); (5,1); (3,6); (4,5); (5,4); (6,3); (6,6)}.

Por tanto, P( A ) = 12/36 = 1/3

b) Si llamamos B al suceso "obtener unos valores que se diferencian en una cantidad mayor que dos", los casos favorables al suceso B son:

B = {(1,4); (4,1); (1,5); (5,1); (1,6); (6,1); (2,5); (5,2); (2,6); (6,2); (3,6);(6,3)}.

Por tanto, P( B ) = 12/36 = 1/3

Ejercicio 3. Se tiran tres dados al mismo tiempo. Encuentra la probabilidad de que:

a) La suma de los números aparecidos sea menor que 8.

b) La suma de los números sea mayor que 4 y menor que 8.

Solución:

Solución 3:

Los casos posibles de este experimento son las 216 ternas siguientes: 111, 112, 121, 211, ..., 665, 666.

Realizando un recuento ordenado de los casos favorables a los sucesos del enunciado, obtenemos las siguientes probabilidades:

a) P(suma de valores menor que 8) 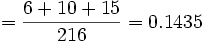$= \frac {1+3+6+10+15} {216}= 0.1620$

b) P(suma de valores mayor que 4 y menor que 8) $= \frac {6+10+15} {216}= 0.1435$

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Ley_de_laplace"

Plantilla:Ley de laplace

De Wikipedia

Vistas

Herramientas personales

Menú

Buscar

Herramientas