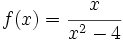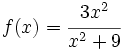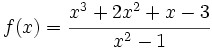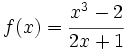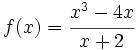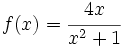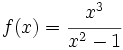Plantilla:Ramas infinitas de las funciones racionales
De Wikipedia
Proposición
Consideremos la función racional en la variable x, ya simplificada (es decir, si el numerador y el denominador tienen factores comunes, cosa que ocurre si se anulan simultáneamente en algún punto, factorizaremos y simplificaremos dichos factores):
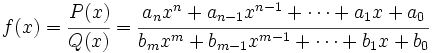
La función  (ya simplificada) tiene las siguientes ramas infinitas, si se da alguno de los siguientes casos:
(ya simplificada) tiene las siguientes ramas infinitas, si se da alguno de los siguientes casos:
- Asíntotas verticales:
- Si
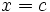 es una raíz de Q(x), entonces la recta
es una raíz de Q(x), entonces la recta 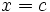 es una asíntota vertical de
es una asíntota vertical de  .
.
- Si
- Asíntotas horizontales:
- Si
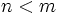 , entonces la recta
, entonces la recta 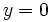 es una asíntota horizontal de
es una asíntota horizontal de  , tanto por
, tanto por  , como por
, como por  .
.
- Si
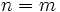 , entonces la recta
, entonces la recta 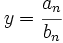 es una asíntota horizontal de
es una asíntota horizontal de  , tanto por
, tanto por  , como por
, como por  .
.
- Si
- Asíntotas oblicuas:
- Si
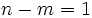 ,
,  tienen una asíntota oblicua, tanto por
tienen una asíntota oblicua, tanto por  , como por
, como por  . Dicha asíntota es igual al cociente de la división entre
. Dicha asíntota es igual al cociente de la división entre  y
y  .
.
- Si
- Ramas parabólicas:
- Si
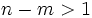 , entonces
, entonces  tiene una rama parabólica, tanto por
tiene una rama parabólica, tanto por  , como por
, como por  .
.
- Si
Obtén las asíntotas de la función 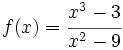
Obtén las asíntotas de la función 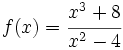
Obtén las asíntotas de las funciones:
Obtén las asíntotas de las funciones:
Estudio de las asíntotas de 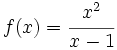 .
Hace un estudio detallado de la posición relativa de la curva respecto de la asíntota oblicua usando el método riguroso de límites.
.
Hace un estudio detallado de la posición relativa de la curva respecto de la asíntota oblicua usando el método riguroso de límites.
Lista de reproducción que consta de 12 vídeos sobre estudio de asíntotas de funciones racionales.
Ejercicios resueltos
Halla todas las ramas infinitas de las siguientes funciones:
- a)
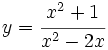 b)
b) 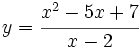 c)
c) 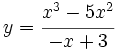
a) A.V.: x=0, x=2; A.H.: y=1
b) A.V.: x=2; A.O.: y=x-3
c) A.V.: x=3; R.I.
Haz uso de la siguiente escena de Geogebra para comprobar las soluciones:
En esta escena podrás representar funciones definidas en hasta 4 trozos.