Plantilla:Suma de ángulos
De Wikipedia
Dos o más ángulos pueden sumarse para formar otro. La operación suma de ángulos se realiza tanto gráficamente como analíticamente:
- La suma gráfica se realiza colocando los ángulos en posición de consecutivos, es decir, compartiendo el vértice y un lado, para dar lugar a otro ángulo que comprende a ambos.
- La suma analítica se realiza sumando las amplitudes de los ángulos para obtener la amplitud del ángulo resultante.
Suma de ángulos Descripción: Actividad en la que podrás ver como se suman ángulos gráficamente y de forma analítica en forma simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Suma de ángulos Descripción: Construcción gráfica de la suma de dos ángulos, con regla y compás.
Procedimiento
Para sumar analíticamente un ángulos en sexagesimal, en forma compleja:
- Sumamos cada una de las unidades del ángulo (grados, minutos y segundos).
- Si la suma de los segundos es superior a 60, la transformamos en minutos, y se la añadimos a los minutos.
- Si la suma de los minutos es superior a 60, la transformamos en grados, y se la añadimos a los grados.
Ejemplo: Suma de ángulos
Calcula la siguiente suma de ángulo en sexagesimal en forma compleja:
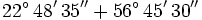
Solución:
Si sumamos por separado los grados, los minutos y los segundos, resulta:
22º 48' 35" + 56º 45' 30" _______________ 78º 93' 65"
Pero 65" equivalen a 1' (60") y 5", luego la suma se puede escribir así:
78º 94' 5"
De la misma forma, 94' equivalen a 1º (60') y 34'. Luego la suma es:
79º 34' 5"
Actividad 1 Descripción: Realiza en tu cuaderno las siguientes sumas de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" + 37º 42' 15"
- b) 125º 15' 30" + 24º 50' 40"
- c) 33º 33' 33" + 17º 43' 34"
Actividad 2 Descripción: Suma de ángulos en sexagesimal.
Tutorial (6'25") Sinopsis:Suma de ángulos en forma compleja.
Ejercicio 1 (3'37") Sinopsis: Calcula: (26º 42' 51") + (11º 30' 14")
Ejercicio 2 (2'48") Sinopsis: Calcula: (26º 14' 41") + (24º 59")
Ejercicio 3 (2'42") Sinopsis: Calcula: (38º 47') + (19º 54' 10")
