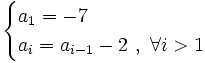Plantilla:Término general de una progresión aritmética
De Wikipedia
Término general de una progresión aritmética
El término general,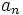 
, de una progresión aritmética de diferencia 
es:
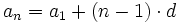
En efecto, de forma intuitiva:
........................
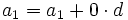
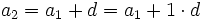
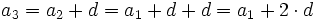
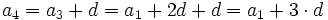
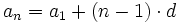
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
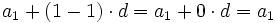
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
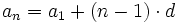. [1]Por ser una progresión aritmética cada término se obtiene sumando d al anterior término:
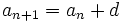[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n+ d \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 + (n-1) \cdot d + d =a_1 + ((n+1)-1) \cdot d](/wikipedia/images/math/7/4/4/744cf81c67660fb80f54db415de019dd.png)
Tutorial 1 (6´59") Sinopsis:- Definición de progresión aritmética.
- Término general
- Ejemplos
Tutorial 2 (21'54") Sinopsis:Tutorial en el que se explica y trabajan las progresiones aritméticas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Tutorial 3a (6´16") Sinopsis:Término general de una progresión aritmética: Obtención y ejemplos.
Tutorial 3b (5´34") Sinopsis:Término general de una progresión aritmética: Más ejemplos
Tutorial 3c (4´10") Sinopsis:Término general de una progresión aritmética a partir de términos intermedios.
Tutorial 4 (10´21") Sinopsis: - Definición de progresión aritmética.
- Ejemplos
- Término general
Ejercicio 1 (6´39") Sinopsis: - Una progresión aritmética tiene como término general
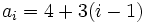, halla el término 
.
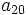- Halla el término
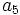de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Ejercicio 2 (7´08") Sinopsis: Halla el término general y la forma recursiva de las siguientes progresiones aritméticas:
- a) {-5, -3, -1, 1, ...}
- b) {100, 107, 114, 121, ...}
- c) {1, 3, 6, 10, ...}
Ejercicio 3 (9´49") Sinopsis: Halla el término general de las siguientes progresiones aritméticas:
- a) {12, 5, -2, -9, ...}
- b) {-100, -50, 0, 50, ...}
Ejercicio 4 (5´58") Sinopsis: Halla el término 100 de la siguiente progresión aritmética: {15, 9, 3, -3, ...}.
Ejercicio 5 (9´33") Sinopsis: Halla la forma recursiva de la progresión aritmética con término general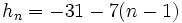 
Actividad 1 Descripción: Actividad de introducción a las fórmulas de sucesiones aritméticas.
Actividad 2 Descripción: Actividad para aprender a obtener el término general (fórmula explícita) de sucesiones aritméticas.
Actividad 3 Descripción: Actividades en las que aprenderás a obtener el término general de una progresión aritmética.
Actividad 4 Descripción: Convertir formas de sucesiones aritméticas, recursivas y explícitas.
Actividad 5 Descripción: Repaso de sucesiones aritméticas.
Autoevaluación 1 Descripción: Usa el término general de progresiones aritméticas.
Autoevaluación 2 Descripción: Obtén el término general (fórmula explícita) de sucesiones aritméticas.
Autoevaluación 3 Descripción: Encuentra el término general de una progresión aritmética dada.
Autoevaluación 4 Descripción: Convertir formas de sucesiones aritméticas, recursivas y explícitas.
