Plantilla:Ternas pitagóricas
De Wikipedia
- Se llaman ternas pitagóricas a las ternas de números naturales que verifican el teorema de Pitágoras.
- Las ternas cuyos tres números son primos entre sí, es decir, tales que m.c.d(a,b,c)=1, reciben el nombre de ternas pitagóricas primitivas.
- (3,4,5) es una terna pitagórica (52 = 32 + 42).
- También son ternas pitagóricas sus múltiplos: (6,8,10), (9,12,15), ... ,(3k,4k,5k) con
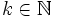 .
.
Las ternas pitagóricas. Ejemplos.
[editar]
Generando ternas pitagóricas
Proposición
Si 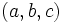 es una terna pitagórica entonces también lo es
es una terna pitagórica entonces también lo es 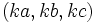 , con
, con 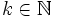 .
.
Demostración:
Sea (a,b,c) es una terna pitagórica. Se cumple:
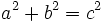 [1]
[1]Vamos a comprobar que (ka,kb,kc) también lo es y para ello veremos que también cumple el teorema de Pitágoras:
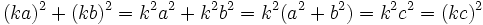
donde en el el penúltimo paso hemos utilizado la igualdad [1].
Por tanto, (ka,kb,kc) cumple el teorema de Pitágoras y es una terna pitagórica.En esta escena podrás ver como se generan ternas pitagóricas.
Proposición
Si 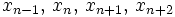 son cuatro términos cualesquiera de la sucesión de Fibonacci, entonces los siguientes números
son cuatro términos cualesquiera de la sucesión de Fibonacci, entonces los siguientes números
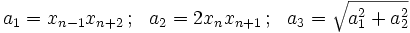
forman una terna pitagórica.
Demostración:
Se demuestra expresando los términos centrales de la subsucesión de Fibonacci, en función de los términos extremos y, luego, aplicando el teorema de Pitágoras para
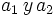 considerándolos como 'catetos'.
considerándolos como 'catetos'.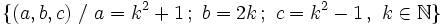 son ternas pitagóricas.
son ternas pitagóricas.
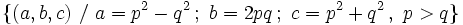 son ternas pitagóricas.
son ternas pitagóricas.

