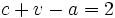Poliedros
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Poliedro
| El siguiente videotutorial resume los conceptos y resultados más importantes del tema:
Videotutorial que resume los conceptos y resultados más importantes del tema:
[editar] Definición de poliedroPoliedro es un cuerpo geométrico cerrado, limitado por caras poligonales. Las caras de un poliedro, al ser polígonos, no pueden ser curvas. Así, un cono, una esfera o un cilindro, no son poliedros. Definición de poliedro. Ejemplos. Actividades en la que podrás aprender lo que es un poliedro. |
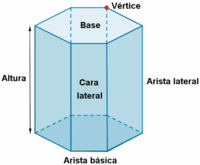
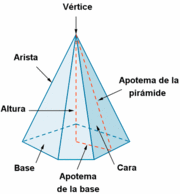
Elementos de un poliedro
- Caras: Polígonos que limitan al poliedro.
- Aristas: Segmentos intersección de las caras.
- Vértices: Puntos de intersección de las aristas.
Se llama orden de un vértice de un poliedro, al número de caras (o aristas) que concurren en él.
Definición de poliedro. Elementos.
Definición de poliedro. Elementos.
Actividad en la que deberás separar los cuerpos que son poliedros de los que no lo son.
Actividades en la que podrás estudiar los distintos elementos de un poliedro.
Definición de poliedro. Elementos. Relación de Euler.
Denominación de los poliedros
Los poliedros son denominados de acuerdo a su número de caras. Su designación se basa en el griego clásico.
| Nombre | Nº caras | Nombre | Nº caras | Nombre | Nº caras |
|---|---|---|---|---|---|
| tetraedro | 4 | tridecaedro | 13 | tetracontaedro | 40 |
| pentaedro | 5 | tetradecaedro | 14 | pentacontaedro | 50 |
| hexaedro | 6 | pentadecaedro | 15 | hexacontaedro | 60 |
| heptaedro | 7 | hexadecaedro | 16 | heptacontaedro | 70 |
| octaedro | 8 | heptadecaedro | 17 | octacontaedro | 80 |
| eneaedro | 9 | octadecaedro | 18 | eneacontaedro | 90 |
| decaedro | 10 | eneadecaedro | 19 | hectaedro | 100 |
| endecaedro | 11 | icosaedro | 20 | chiliedro | 1000 |
| dodecaedro | 12 | triacontaedro | 30 | miriedro | 10000 |
Tipos de poliedros
Prisma
Prisma: definición y elementos. Actividad en la que se presentan distintos tipos de prismas y en la que podrás ver sus elementos. | Elementos de un prisma
de http://calculo.cc |
Clasificación de los prismas
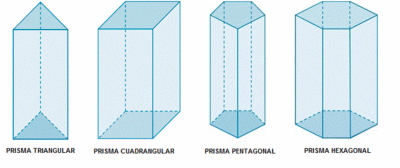
- Atendiendo a sus bases: En función del polígono de las bases, los prismas pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.
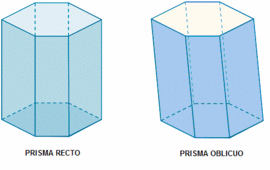
- Atendiendo a su inclinación: Si las caras laterales son perpendicualres a las bases (son rectángulos), el prisma es recto, si no , es oblicuo.
- Atendiendo a su regularidad: Un prisma es regular si su base es un polígono regular. En caso contrario es irregular. En una prisma regular, todas las aristas laterales son iguales y las caras laterales son rectángulos iguales
Clasificación de los prismas.
Dibuja un prisma de base pentagonal y recuenta sus caras, vértices y aristas.
Actividad en la que se presentan distintos tipos de prismas regulares.
Actividad interactiva en la que aprenderás los elementos y la clasificación de los prismas regulares.
Atendiendo a su inclinación
de http://calculo.cc | Atendiendo a su base
de http://calculo.cc |
Paralelepípedos
- Los paralelepípedos son prismas en los que todas sus caras son paralelogramos.
- Las bases han de ser paralelogramos y por tanto los paralelepípedos son prismas cuadrangulares.
- Entre ellos destacamos cuatro en particular:
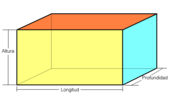
- Ortoedro: sus caras son rectángulos.
- Cubo: sus caras son cuadrados.
- Romboedro: Todas sus caras son rombos.
- Romboiedro: Todas sus caras son romboides.
Actividad en la que podrás conocer los paralelepípedos y sus distintos tipos.
Ortoedro
| Ortoedro
|
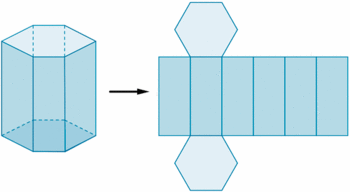
Desarrollo plano de un prisma
Si representamos en un plano todas las caras de un prisma, de forma contigua, obtenemos lo que se denomina desarrollo plano del prisma.
Fíjate en el siguiente prisma hexagonal. Si cortásemos adecuadamente el prisma, siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura.
de http://calculo.cc
Actividad en la que se presentan los desarrollos planos de distintos prismas rectos regulares.
Dibuja el desarrollo plano del siguiente poliedro.
Actividades
Ejecicios de autoevaluación sobre los prismas.
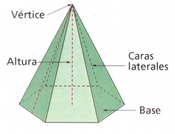
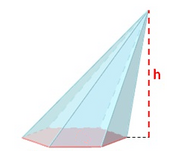
Pirámide
Actividad en la que se presenta la pirámide y sus elementos. Pirámide: definición y elementos. | Piramide recta
|
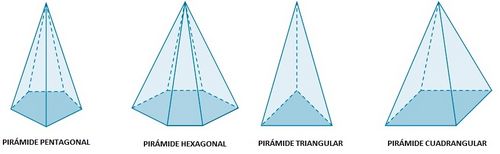
Clasificación de las pirámides
| Pirámide oblicua
de http://universoformulas.com |
Clasificación de las pirámides. Actividad en la que se presentan distintos tipos de pirámides regulares. Clasificación de las pirámides atendiendo a su base
de http://calculo.cc En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. Definiciones, elementos y propiedades. | Elementos de una pirámide regular
de http://calculo.cc |
Dibuja un pirámide de base cuadrangular regular y una pirámide de base triangular irregulr. Recuenta sus caras, vértices y aristas.
Ejecicios de autoevaluación sobre la pirámide.
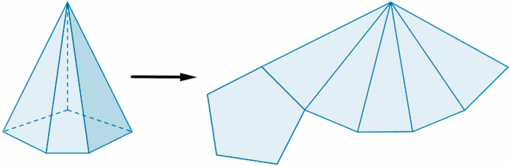
Desarrollo plano de una pirámide
Si representamos en un plano todas las caras de una pirámide, de forma contigua, obtenemos lo que se denomina desarrollo plano de la pirámide.
Fíjate en la siguiente pirámide pentagonal. Si la cortásemos adecuadamente, siguiendo ciertas aristas, podríamos desplegarla como se muestra en la siguiente figura.
de http://calculo.cc
Actividad en la que podrás ver el desarrollo plano de distintas pirámides rectas regulares.
Dibuja el desarrollo plano del siguiente poliedro.
Poliedros simples
Poliedro simple es aquel que no tiene orificios. Un poliedro simple es el que podría hincharse o deformarse (si el material lo permitiera) hasta formar una esfera. En la imagen de la derecha tienes un poliedro que no es simple. Al hincharlo, se transforma en un flotador, en vez de en una esfera. Este poliedro es muy especial porque forma un anillo o aro, es decir tiene una ventana que le atraviesa. Tiene 14 vértices y 21 aristas. |
Poliedros regulares
- Poliedro regular es aquel que cumple:
- Sus caras son polígonos regulares iguales.
- Todos los vértices tienen el mismo orden (en todos ellos concurren el mismo número de aristas).
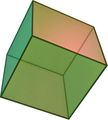
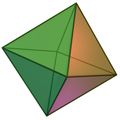
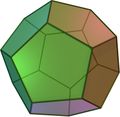
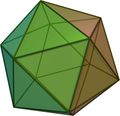
- Sólo hay cinco poliedros regulares, los llamados sólidos platónicos: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
Videotutorial.
Videotutorial.
Videotutorial.
El tetraedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El hexaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
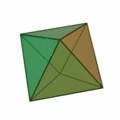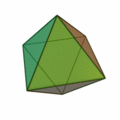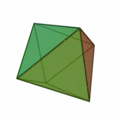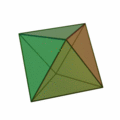
El octaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
Calcula el área de un dodecaedro de 6 cm de arista y 4 cm de radio.
En esta escena podrás ver y rotar los poliedros regulares.
Actividad en la que se presentan los 5 poliedros regulares y se hace un recuento de sus elementos.
Actividad interactiva sobre poliedros regulares.
Actividades sobre el tetraedro.
Actividades sobre el octaaedro.
Actividades sobre el hexaedro o cubo.
Actividades sobre el dodecaedro.
Ejecicios de autoevaluación sobre poliedros regulares.
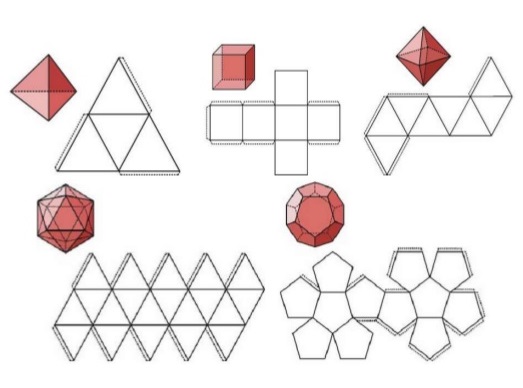
Desarrollo plano de los poliedros regulares
Si representamos en un plano todas las caras de un poliedro, de forma contigua, obtenemos lo que se denomina desarrollo plano del poliedro.
Si cortásemos adecuadamente cada uno de los poliedros regulares, siguiendo ciertas aristas, podríamos desplegarlos como se muestra en la imagen adjunta.
Actividad en la que se muestra el desarrollo plano de los 5 poliedros regulares.
Recursos
{{{descripcion}}}
{{{descripcion}}}
{{{descripcion}}}
{{{descripcion}}}
Actividades
Actividades sobre los elementos de prismas y pirámides.
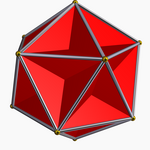
Poliedros convexos y cóncavos
- Un poliedro es convexo si al dados dos puntos cualesquiera del poliedro, el segmento que los une es interior al poliedro. En el caso de que dicho segmento se salga del cuerpo se dice el poliedro es cóncavo.
Son poliedros cóncavos, por ejemplo, los poliedros de Kepler-Poinsot:
En esta escena podrás ver y rotar los cuatro poliedros de Kepler-Poinsot.
Poliedros duales
Dado un poliedro, al unir mediante segmentos los centros de cada dos caras contiguas, se obtiene otro poliedro que se llama el poliedro dual del dado.
 Poliedros regulares y sus dualesEl cubo y el octaedro son duales.El dodecaedro y el icosaedro son duales.El tetraedro es dual de sí mismo
Poliedros regulares y sus dualesEl cubo y el octaedro son duales.El dodecaedro y el icosaedro son duales.El tetraedro es dual de sí mismoEn esta escena podrás comprobar cuales son los duales de los poliedros regulares.
Construccción del poliedro dual del cubo
Actividades sobre el poliedro dual del tetraedro.
Actividades sobre el poliedro dual del cubo.
Actividades sobre el poliedro dual del dodecaedro.
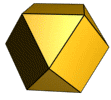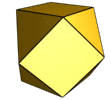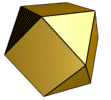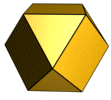
Poliedros semiregulares
Se llama poliedro semiregular a aquel cuyas caras son polígonos regulares de dos o más tipos y tal que en todos los vértices concurren los mismos polígonos.
Son poliedros semiregulares:
Fórmula de Euler
En un poliedro simple, se cumple la siguiente relación, llamada fórmula de Euler :
|
|
siendo 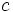 , el número de caras,
, el número de caras, 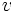 , el número de vértices y
, el número de vértices y 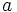 , el número de aristas.
, el número de aristas.
Ejemplo: Fórmula de Euler
Comprueba la fórmula de Euler en los cinco poliedros regulares, e indica el orden de sus vértices.
Puedes ayudarte de la siguiente escena:
En esta escena podrás comprobar la fórmula de Euler para los 5 poliedros regulares.
Videotutorial.
Comprueba si se cumple la fórmula de Euler en los siguientes poliedros
Comprueba la fórmula de Euler en el octaedro.
Actividad en la que podrás comprobar la fórmula de Euler en distintos poliedros.
Actividad en la que podrás comprobar la fórmula de Euler en distintos poliedros.
Ejecicios de autoevaluación sobre la fórmula de Euler.
Poliedros truncados
Un poliedro truncado es aquel en el que se ha suprimido un vértice cortándolo mediante un plano.
Poliedros regulares truncados
Algunos ejemplos los podemos encontrar entre los llamados sólidos arquimedianos. He aquí dos de ellos:
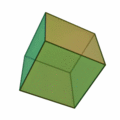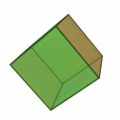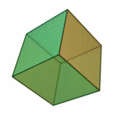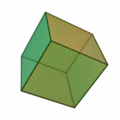
- Cuboctaedro: Se obtiene al truncar todos los vértices de un cubo mediante planos que pasan por los puntos medios de las aristas adyacentes. Es un poliedro semiregular con 6 caras que son cuadrados y 8 caras que son triángulos equiláteros.
- Icosidodecaedro: Se obtiene al truncar todos los vértices de un dodecaedro regular mediante planos que pasan por los puntos medios de las aristas adyacentes. Es un poliedro semiregular con 6 caras que son cuadrados y 8 caras que son triángulos equiláteros.
Otros ejemplos, que también son sólidos arquimedianosson:
El cubo truncado, el tetraedro truncado, el octaedro truncado, el dodecaedro truncado y el icosaedro truncado son el resultado de truncar los cinco poliedros regulares o sólidos platónicos mediante planos que un punto adecuado de la arista (que no es su punto medio), de manera que se obtengan poliedros semiregulares.